8.2. Нормирование требований к надежности цепи поставок

Классическая процессная модель управления цепью поставок по критерию минимума затрат при независимости процессов и заданным требованием к безотказности имеет вид

(8.9)

при ограничениях

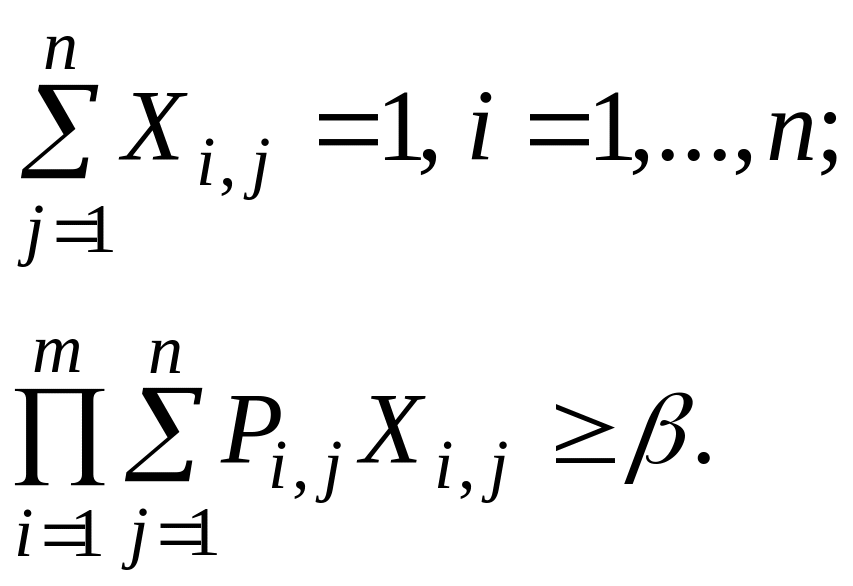
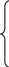(8.10)

где m – количество процессов; – количество стратегий; – количество возможных вариантов (стратегий) реализации i-го процесса; – затраты на i-й процесс в ЦП при реализации j-ой стратегии, – матрица затрат на процессы; β – задаваемая (требуемая) безотказность цепи поставок (вероятность безотказной работы); – вероятность безотказной реализации j-ой стратегии в i-м процессе, – матрица вероятностей безотказной работы; – бинарная переменная (переменная выбора), принимающая значение либо 0, либо 1.

Сложностью использования модели (8.9)-(8.10) является необходимость статистических исследований для получения объективных оценок матрицы . В то же время, при проектировании цепи поставок необходимо решать задачи выбора поставщиков услуг (т.е. процессов), исходя из требований конечного потребителя к надежности поставки β. Иными словами, возникает задача нормирования требований к процессной безотказности [68]. Рассмотрим алгоритм решения этой задачи, предложенный в работе [74], полагая процессы независимыми, а потоки отказов простейшими.

Из основного уравнения надежности имеем

(8.11)

откуда

(8.12)

где – интенсивность потока отказов цепи поставок; – значение фактора риска (время, объем и т.п.) при уровне безотказности β.

При отсутствии в цепи поставок процессов с доминирующей интенсивностью отказов можно положить

(8.13)

где – интенсивность отказов i-го процесса при j-ой стратегии реализации; – весовой коэффициент вклада j-ой стратегии i-го процесса в общую интенсивность отказов цепи поставок.

С учетом (4.13) получим следующее выражение для вероятности безотказной реализации j-ой стратегии в i-м процессе

(8.14)

Остается определить матрицу весовых коэффициентов . Очевидно, требование к надежности процесса должно быть тем выше, чем больший ущерб наносит отказ при его реализации. Ущерб может измеряться издержками восстановления процесса, потерями в реализации товара и т.п. Например, издержки можно оценить через потери на обороте и тарифах по формуле

где Q – оборот; d – продажная цена; δ, ε – потери на обороте и цене в % соответственно.

Весовые коэффициенты в этом случае связаны с издержками обратно пропорциональной зависимостью и определяются по формуле

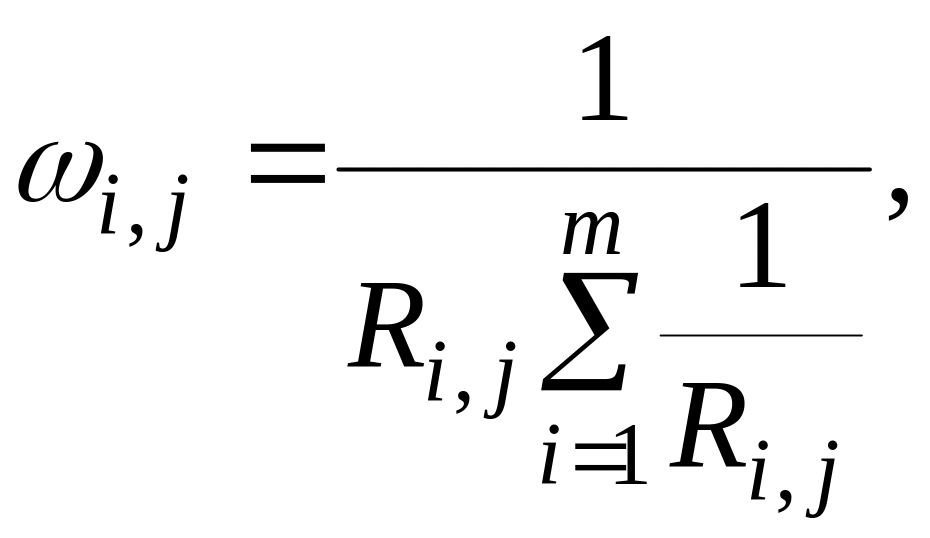(8.15)

где – издержки, связанные с отказом при реализации j-ой стратегии i-го процесса.

Полный алгоритм решения задачи математического программирования (8.9)-(8.10) с учетом нормирования требований к надежности процессов выглядит следующим образом

(8.9)

при ограничениях

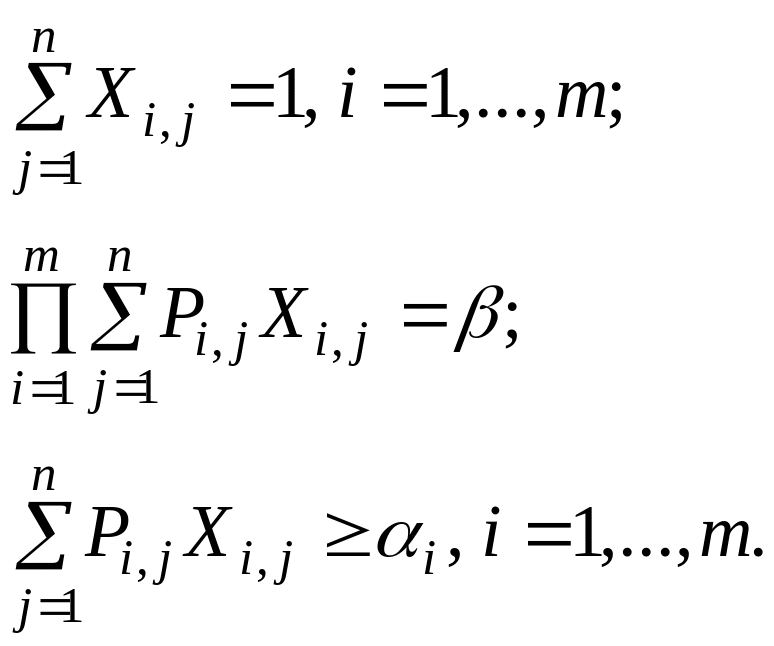
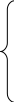(8.16)

где – ограничение на безотказность i-го процесса.

Отличием от классической модели (8.9)-(8.10) является требование равенства во втором ограничении в системе (8.16) и наличие дополнительного ограничения на надежность отдельных процессов в цепи поставок – третье ограничение в системе (8.16). Решение находится в виде ненулевого вектора из матрицы .

Таким образом, решение данной задачи математического программирования позволит выбрать поставщиков услуг (или процессов), исходя из требований конечного потребителя к надежности поставки β.

Пример 8.4. При заданной безотказности 5-ти процессной модели цепи поставок β = 0,85 и ограничениях на безотказность процессов α ≥ 0,95 необходимо выбрать оптимальные стратегии их реализации и определить соответствующие этим стратегиям требования к надежности поставляемых посредниками процессов. Затраты и связанные с отказами издержки заданы в виде матриц:

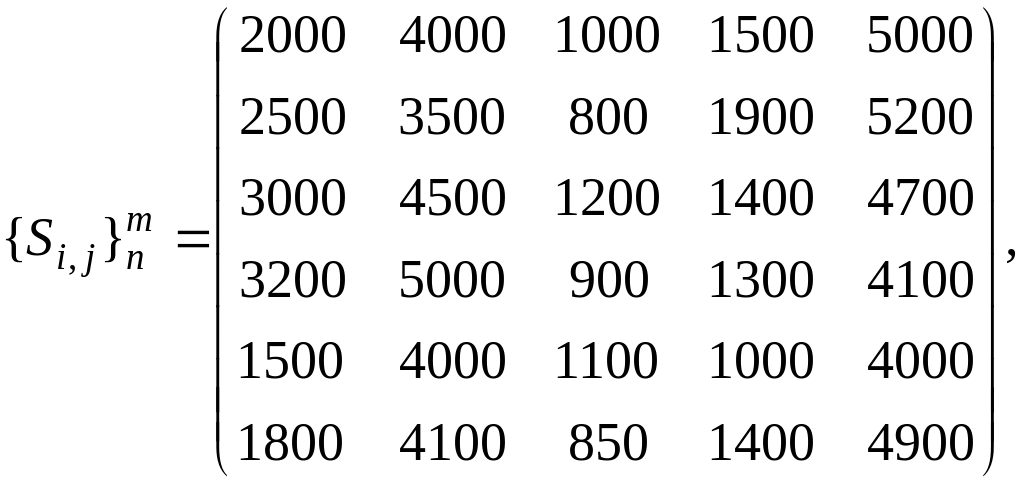
Имеем задачу математического программирования с бинарными переменными, для решения которой используем математическое программное обеспечение с функцией оптимизации.

После оптимизации данной модели получим следующее решение:

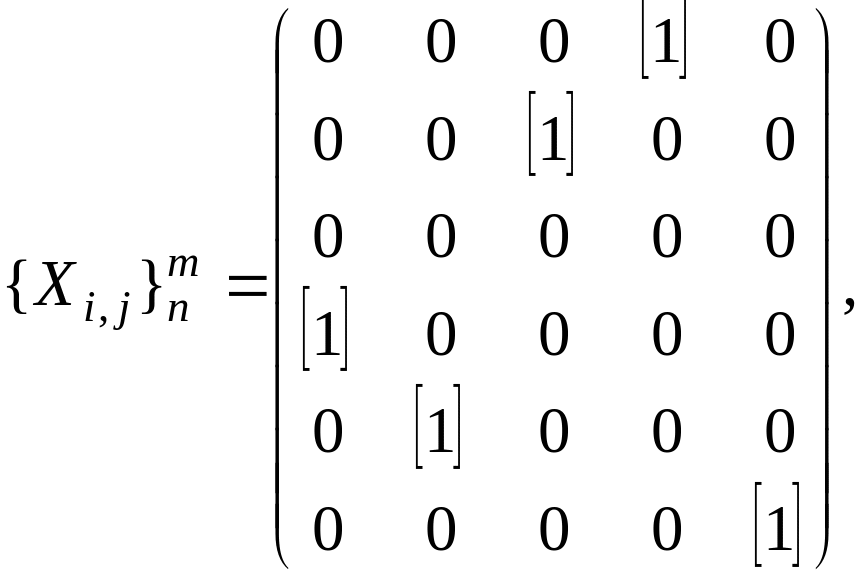
минимальные суммарные затраты обеспечиваются при использовании стратегий (выделены в матрице бинарных переменных) X_1,4=1; X_2,3=1; X_4,1=1; X_5,2=1; X_6,5=1. При этом должна быть обеспечена надежность процессов не ниже P_j = (0,958; 0,980; 0,954; 0,960; 0,987).

Таким образом, в 5-ти процессной модели цепи поставок, исходя из требований конечного потребителя к надежности поставки β = 0,85 и при и ограничениях на безотказность процессов α ≥ 0,95, необходимо обеспечить надежность: процесса «Plan» на уровне P₁=0,958; процесса «Source» – P₂=0,980; процесса «Make» – P₃=0,954; процесса «Deliver» – P₄=0,960; процесса «Return» – P₅=0,987.