1. Предмет и задачи матпро. Постановка общей задачи МП. Матпро – это раздел матем-ки, в кот-ой разраб-ся числовые м-ды решения многомерных задач с ограничениями. Чтобы решить задачу матем. м-дами необходимо составить модель. Мат.модель – это с-ма матем. выражений, которая описывает хар-ки изучаемого объекта и взаимосвязи м/у ними. Матпро включает: ленейное пргр-е, динамическое прогр-е, целочисленное прогр-е, дробнолинейное прогр-е и т.д. Постановкой общей задачи МП: определить значение неизв-ых х1,х2,…хn, при которых выпол-ся ограничения gi(x1,x2,….xn) (<=,=, >=) bi(i=1,m)(1) и доставляется экстремум функции Z=f(x1,x2,…xn) –extr-(2) целевая функция или функция цели. Значение переменных (х1,х2,…хn) наз-ся решением задачи или планом. План удовлетворяющий ограничениям (1) наз-ся допустимым. Допустимый план, при котором значения достигают экстремума наз-ся оптимальным. Задачи МП: определение оптимального плана, опред-е оптимального объема выпуска продукции, опред-е оптим-го сочитания посевов с/хоз-ых культур, формир-е оптим-го пакета активов, максимиз-щий прибыль банка и т.д.

Экономические примеры задач, решаемых методами МП. Компания имеет 2 склада и 3 оптовых покупателей. Запасы на складах составляют 120 и 180 тыс.ед., а потребность покупателей 70,140,90тыс.ед. Стоимость транспортировки 1тысячи продукции приведена в матрице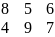 . Определить план при транспортировки, при котором суммарные затраты минимальные. А1, А2 –склад, В1,В2,В3 –потребители. Обозначим ч/з хij-количество продукции, перевозимое со склада Аi(i=1,2) потребителю Bj(j=1,3). Затраты на транспортировку могут быть описаны функцией. f=8x11+5x12+6x13+4x21+9x22+7x23 –min

{x11+x12+x13=120

{x21+x22+x23=180

{x11+x21=7 xiJ>=0 (i=1,2) (j=1,3)

{x12+x2=140

{x13+x23=90

Предприятие может производить 2 вида продукции(П1,П2), используя для этого 3вида ресурсов сырье, оборудование и труд.

ресурс	Росход ресурсов на ед.прод.		Кол-во ресурсов
	П1	П2
Сырье,кг	1	3		210
Фонд времени работы оборудования ст/час	3	2		210
Труд, чел/час	3	1		180
Прибыль от реализации ед.прод.	35	49

Определить оптим. план выпуска продукции. Обозначим х1,х2 количество продукции П1 и П2 в оптимальном плане. Прибыль опишется функцией: f= 35x1+49x2 – max

1x1+3x2<=210}

3x1+2x2<=210}

3x1+x2<=180 }

x1>=0,x2>=0

2. Различные формы записи злп (общая, каноническая, симметрическая)

Задачи МП: определение оптимального плана, опред-е оптимального объема выпуска продукции, опред-е оптим-го сочитания посевов с/хоз-ых культур, формир-е оптим-го пакета активов, максимиз-щий прибыль банка и т.д.

Общей ЗЛП называют задачу максимизации (минимизации) линейной функции f=Σcj*xj-max(min) (1) при линейных ограничениях ∑aij *xj{=<,=,>=}bi (i=1,n) (2) при условии xj>=0(j=1,n1), xj-произвольное (j=n1+1,n )(3) где cj,aij, bi-постоянные числа.

Симметрической формой записи ЗЛП наз-ся задача максимизации функции (1) при линейных ограничениях в неравенствах со знаком < либо = и не отрицательных переменных и задача минимизации функции (1) при линейных ограничениях в неравенствах со знаком > либо = и неотрицательных переменных. Канонической формой записи ЗЛП наз-ся задача максимальной функции (1) при линейных ограничениях равенствах и неотрицательных переменных. Любая другая форма называется смешенной.

min f(x) = -max(-f(x))

Преобразование нерав-ва в уравнение и наоборот осущ-ся на основе Леммы: всякому решению х1…хn нерав-ва a1x1+…+anxn<=b (5)соответствует вполне определенное решение х1…хn, xn+1 уравненияa1x1+…+anxn+xn+1=b (6) при условии что хn+1>=0(7) и наоборот. Всякому решению x1…xn,xn+1 уравнения 6 и неравенства 7 соответствует решение x1…xn неравенства 5.

Чтобы от зад сим формы перейти к зад канонич вида, необходимо ввести балансовые (выравнивающие) переменные. Это основано на теореме о неравенстве: любое нерав-во можно представить в виде ур-я или простейшего нерав-ва.

3. Геометрическая интерпретация целевой функции и ограничения злп. Геометрическая формулировка злп.

Пусть дана задача f=c1x1+c2x2-max (1)

a11x1+a12x2<=b1 }

am1x1+am2x2<=bm}

x1>=0, x2>=0 (3)

План задачи (х1,х2) – точка на плоскости. Каждое неравенство с-мы 2 предст. собой полуплоскость. Полуплоскость –выпуклое множество. Выпуклым наз-ся множество в которым точки отрезка соединяющие (х1 и х2) принадлежащие этому множеству то же принадлежат множеству. С-ма 2 представляет собой пересечение полуплоскостей. При пересечении могут получиться:

1)выпуклая многоугольная замкнутая область.

2) выпуклая открытая многоугольная область

3) единственная точка

4) пустое множество

5) луч и отрезок

Геометрическая интерпретация целевой функции: ф-ция 1 представляет собой семейство параллельных прямых, которые наз-ют линиями уровня(линиями постоянного значения целевой функции). Частные производные функции по х1 и х2 показывают скорость возрастания целевой функции вдоль координат осей. Вектор-градиент показывает направление найскорейшего возрастания целевой функции.Для задачи 1-3 вектор-градиент = (с1;с2) Выходит из точки (0,0) и направлен в точку с координатами (с1;с2). Вектор-градиент перпендикулярен линиям уровня. Пересечение полуплоскастей принято наз-ть областью допустимых рещений(ОДР).

4. Графический метод решения злп.

Графический способ целесообразно использовать для решения задач с двумя переменными, записанных в симметричной форме, а также для задач со многими переменными при условии, что в их канонической записи содержится на более двух свободных переменных. Порядок решения ЗЛП графическим способом:

1. Построить ОДЗ; 2. Построить вектор С; 3. Перпендикулярно С построить линию уровня f=0; 4. Перемещая линию уровня в градиентном направлении найти точку максимума или минимума ОДЗ; 5. Найти координаты точки максимума (минимума) и значение функции в этой точке. В ходе решения ЗЛП граф. способом могут получаться след. результаты:

1. Оптимальный план единственный: линия уровня и ОДЗ в крайнем положении имеют одну общую точку;

2. Оптимальных планов бесконечное множество: в разрешающем положении линия уровня проходит через грань ОДЗ;

3. Задача не имеет решения: ОДЗ=ø;

4. Целевая функция не ограничена, в этом случаи добавляется еще одно ограничение.

Граф.способом можно решать задачи с большим чем 2 количественных переменных. Если в канонической форме задачи разность м/у количеством линейно-независимых уравнений (r ) и количеством переменных n ровна 2. Для решения такой задачи: 1. преобразуют модель к симметрической форме, в результате получается задача ЗЛП с двумя независимыми; 2. решить ЗЛП граф.способом; 3. координаты точки экстремума подставить в уравнение канонич.записи и найти значение остальных переменных.