Федеральное агентство по образованию

ГОУ ВПО «Уральский государственный технический университет – УПИ»

ОПТИМАЛЬНЫЙ АЛГОРИТМ ПОИСКА НЕИСПРАВНОСТЕЙ

Методические указания к лабораторной работе по дисциплинам "Конструирование и технология РЭС", "Основы конструирования и технологии производства РЭС ", «Надежность, эргономика и качество АСОИУ», Надежность информационных систем» для студентов всех видов обучения специальностей:

2007 – Радиотехника; 2016 – Радиоэлектронные системы,

2205- Автоматизированные системы управления,

071900 - Информационные системы в технике и технологии

Екатеринбург, 2004

УДК 621.396.6.

Составители л.А. Чиркова

Научный редактор доцент, к.т.н. В.И. Иевлев

Оптимальный алгоритм поиска неисправностей

Методические указания к лабораторной работе по дисциплинам "Конструирование и технология РЭС", "Основы конструирования и технологии производства РЭС", «Надежность ИС», « Надежность, эргономика и качество АСОИУ»

Л.А. Чиркова Екатеринбург, изд-во УГТУ, 2004, 13 с.

В методических указаниях изложены теоретические основы оптимального поиска неисправности с использованием априорной информации о надёжности элементов системы. Исследуется триггер Шмидта по одиннадцати возможным отказам.

Практическая часть включает описание лабораторного стенда, домашнее задание, методику обработки экспериментальных данных, требования к отчету.

Библиогр.: 3 назв. Рис 2. Табл.6.

Подготовлено кафедрой «Технологии и средства связи»

В методических указаниях используются разработки доцента кафедры Г.С. Сергеева

Уральский государственный

Технический университет, 2004 г.

1. Цель работы

Целью данной лабораторной работы является:

• ознакомление студентов c алгоритмом оптимального поиска неисправностей;

• выработка у студента, как оператора системы «человек- машина», навыков оптимального обнаружения неисправностей с использованием априорных сведений о системе.

2. Продолжительность работы

Лабораторная работа выполняется в течении 4-часового занятия, включая 1 час на коллоквиум для оценки знаний студентов по теоретической части.

3. Теоретическая часть

3.1 Основы алгоритма оптимального поиска неисправностей

Отказы радиотехнических и автоматических систем приводят к вынужденным простоям. Время, потребное для восстановления, является величиной случайной, зависящей от характера отказов, квалификации обслуживающего персонала, от ремонтопригодности аппаратуры (приспособленности аппаратуры к обнаружению и устранению отказов). Известно, что 70-80% времени восстановления уходит на обнаружение отказавшего элемента, поэтому уменьшение времени обнаружения отказа является существенным резервом для повышения надёжности восстанавливаемых систем.

Пусть имеется объект контроля, состоящий из элементов, обладающих определенной надежностью. При выходе объ­екта из строя будем полагать, что причиной этого является неисправность одного из N элементов. События, заключающиеся в выходе из строя элементов, будем считать независи­мыми. Будем, далее, полагать, что при выходе объекта из строя вероятности того, что причиной этого события является j -й элемент, заданы и равны P_j. Очевидно, имеет место условие:

Обнаружение неисправности может быть произведено пу­тем проверки m параметров, характеризующих состояние объекта. Если параметр имеет значение в установленных пре­делах, будем обозначать этот исход проверки символом 1, если же параметр отклонился от допуска (безразлично, в какую сторону), то этот исход проверки будем обозначать символом 0. Будем считать, что значение параметра, определяемое ис­ходами проверки 1 или 0, известно в зависимости от со­стояния элемента (исправен он или неисправен). Эти данные можно получить либо специальным анализом влияния состояния объекта на измеряемые параметры, либо экспериментально, пу­тем искусственного введения неисправности в модель объек­та и измерения при этом контролируемых параметров. При неисправности k -го элемента некоторое количество контролируемых параметров примет значение 0, остальные будут иметь значение 1. Первоначально необходимо выбрать такое множество m параметров х_i, при котором не будет иметь место повторение комбинаций значений параметров при выходе из строя элементов. В результате предварительного анализа составляется таблица неисправностей (табл. 1), в которой записываются все контролируемые параметры х_i и исходы их проверок для всех возможных неисправностей n_j. В этой же таблице приводятся вероятности наличия той или иной неисправности P_j, которые рассчитываются в дальнейшем по формуле Байеса.

Таблица 1

Контролируе­мые параметры	Неисправности и их вероятности
	N1	n2	n3	N4	n5		nj		nN-1	nN
	P1	P2	P3	P4	P5	…	Pj	…	PN-1	PN
X1	0	0	0	0	0	…	0	…	-	0
X2	0	1	0	0	0	…	0	…	-	1
X3	0	0	0	0	1	…	0	…	1	1
X4	0	1	0	0	1	…	1	…	1	0
X5	1	0	0	0	0	…	0	…	0	1
…	.	.	.	.	.	…	.	…	.	.
Xj	.	.	.	.	.	…	.	…	.	.
…	.	.	.	.	.	…	.	…	.	.
…	.	.	.	.	.	…	.	…	.	.
Xm	0	0	1	1	1	…	1	…	1	1

Поскольку при проверке параметров возможны два исхода проверки (1 или 0), то наличие той или иной неисправности можно предсказать только с некоторой вероятностью. Вероят­ность появления значения 1 или 0 параметра х_i при вве­денных выше условиях есть вероятность появления хотя бы одной неисправности, отвечающей данному исходу проверки. Так, вероятность исхода проверки, при которой х_i примет значение 1, будет равна:

( 1)

где символ j1 обозначает суммирование только тех вероятностей P_j (табл.1), которые по параметру x_i дают значение 1. Очевидно, вероятноть исхода проверки, при которой x_i примет значение 0, равна:

(2)

Как видно из табл.1, для выявления любого из возможных неисправных элементов достаточно в определенной последовательности произвести проверку m параметров x_i, фиксируя каждый раз их значения. Наиболее просто произвести проверку последовательно от первого до m-го параметра. При этом для каждого неисправного элемента вся пос­ледовательность результатов проверки будет иметь вполне определенный вид. Например, последовательность 11110...1...1 соответствует, согласно табл.1 неисправности n_N-1.

Легко видеть, что табл.1 по существу является таблицей кода неисправных элементов объекта контроля, причем элементами кода будут параметра x_i с соответствующими значениями (0 или 1). Поскольку некоторые неисправные эле­менты могут быть однозначно определены неполным набором параметров x_i, число элементов в каждой кодовой группе может быть различным.

Пусть каждая проверка оценивается некоторым параметром _i. Это может быть время, затрачиваемое на провер­ку параметра x_i, стоимость проверки и т.д.

Тогда ''цена" L_j отыскания неисправного элемента j определится формулой:

где k_i – число параметров x_i, однозначно определяющих данную неисправность. Так, если время, затрачиваемое на каждую проверку, равно _i, то полное время обнаружения неисправности будет:

В дальнейшем, не внося существенных ограничений в общность результатов, будем полагать все _i одинаковыми. Тогда:

( 3)

где _x – время проверки любого из параметров x_i.

В начале параграфа мы отмечали, что в системах ав­томатического контроля отыскания неисправностей существенной характеристикой системы является скорость ее работы. Очевидно, если время проверки параметра фиксировано, то ско­рость отыскания неисправности будет тем выше, чем меньше параметров k_j будет проведено до момента обнаружения неисправности.

Т аким образом, критерием качества система автомати­ческого контроля целесообразно выбрать минимум среднего времени на отыскание неисправности. По существу, если об­ратиться к формуле (3), задача заключается в минимизации среднего числа проверяемых параметров на обнаружение одной неисправности. Введем понятие ''длительности" кодовой группы, определяющей данную неисправность как число элементов в ней. Так, последовательность результатов проверки, имеющая вид 1101101, является кодовой группой длительности в 7 двоичных единиц. Очевидно, длительности всех возможных кодовых групп будут находиться в пределах от 1 до m, так как возможны проверки, обнаруживающие неисправности как путем контроля только одного параметра, так и путем контроля всех m параметров. Эти длительности зависят от порядка контроля параметров, иными словами, одна и та же неисправность может быть закодирована различным образом. При этом общее число Q возможных кодовых групп, которыми можно закодировать неисправность, определяется числом контролируемых параметров m, комбинирующихся в различных сочетаниях от 1 до m:

(4)

Дальнейшая задача будет заключаться в том, чтобы построить код неисправностей, обладающий минимальной сред­ней длительностью кодовых групп. Другими словами, надлежит найти такую последовательность проверок параметров, которая позволила бы обнаружить неисправный элемент объекта контроля при минимальном числе проверок.

Каждая проверка доставляет определенную информацию о сос­тоянии объекта и, таким образом, уменьшает энтропию рас­сматриваемой ситуации. Отсюда следует, что длительность кодовой группы кода неисправностей будет определяться значениями прироста информации при каждой проверке. Чем значительнее этот прирост, тем короче будет кодовая группа, а следовательно, и меньше число проверок.

При проверке параметра x_i неопределенность исхода проверки определяется энтропией:

( 5)

где вероятности P_i0 и P_i1 определяются формулами (1) и (2). Максимальное значение энтропии H(x_i) будет при равенстве вероятностей P_i0 и P_i1, следовательно, для получения максимальной информации на первом шаге проверку надо начинать с того параметра, у которого вероятности P_i0 и P_i1 наиболее близки.

Способ построения оптимального алгоритма проверок опирается на формулу (5).

Как было отмечено выше, сокращение числа шагов при проверке (т.е. сокращение длительности кода неисправностей) может быть достигнуто путем извлечения максимальной информации о состояний объекта при каждом шаге проверки. Это означает, что необходимо каждый раз проверять тот из параметров, который изменяет максимальную энтропию H(x_i) при данном опыте, что отвечает минимальной разности вероятностей P_i0 и P_i1. Первый шаг заключается в составлении таблицы вероятностей P_i0 и P_i1 и их разностей для всех параметров по формулам (1) и (2) (см. табл. 2).

Таблица 2

Вероятности	Параметры
	X1	X2	X3	…	Xm
Pi0	P10	P20	P30	…	Pm0
Pi1	P11	P21	P31	…	Pm1
Pi	P1	P2	P3	…	Pm

Параметр, имеющий минимальное значение P_i выбирается первым для проверки. Пусть, например, это будет параметр Х₄ табл.1. Так как этот параметр может при проверке дать значение либо 1, либо 0, дальнейшая цепочка проверок разветвляется. Приняв значение первого проверяемого параметра (для нашего примера Х₄) равным 1, находим суммы вероятностей для исходов 1 и 0. При этом суммируются вероятности только тех колонок табл.1, которые соответствуют исходам 1 первого проверяемого параметра (Х₄). Приняв затем значение первого проверяемого параметра (Х₄) равным 0, проделываем аналогичную процедуру. Табл. 3 иллюстрирует описанную операцию для примера табл. 1.

Таблица 3

Параметры	Их исходы	X4=1	X4=0
X1	1 0	P1+P5+PN-1 P2+Pj	P3+P4 PN
X2	1 0	P1+P2+PN-1 P5+Pj	P3+PN P4
X3	1 0	P5+PN-1 P1+P2+Pj	PN P3+P4
…..	…	………………	……………….

Обозначим найденные суммарные вероятности P_i1(X₄=1), P_i0(X₄=1), P_i1(X₄=0) и P_i0(X₄=0), где индекс i указывает, к какому параметру относится значение вероятности.

Так, например, в соответствии с табл. 3

P₁₁(X₄=1) = P₁+P₅+P_N-1, P₂₀ = P₅+P_j, P₃₁(X₄=0) = P_N

и т.д. По полученным значениям вероятностей определяются их разности P_i(X₄=1) и P_i(X₄=0) для всех оставшихся параметров и из каждой группы выбирается минимальная разность. Тем самым будут определены два параметра, наиболее выгодные для последующего контроля системы. Пусть это будут, для примера, параметры X₁ и X₃ поскольку P₁(X₄=1) = min и P₃(X₄=0) = min. Но параметры X₁ и X₃ в свою очередь при проверке могут дать значение либо 1, либо 0. Таким образом, каждая из наметившихся двух цепочек проверок разветвляется. На рис.1 показана примерная схема построения оптимального алгоритма.

X₄ P₄=min

1 0

P₁₁ (X₄=1) = min X₁ X₃ P₃₀ (X₄=1) = min

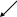
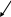
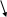
1 0 1 0

P₂₁ (X₄=1;X₁=1)=X₂ X₂ X₅ X₇ X₆ P₆₀ (X₄=0;X₃=0) = min

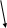
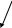
1 0 и т.д. 1 0

I IV II

Рис. 1

Рассмотрение дальнейших шагов по построению цепочек проверок удобнее всего произвести по этой схеме.

Аналогично предыдущему по таблице неисправностей (типа табл. 1) при значениях (X₄=1; X₁=1) и (X₄=1; X₁=0) определяются суммарные вероятности неисправностей P_ij (X₄=1; X₁=1), P_i1(X₄=1; X₁=0)=min для каждого из оставшихся параметров, находятся их разности и пo минимальным разностям P_i (X₄=1; X₁=1)=min; P_i (X₄=1; X₁=0)=min определяются следующие параметры для контроля, пусть это будут X₂ и X₅ соответственно.

Аналогичные операции с параметром Х₃ дадут P_i (X₄=0; X₃=1)=min; P_i (X₄=0; X₃=0)=min этим минимальным разностям будут соответствовать параметры X₆ и X₇.

Построение цепочек по рассмотренной методике продолжается до тех пор, пока не будет получено однозначное соответствие между проверкой и неисправностью. Алгоритм проверок при этом будет обеспечивать минимальное в среднем число шагов для обнаружения любого из возможных неисправных элементов контролируемого объекта.

Рассмотренная методика построения оптимального алгоритма поиска неисправностей, опирающаяся на информационные представления, легко может быть распространена и на другие аналогичные задачи. Так, вполне осуществимо построение алгоритма поиска для случая, когда контролируемые параметры имеют не два, а больше возможных состояний, однако при этом вычисления существенно усложняются и требуется привлечение вычислительных машин.