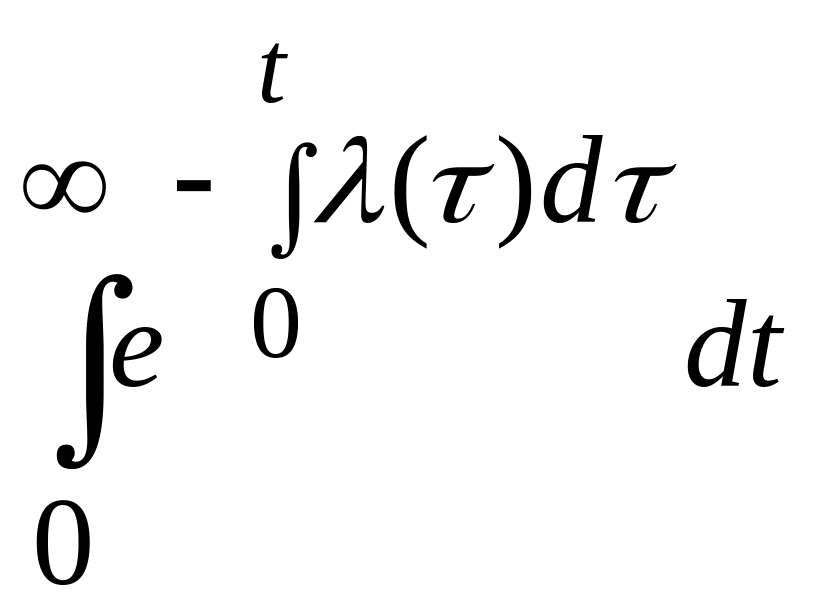- •1. Основные понятия, термины и определения 8
- •2. Количественные показатели аппаратурной надежности асоиу 27
- •3. Математические модели надежности аппаратуры асоиу 41
- •4. Расчет надежности невосстанавливаемой аппаратуры асоиу на этапе проектирования 49
- •5. Расчет надежности ремонтируемых систем 63
- •6. Основы моделирования и расчета надежности программных средств 73
- •7. Основы эргономики асоиу 87
- •8. Основы организации испытаний асоиу на надежность 107
- •9. Основные принципы обеспечения качества промышленной продукции 117
- •Введение
- •1. Основные понятия, термины и определения
- •1.1. Система и ее элементы
- •1.2. Основные функции асоиу
- •1.3. Понятия надежности и отказа системы (элемента)
- •1.4. Основные определения в области качества и надежности программного обеспечения (по) асоиу
- •1.5. Основные определения в области надежности подсистемы человек-оператор асоиу
- •1.6. Факторы, влияющие на надежность асоиу
- •1.6.1. Контроль технического состояния асоиу в процессе эксплуатации
- •1.6.2. Влияние внешних воздействующих факторов при эксплуатации асоиу
- •1.7. Проблема стандартизации в области надежности и качества
- •2. Количественные показатели аппаратурной надежности асоиу
- •2.1. Основные показатели надежности невосстанавливаемых объектов
- •2.1.1. Вероятность безотказной работы
- •2.1.2. Вероятность отказа
- •2.1.3. Средняя наработка до отказа
- •2.1.4. Интенсивность отказов
- •2.2. Показатели надежности восстанавливаемых объектов
- •2.2.1. Показатели безотказности восстанавливаемых объектов
- •2.2.1.1. Параметр потока отказов
- •2.2.1.2. Средняя наработка на отказ объекта
- •2.2.2. Показатели ремонтопригодности
- •2.2.2.1. Вероятность восстановления
- •2.2.2.2. Среднее время восстановления
- •2.2.2.3. Интенсивность восстановления
- •2.2.3. Показатели долговечности
- •Комплексные показатели надежности
- •2.3.1. Коэффициент готовности
- •2.3.2. Коэффициент оперативной готовности
- •2.3.3. Коэффициент технического использования
- •Коэффициент сохранения эффективности
- •3. Математические модели надежности аппаратуры асоиу
- •3.1. Модели потоков событий
- •3.1.1. Простейший поток отказов
- •3.1.2. Потоки Эрланга
- •3.2. Законы распределения дискретных случайных величин
- •3.2.1. Биномиальный закон распределения числа появления события а в m независимых испытаниях
- •3.2.2. Пуассоновское распределение появления n событий за время t
- •3.3. Законы распределения непрерывных случайных величин
- •3.3.1. Экспоненциальное распределение
- •3.3.2. Нормальное распределение
- •3.3.3. Гамма-распределение
- •3.4. Модели случайных процессов
- •3.3.1. Марковские процессы
- •4. Расчет надежности невосстанавливаемой аппаратуры асоиу на этапе проектирования
- •4.1. Составление логических схем
- •4.2. Расчет надежности нерезервированной невосстанавливаемой системы
- •Учет влияния режимов работы элементов на надежность
- •4.4. Расчет надежности невосстанавливаемых резервированных систем
- •4.4.1. Резервирование с целой кратностью с постоянно включенным резервом или нагруженное резервирование замещением с абсолютно надежными переключателями
- •4.4.1.1. Общее резервирование
- •4.4.1.2. Раздельное резервирование
- •4.4.1.3. Общее резервирование с дробной кратностью
- •4.4.2. Резервирование замещением ненагруженное и облегченное с абсолютно надёжными переключателями
- •4.4.2.1.Общее ненагруженное резервирование замещением
- •4.4.2.2. Облегченное резервирование замещением
- •В случае показательного распределения наработки до отказа
- •4.4.3. Резервирование с учетом надежности переключателей
- •4.4.4. Скользящее резервирование
- •5. Расчет надежности ремонтируемых систем
- •5.1. Общая характеристика методов расчета надежности ремонтируемых систем
- •Вычисление функций готовности и простоя нерезервированных систем
- •5.3. Особенности расчета резервированных систем
- •5.3.1. Ненагруженное резервирование с восстановлением
- •5.3.2. Нагруженное резервирование замещением
- •Расчет надежности восстанавливаемых систем, перерывы в работе которых в процессе эксплуатации недопустимы
- •Примеры решения типовых задач
- •Основы моделирования и расчета надежности программных средств
- •6.1. Модель анализа надежности программных средств
- •6.2. Статистика ошибок по асоиу
- •6.3. Количественные характеристики надежности по асоиу
- •6.4. Модели надежности программного обеспечения
- •6.4.1. О возможности построения априорных мнп
- •6.4.2. Непрерывные эмпирические модели надежности по (нэмп)
- •6.4.3. Дискретные эмпирические модели надежности по (дэмп)
- •6.5. Способы обеспечения и повышения надежности по
- •6.5.1. Основы организации тестирования программ
- •6.5.1.1. Особенности тестирования « белого ящика»
- •6.5.1.2. Особенности функционального тестирования по ( методы тестирования «черного ящика»)
- •6.5.1.3. Организация процесса тестирования программного обеспечения
- •6.5.2. Способы оперативного повышения надежности по
- •Основы эргономики асоиу
- •7.1. Основные понятия и определения
- •7.2. Классификация эргономических методов исследования
- •7.3. Характеристика деятельности человека-оператора технических систем
- •7.4. Влияние человека - оператора на надежность асоиу
- •Показатели безошибочности человека-оператора
- •7.4.2. Способы борьбы с ошибками оператора
- •7.5. Проектирование дружественных пользователю вычислительных систем
- •7.5.1. Эргономика средств ввода информации
- •7.5.2. Работа с дисплеями и требования к ним
- •7.5.3. Организация компьютеризованных рабочих мест
- •7.6. Организация диалога человека и эвм
- •8. Основы организации испытаний асоиу на надежность
- •8.1. Виды испытаний на надежность
- •Принципиальные особенности организации испытаний на надежность асоиу
- •Основы организации определительных испытаний на надежность
- •8.3.1. Точечные оценки показателей безотказности и ремонтопригодности
- •8.3.2. Оценка показателей надежности доверительным интервалом
- •8.3.2.1. Определение доверительного интервала для средней наработки на отказ
- •8.3.2.2. Определение доверительного интервала для вероятности безотказной работы по числу обнаруженных при испытаниях отказов
- •8.4. Основы организации контрольных испытаний
- •9. Основные принципы обеспечения качества промышленной продукции
- •9.1. Современная концепция обеспечения качества продукции
- •Наименование детали
- •Два подхода к контролю за качеством продукции
- •Заключение
2.1.4. Интенсивность отказов
На
практике достаточно часто приходится
определять
![]() - вероятность
безотказной работы объекта в заданном
интервале времени [t1,
t2]
, где t1
<
t2
.
- вероятность
безотказной работы объекта в заданном
интервале времени [t1,
t2]
, где t1
<
t2
.
Эта вероятность является условной, поскольку безотказная работа объекта на отрезке времени [t1, t2] возможна только при условии, что на отрезке времени [0, t1] объект был работоспособен.
Вероятность
![]() -
вероятность
безотказной работы объекта на отрезке
времени [0, t2]
- является вероятностью совместного
появления двух зависимых событий:
безотказной работы объекта на отрезке
времени [0, t1]
и безотказной работы объекта на отрезке
времени [t1,
t2].
-
вероятность
безотказной работы объекта на отрезке
времени [0, t2]
- является вероятностью совместного
появления двух зависимых событий:
безотказной работы объекта на отрезке
времени [0, t1]
и безотказной работы объекта на отрезке
времени [t1,
t2].
На основании формулы полной вероятности [2.1] запишем
![]() ,
откуда
,
откуда
![]() .
(2.10)
.
(2.10)
Определим теперь вероятность отказа объекта - Q (t1, t2) на отрезке времени [t1, t2] при условии, что на отрезке времени [0, t1] объект был работоспособен.
Согласно
(2.4), (2.10)
![]() .
.
Допустим
теперь, что
![]() где
где
![]() .
.
Тогда
![]() .
.
Поделим
и умножим полученное выражение на
![]() .
.
![]() .
.
Величина,
равная
![]() ,
называется интенсивностью
,
называется интенсивностью
отказов
-
![]() .
.
Интенсивность отказов - это условная плотность вероятности возникновения отказа объекта на бесконечно малом интервале времени [t, Δt], определяемая при условии, что до рассматриваемого момента времени t отказ не наступил.
Из определения следует, что
![]() .
(2.11)
.
(2.11)
Интегрируя правую и левую часть выражения (2.11), а затем, избавляясь от логарифма в правой части, получим:
![]() или
или
![]() .
(2.12)
.
(2.12)
Выражение (2.12) показывает связь λ (t) и P(t): вероятность безотказной работы убывает экспоненциально в соответствие с интенсивностью отказов. По аналитически заданной функции λ (t) можно определить не только P(t), но и Т1:
 .
(2.13)
.
(2.13)
Статистическая оценка интенсивности отказов имеет вид:
 ,
(2.14)
,
(2.14)
где
![]() -
число отказов однотипных объектов на
интервале
-
число отказов однотипных объектов на
интервале ![]() ,
для которого определяется
,
для которого определяется ![]() ;
;
![]() -
число работоспособных объектов в
середине интервала
.
-
число работоспособных объектов в
середине интервала
.
![]() ,
,
где Ni - число работоспособных объектов в начале интервала ; Ni+1- число работоспособных объектов в конце интервала .
Если
интервал
уменьшается
до нулевого значения
![]() ,
то
,
то
![]() ,
(2.15)
,
(2.15)
где Nо - количество объектов, поставленных на испытания;
∆ti - интервал, продолжающий время t;
n( ) - количество отказов на интервале .
Если для статистической оценки интенсивности отказов - λ (t) время эксперимента разбить на достаточно большое количество одинаковых интервалов Δt и провести наблюдения в течение длительного периода времени t , то результатом обработки опытных данных будет график, изображенный на рис. 2.2.
Как показывают многочисленные экспериментальные данные по анализу надежности технических объектов, в том числе и ЭВМ, линеаризованная обобщенная зависимость λ(t) представляет собой сложную кривую с тремя характерными интервалами (I, II, III). На интервале II (t2 – t1) λ(t) = const. Это - период нормальной эксплуатации объектов. Для электронных компонентов он может составлять десятки лет [2.1, 2.2, 2.3].
Интервал I (0, t1) часто называют периодом приработки объектов. Он может увеличиваться или уменьшаться в зависимости от уровня организации производства на заводе-изготовителе, где элементы с внутренними дефектами своевременно изымаются из партии выпускаемой продукции. Величина интенсивности отказов на этом интервале во многом зависит от качества сборки схем сложных устройств, соблюдения требований монтажа и т.п. Включение под нагрузку собранных схем приводит к быстрому "выжиганию" дефектных элементов и по истечении некоторого времени t1 в схеме остаются только исправные элементы, и их эксплуатация связана с λ (t) = const.

Рис. 2.2. Линеаризированная усредненная кривая жизни элемента:
I – интервал приработки; II – интервал нормальной эксплуатации; III – интервал старения
На интервале III (t > t2) по причинам, обусловленным естественными процессами старения, изнашивания и т.д., интенсивность отказов резко возрастает, увеличивается число деградационных отказов.
Для того чтобы обеспечить λ(t) = const, необходимо заменить неремонтируемые элементы на исправные новые или работоспособные, отработавшие время t << t2. Работа устройства на интервале времени, для которого λ(t) = const, может быть описана экспоненциальным законом распределения вероятности безотказной работы. Эта модель подробно проанализирована в подразделе 3.3. Здесь же отметим, что при λ(t) = const значительно упрощается расчет надежности, поэтому интенсивность отказов λ(t) наиболее часто используется как исходный показатель надежности элементной базы [2.1, 2.2, 2.3]. В заключение этого параграфа приведем сводную таблицу связи показателей безотказности невосстанавливаемых объектов ( табл. 2.1)
Таблица. 2.1
Связь между показателями безотказности
Базовые параметры |
P(t) |
Q(t) |
f(t) |
λ(t) |
T1 |
P(t)
|
|
|
|
|
|
Q(t) |
1-Q (t) |
|
|
|
|
f(t) |
|
|
|
|
|
λ(t) |
|
|
|
|
|