6.3. Решение уравнений движения машины

Система дифференциальных уравнений движения содержит две неизвестные функции времени закон движения входного звена исполнительного механизма q(t) и движущий момент Q(t). Для отыскания стационарного решения этих уравнений обычно пользуются методом последовательных приближений. В данной курсовой работе используется ранее полученное решение.

1. Внутренняя виброактивность. Нахождение возмущающего момента.

Возмущающий момент – характеризует возмущение, вызывающее отклонение закона движения входного звена (кривошипа) от программного (равномерного) вращения, также характеризует внутреннюю виброактивность исполнительного механизма:

,

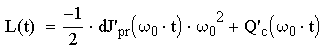где:

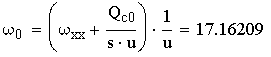
Далее производится разложение возмущающего момента на программном движении q = ω₀ в ряд Фурье с точностью до пяти гармоник:

,

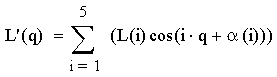где:

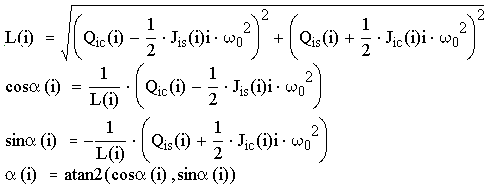
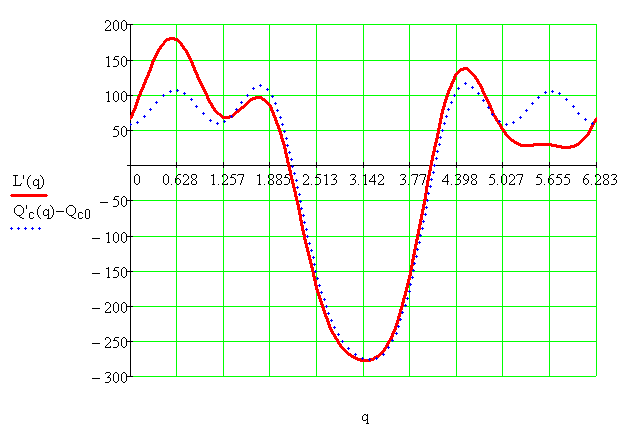
Рис. 6.5. Совмещённый график возмущающего момента и переменной части приведенного момента сил сопротивления, разложенного в ряд Фурье

2. Далее ищется динамическая ошибка по углу с точностью до пяти гармоник:

,

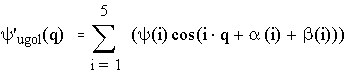где:

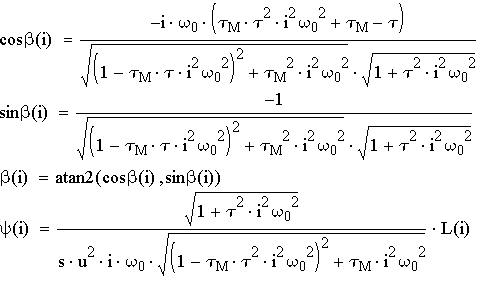
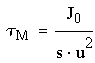- механичская постоянная времени машины.

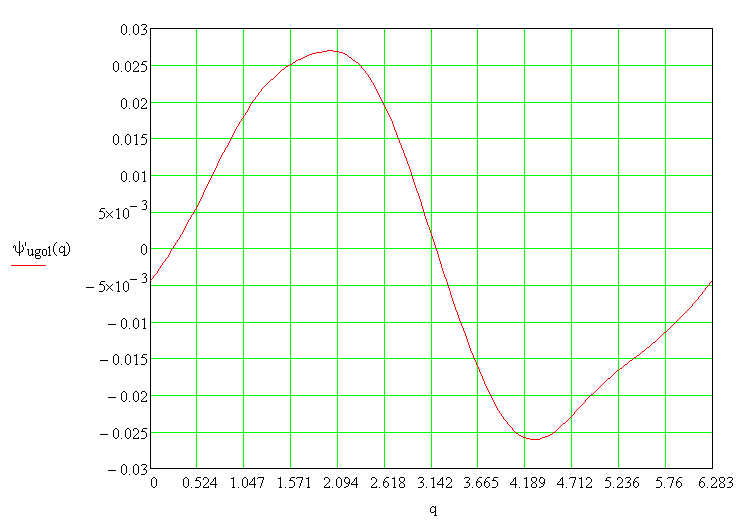
Рис. 6.6. Динамическая ошибка по углу

3. Нахождение динамической ошибки по скорости:

,

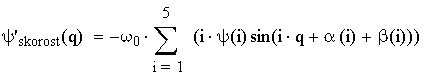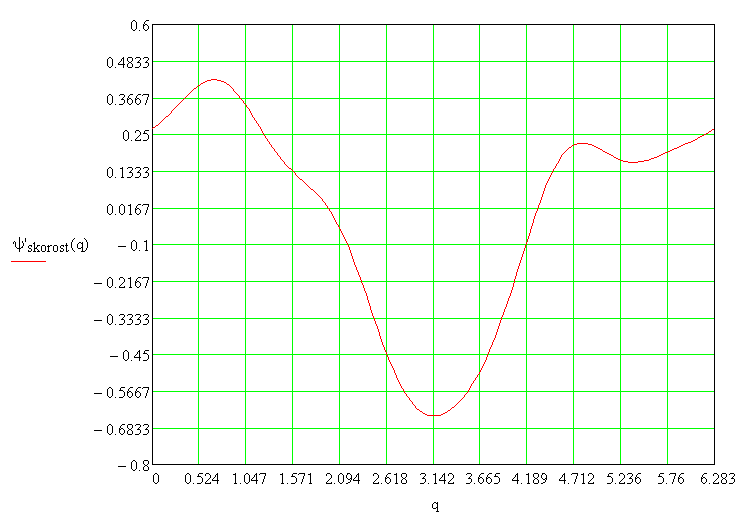
Рис.6.7. Динамическая ошибка по скорости

4. В технических требованиях к машине часто задаются допустимые значения максимальных динамических ошибок, оцениваемые коэффициентами неравномерности вращения входного звена:

,

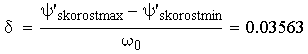где:

Рассчитанный коэффициент неравномерности вращения входного звена не превышает допустимого значения 0,04.

5. Далее находится переменная часть движущего момента с точностью до пяти гармоник:

,

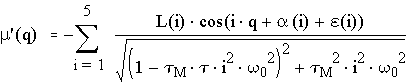где:

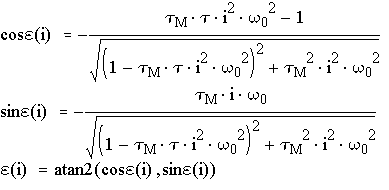
Тогда закон изменения движущего момента при учете механической

характеристики двигателя с точностью до пяти гармоник определяется по формуле:

,

где:

График движущего момента, полученного в динамическом исследовании представлен на Рис. 6.8.

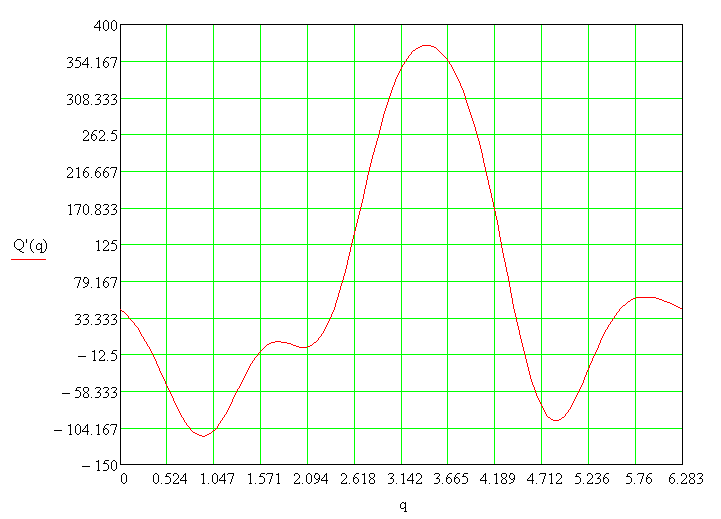
Рис. 6.8. График движущего момента, полученного при динамическом исследовании

6.4. Построение динамических нагрузок машины

Важной динамической характеристикой установившегося движения являются динамические нагрузки в передаточном механизма. Их можно определить из уравнения вращательного движения ротора двигателя.

Крутящий момент в приводе определяется с точностью до пяти гармоник:

,

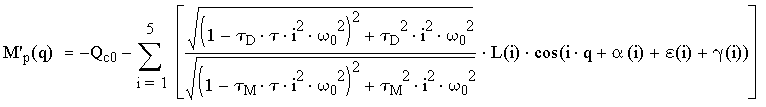где:

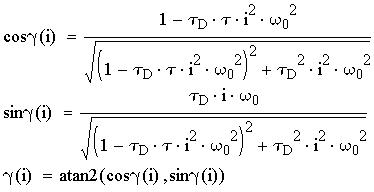
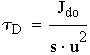- механическая постоянная привода;

- момент инерции ротора двигателя и передаточного механизма, приведенный к входному звену.

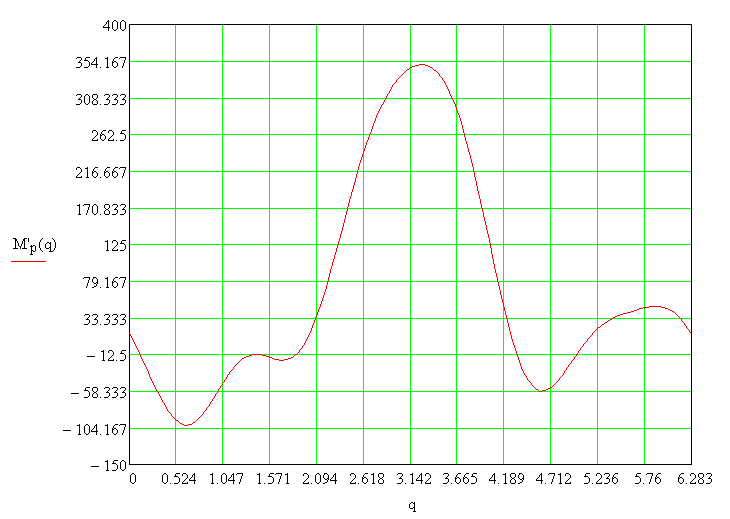
Рис. 6.9. Крутящий момент в приводе

6.5. Улучшение показателей качества машины

Основное требование конструирования: знакопостоянство крутящего момента, обеспечивающее отсутствие перекладки зазоров в зубчатых передачах редуктора. Этот момент, который действует на редуктор и приведен к выходному валу редуктора. Нарушение данного условия ведет к увеличению ударной нагрузки на зубья и быстрому износу передачи.

В машине, рассматриваемой в курсовом проекте, произошла перекладка зазоров. Существует несколько способов обеспечения знакопостоянства крутящего момента:

• Увеличение среднего значения приведённого момента инерции, что обеспечивается установкой маховика;

• Увеличение среднего значения приведённого момента сил сопротивления, что достигается установкой тормозного устройства;

• Установка динамического гасителя или разгружателя, и т.д.

В данном случае был выбран наиболее рациональный метод – увеличение среднего значения приведённого момента инерции путём установки маховика.

Осевой момент инерции маховика был подобран эмпирическим путём:

Вычисление параметров маховика:

- радиус маховика;

-диаметр маховика;

- масса маховика.

Другим показателм качества машины является характер разбега.

Разбег с учётом динамической характеристики двигателя описывается частным решением уравнения:

,

соответствующим определённым начальным условиям:

1. 

2. 

Сначала составляется характеристичекое уравнение:

Корни характеристическогоуравнения:

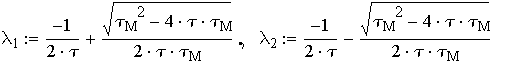
Рассматриваемый механизм будет иметь разбег ввиде затухаюзщего колебательного процесса, поскольку:

В этом случае угловая скорость будет изменяться по следующему закону:

,

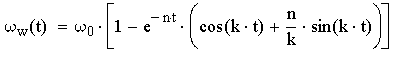где:

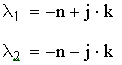
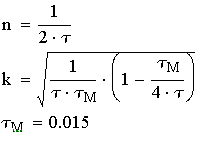
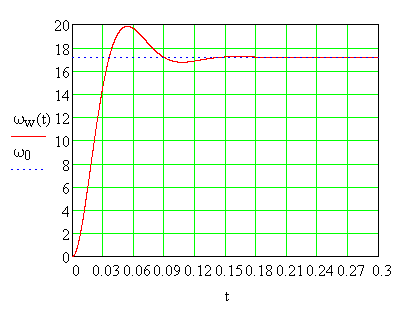
Рис. 6.10. Изменение угловой скорости за время разбега при колебательном процессе

Время разбега t_р=0,18с.

Однако следует стремиться к тому, чтобы разбег был апереодическим процессом. Для этого можно поставить дополнительный маховик, тем самым увеличив механическую постоянную времени.

Параметры подобранного маховика:

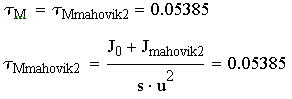
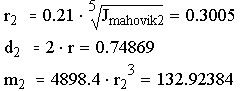
Функция угловой скорости в этом случае имеет вид:

,

где:

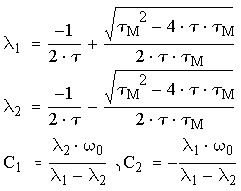
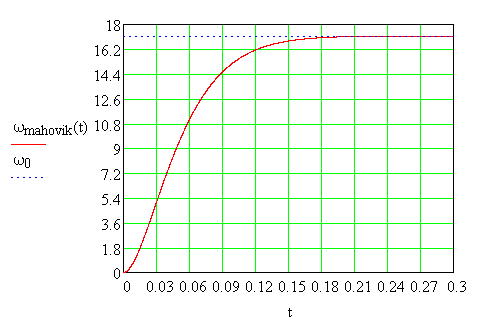
Рис. 6.11. Изменение угловой скорости за время разбега при апериодическом процессе

При этом время разбега увеличивается t_p=0,21с, но это значение невелико, поэтому является пиемлемым.