5.9. Оценка внешней виброактивности исполнительного механизма

Свойство механизма во время движения воздействовать на корпус машины переменными силами называется внешней виброактивностью. Мерой внешней виброактивности механизма являютя усилия, действующие на корпус машины, численно равные главным векторам и главным моментам внешних активных сил и сил инерции.

В большинстве случаев ативные силы, приложенные к звеньям механизма, оказываются по отношению к машине в целом внутренними.

В плоском механизме ограничиваются определением главного вектора и главного момента внешних реакций, лежащих в плоскости движения.

5.10. Уравновешивание сил инерции

На этом этапе выполняется уравновешивание главного вектра сил инерции рычажного механизма. Для этого определяются проекции главного верктора путём суммирования соответствующих проекций отдельных звеньев:

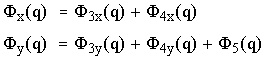
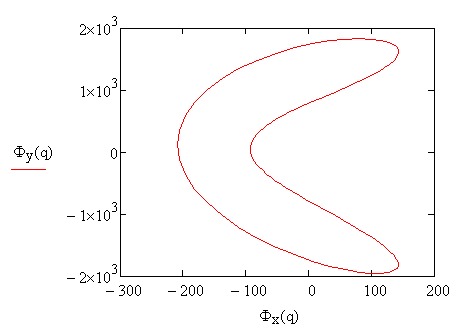
Рис.5.9. Гадограф главного вектора сил инерци

Смысл уравновешивания механизма на основе гармонического анализа заключается в том, что эллиптическую гармонику разлагают на две круговые гармоники, а затем каждую из круговых гармоник уравновешивают с помощью противовесов, установленных на кривошипе и на зубчатых колесах.

Расчёт представлен для первых гормоник, для остальных четырёх расчёт выполнялся аналогично.

Для этого определяют массы противовесов:

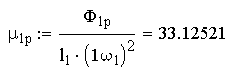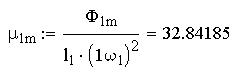, кг

, кг,

где:

Ф._1p, Ф._1m – модули круговых гормоник.

,

где:

a._1p, b._1p, a._1m, b._1m – коэффициенты круговых гормоник.

,

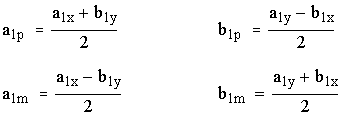где:

- коэффициенты ряда Фурье (эллиптических гормоник).

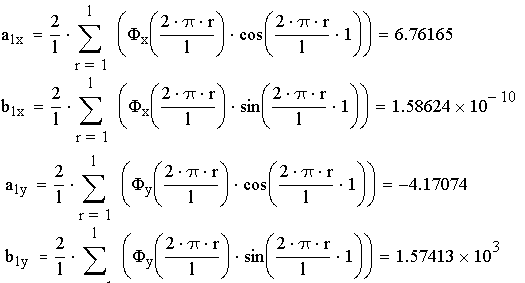
Также определяются углы установки противовесов:

,

где:

θ._1p, θ._1m - начальные углы круговых гармоник.

,

где:

Таким образом находятся усилия, передаваемые на корпус машины после установки противовесов:

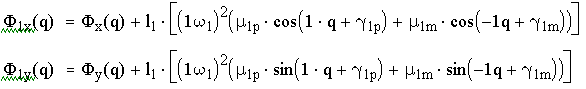
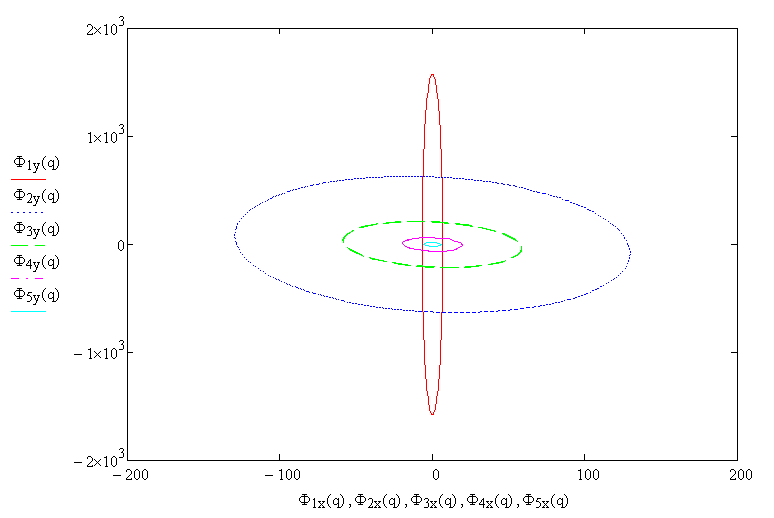
Рис.5.10. График пяти эллептических гормоник

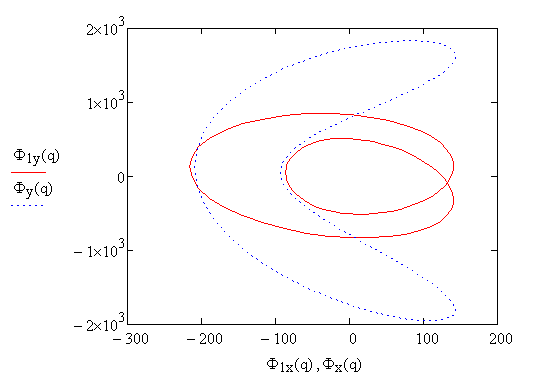
Рис.5.11. Годограф главного вектора сил инерции до уравновешивания и после

5.11. Выводы

В результате силового расчета были определены реакции в кинематических парах, оценена достоверность результатов расчета. Расхождения в решениях, найденных различными методами, не превышают 0.01 %. Был рассчитан движущий момент и по нему выбран двигатель, подобрана схема редуктора. Кроме того, была оценена внешняя виброактивность и принято решение о целесообразности установки противовесов, по изменению главного вектора сил инерции и массе механизма.

6. Динамическое исследование машинного агрегата

6.1. Задачи динамического анализамашины

Задачей динамического исследования машины является определение закона движения входного звена исполнительного механизма q(t) с учетом динамических свойств приводного двигателя, движущего момента Q(t) и динамической нагрузки в приводе M_п(t), а также оценка неравномерности вращения входного звена и проверка перекладки зазоров в приводе, улучшение динамических показателей качества машины.

6.2. Построение динамической и математической модели машины

Машинный агрегат состоит из двигателя, передаточного и исполнительного механизмов.

Динамический расчет машинного агрегата связано с определением и исследованием стационарного решения системы дифференциальных уравнений:

где:

q – обобщённая координата, угол поворота входного звена;

J_пр(q) – приведённый момент инерции механической системы;

Q – обобщённая движущая сила, силовая характеристика;

Q_c – приведённый момент сил сопротивления;

Q_cm( )– приведённая статическая характеристика двигателя, разрешённая относительно момента

τ – постоянная времени двигателя

Второе уравнение является приведённой динамической характеристикой двигателя.

Сначала определяются коэффициенты, входящие в систему дифференциальных уравнений.

1. Приведенный момент инерции определяется как коэффициент при половине квадрата обобщённой скорости в выражении кинетического энергии механической системы.

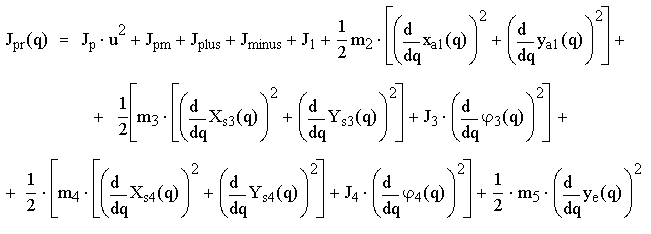
где:

J_p – момент инерции ротора двигателя;

u – передаточное число редуктора;

– приведённый момент инерции редуктора;

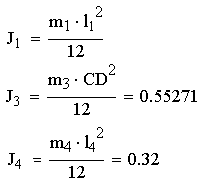
- осевые моменты инерции звеньев 1, 4, CD;

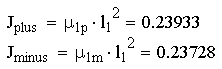
- моменты инерции противовесов;

Полученная функция J_pr(q) с целью упрощения динамических расчетов раскладывается в ряд Фурье с точностью до пяти гармоник:

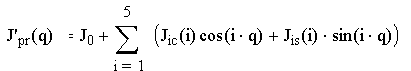
где:

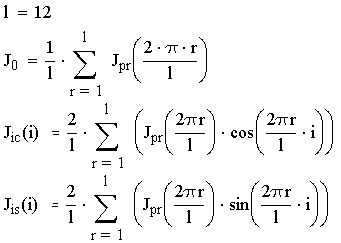
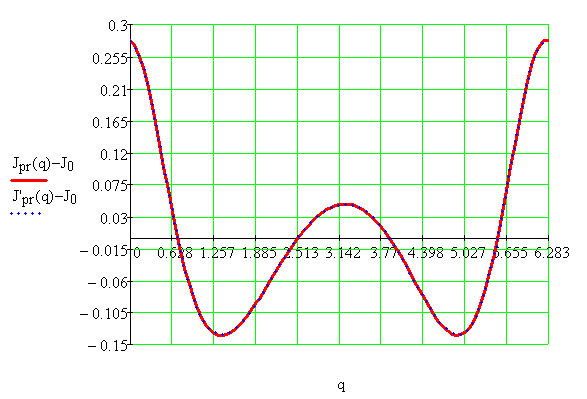
Рис. 6.1. Разложенный в ряд Фурье приведённый момент инерции

2. Вычисление производной от момента инерции по обобщённой координате:

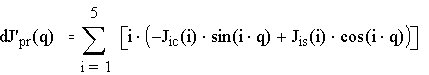
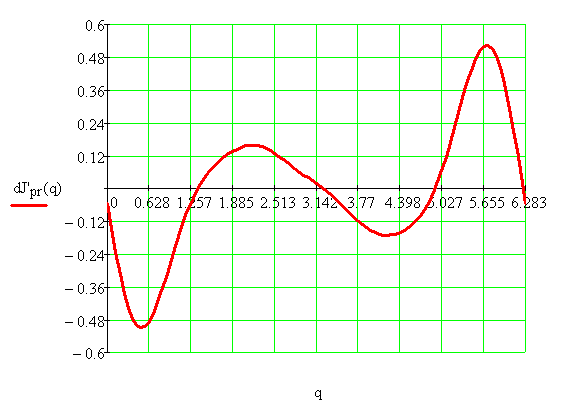
Рис. 6.2. Производная от приведённого момента инерции по обобщённой координате

3. Приведенный момент сил сопротивления определяется как коэффициент при вариации обобщённой координаты в выражении для возможной работы активных сил сопротивления (рабочей нагрузки и сил тяжести):

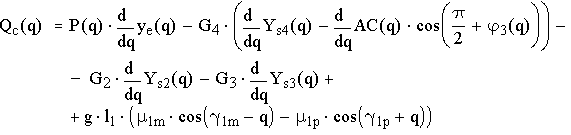
Функция Q_c(q) раскладывается в ряд Фурье с точностью до пяти гармоник:

где:

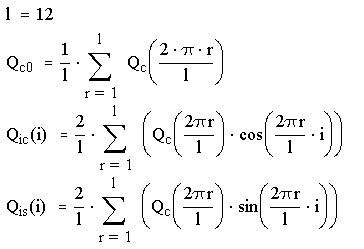
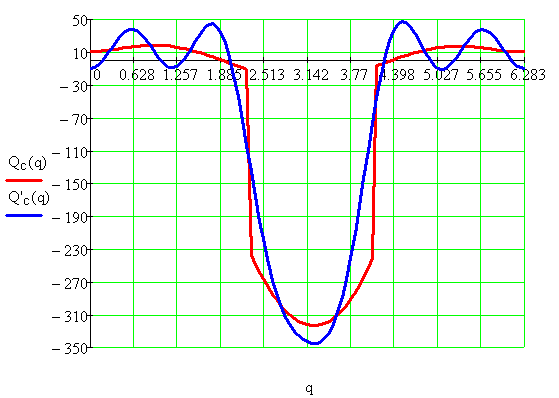
Рис. 6.3. Разложенный в ряд приведенный момент сил сопротивления и приведенный момент сил сопротивления

4. Уравнение статической характеристики электродвигателя постоянного тока независимого возбуждения:

,

где:

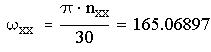
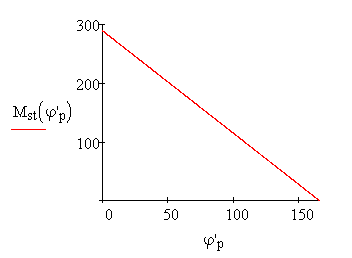
Рис. 6.4. Статическая характеристика двигателя

Приведённая статическая характеристика двигателя определяется как обобщённая сила: