Структурный анализ механизма прототипа №2
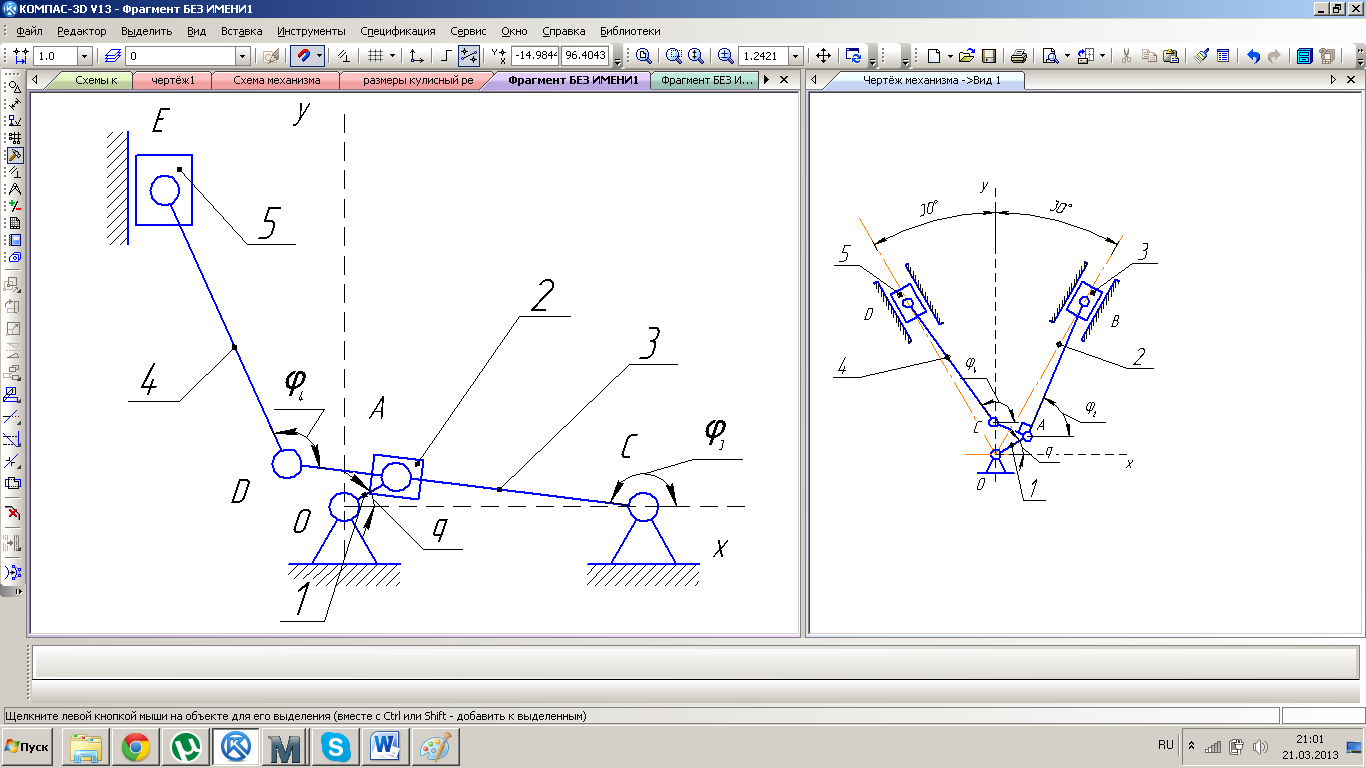
Рис.2.4. Структурная схема прототипа №2
Механизм состоит из шести звеньев:
0 – стойка и направляющие – неподвижное звено;
1 – кривошип, совершающий вращение вокруг неподвижной оси;
2 – камень кулисы, совершающий возвратно-поступательное движение по кулисе;
3 – кулиса, совершающая качательное движение;
4 – шатун, совершающий плоское движение;
5 – ползун, совершающий возвратно-поступательное движение.
Количество подвижных звеньев N = 5.
Количество входов n = 1.
Число степеней подвижности Wп определено по формуле Чебышёва (3.1):
где: N=5, pН=7, рВ=0.
Рассматриваемый механизм нормальный, поскольку число входов совпадает с числом степеней подвижности (Wп=n), что позволяет провести геометрический анализ.
Граф механизма, выявление структурных групп и граф структуры.
Рис.2.5. Граф механизма
Рис.2.6. Граф структуры
Выявлено 3 структурные группы:
0-1 – однозвенная одноподвижная группа;
2-3 – ВПВ, двухзвенная 0-подвижная группа;
4-5 – ВВП, двухзвенная 0-подвижная группа.
Геометрический анализ механизмов
Задачи геометрического анализа механизмов
Задачами геометрического анализа механизма являются: построение функции положения выходных звеньев, исследование функции положения и построение графиков.
Составление и решение уравнений геометрического анализа
Прототип №1.
Групповые уравнения для группы ВВВ:
Необходимые уравнения для определения функции положения 1-й группы:
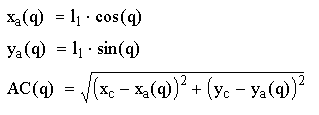(3.2)
М = -1
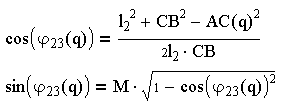
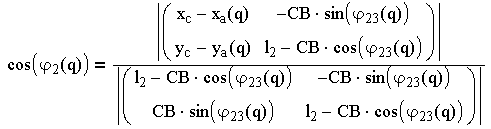
Решением системы уравнений в общем виде определяются функции положения:
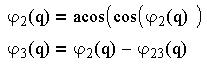(3.3)
Групповые уравнения для группы ВВП:
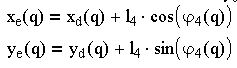(3.4)
Необходимые уравнения для определения функции положения 2-й группы:
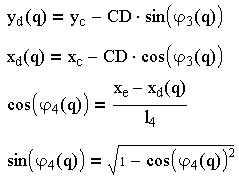(3.5)
Решением системы уравнений в общем виде определяются функции положения:
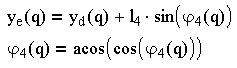(3.6)
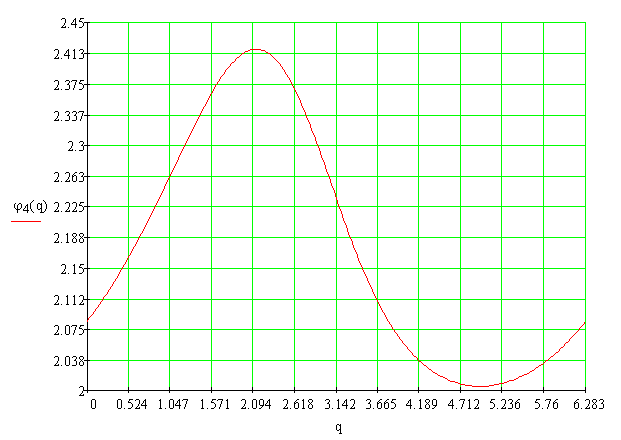
Рис.3.1. График функции положения φ4
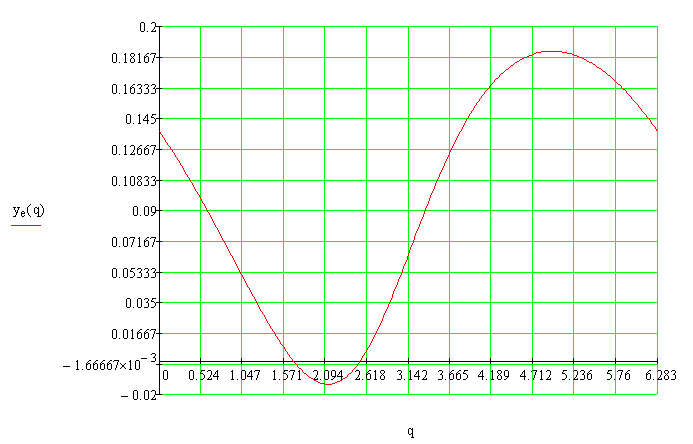
Рис.3.2. График функции положения yе
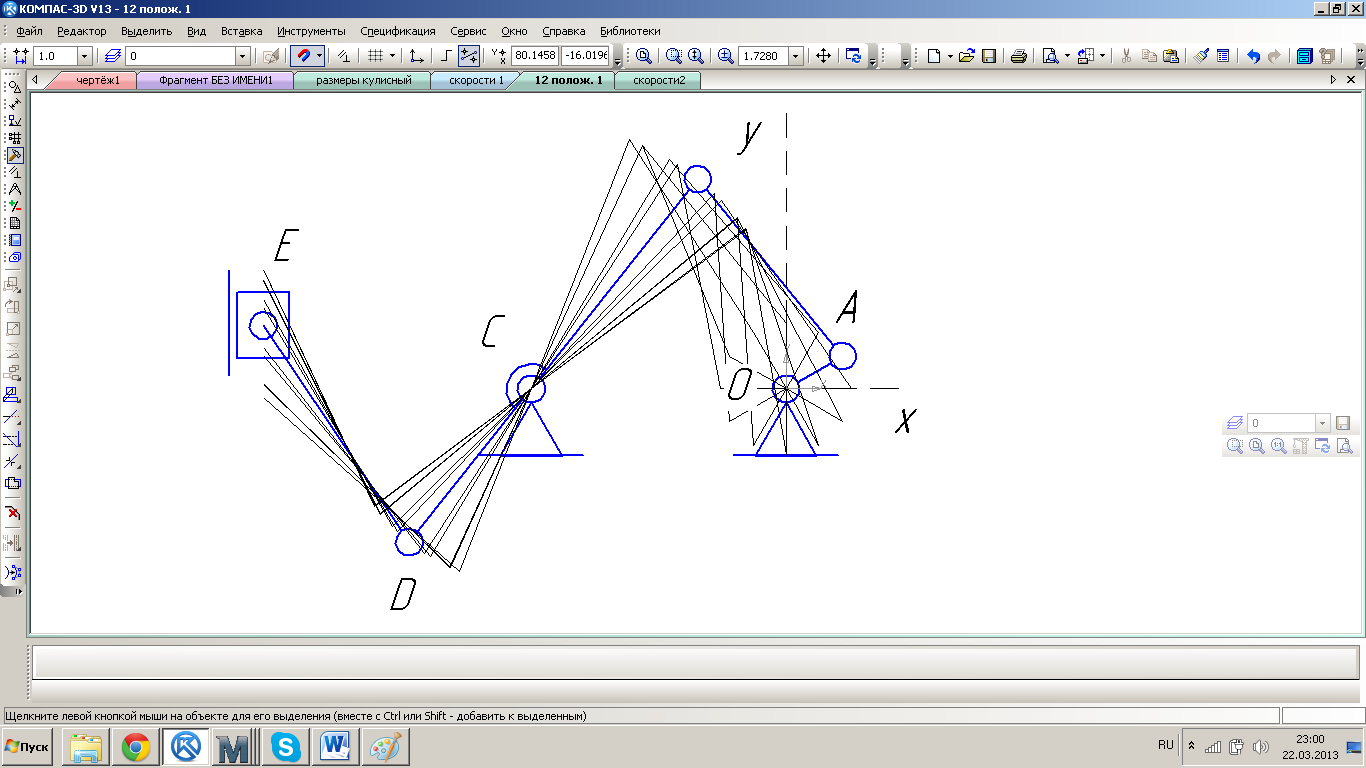
Рис.3.3. План 12-ти положений механизма №1
Прототип №2.
Групповые уравнения для группы ВПВ:
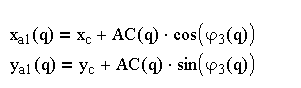(3.7)
Необходимые уравнения для определения функции положения 1-й группы:
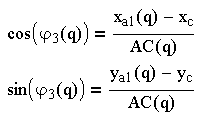(3.8)
Решением системы уравнений в общем виде определяются функции положения:
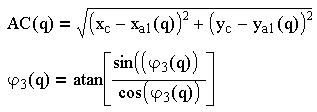(3.9)
Групповые уравнения для группы ВВП:
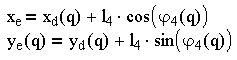(3.10)
Необходимые
уравнения для определения функции
положения 2-й группы: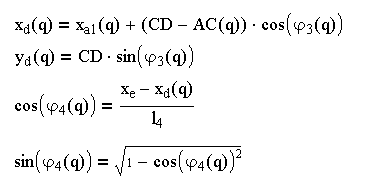 
(3.10)
Решением системы уравнений в общем виде определяются функции положения:
(3.11)
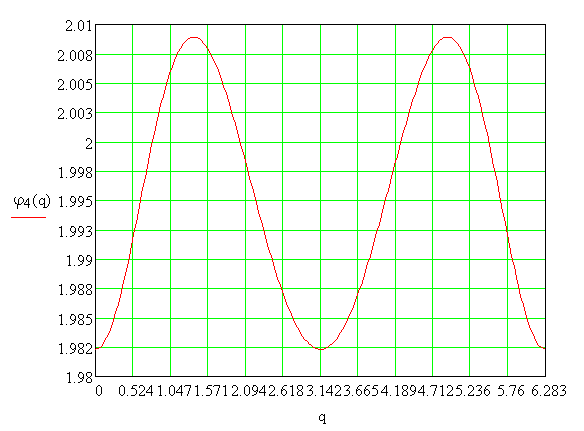
Рис.3.4. График функции положения φ4
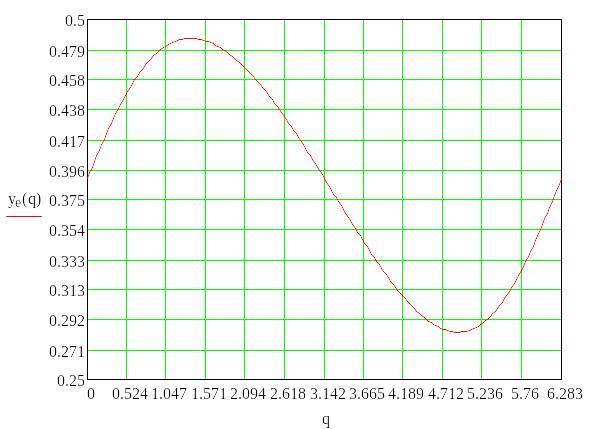
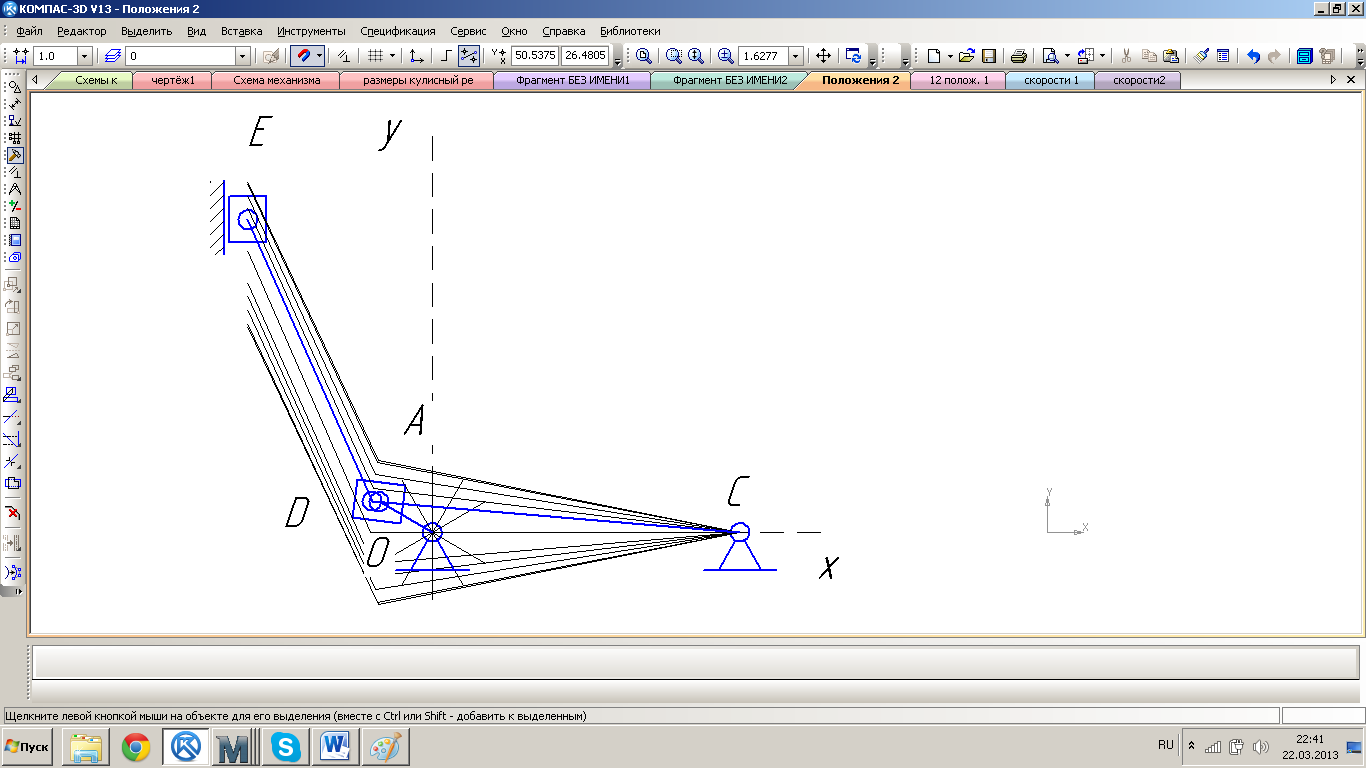
Рис.3.6. План 12-ти положений механизма №2
Выводы.
В результате геометрического анализа прототипов были определены координаты всех точек механизма, все углы между звеньями, а также построены графики функции положения. Результаты геометрического анализа необходимы для дальнейшего исследования механизмов.
Кинематический анализ механизмов
Задачи кинематического анализа механизмов
Целью кинематического анализа является определение скоростей и ускорений отдельных точек и звеньев рычажного механизма по известному закону входного звена.
Путём дифференцирования уравнения дважды по q уравнения геометрического анализа, находятся аналоги скоростей и ускорений механизма.
Графоаналитический метод кинематического анализа
При проведении кинематического анализа и построения планов скоростей и ускорений механизм №1 рассматривается в положении кривошипа 30° и в крайнем положении (122.4°).
Сумму векторов можно представить как:
Для нахождения скоростей берётся производная по времени от каждого полученного векторного уравнения:
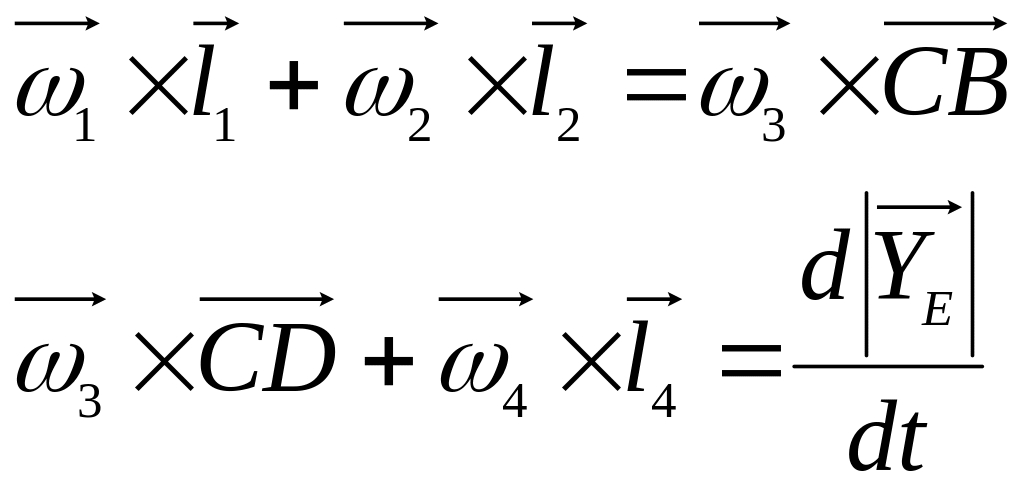
Полученные выражения можно представить в виде:
Построение плана скоростей при положении кривошипа 30°:
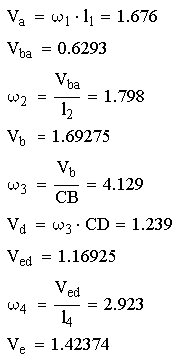
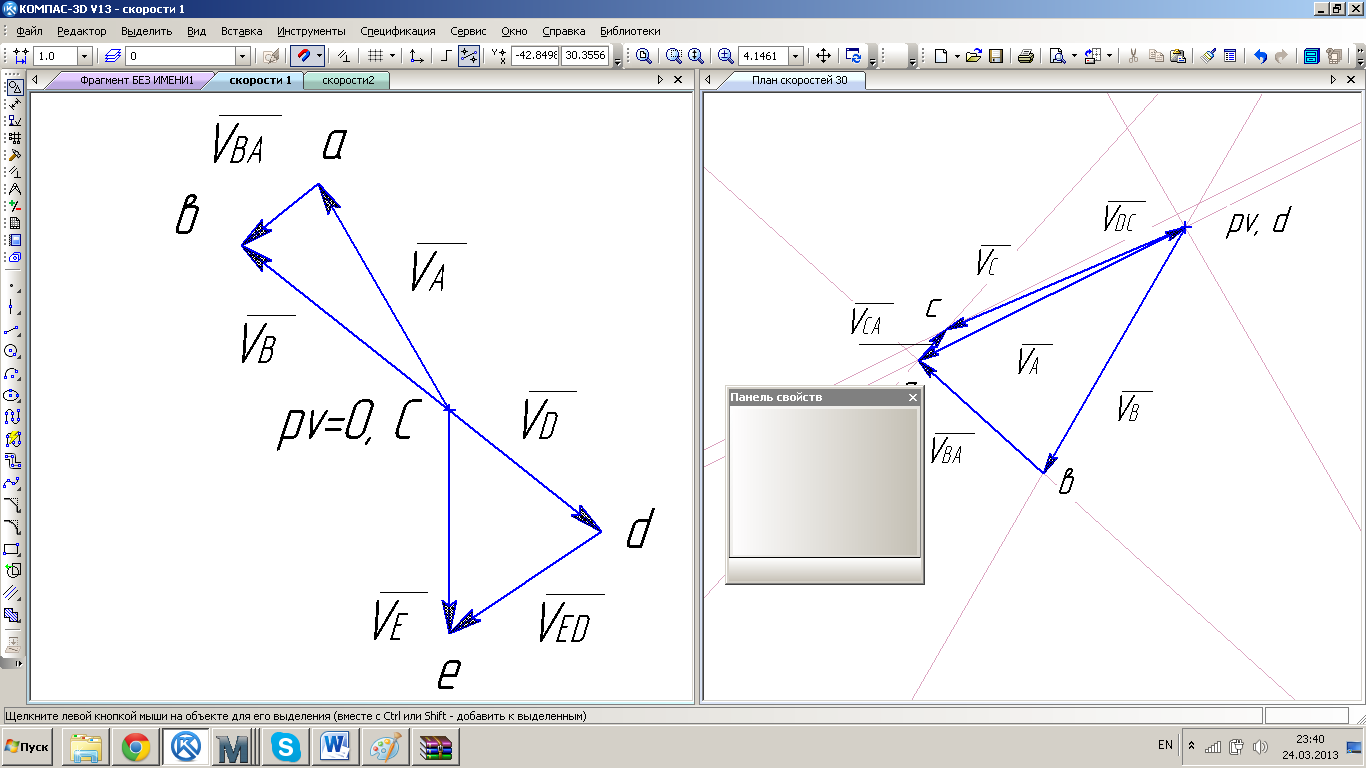
Рис.4.1. План скоростей для положения 30°
Построение плана скоростей для крайнего положения механизма:
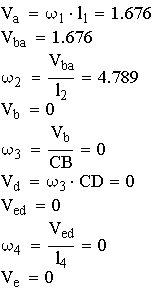
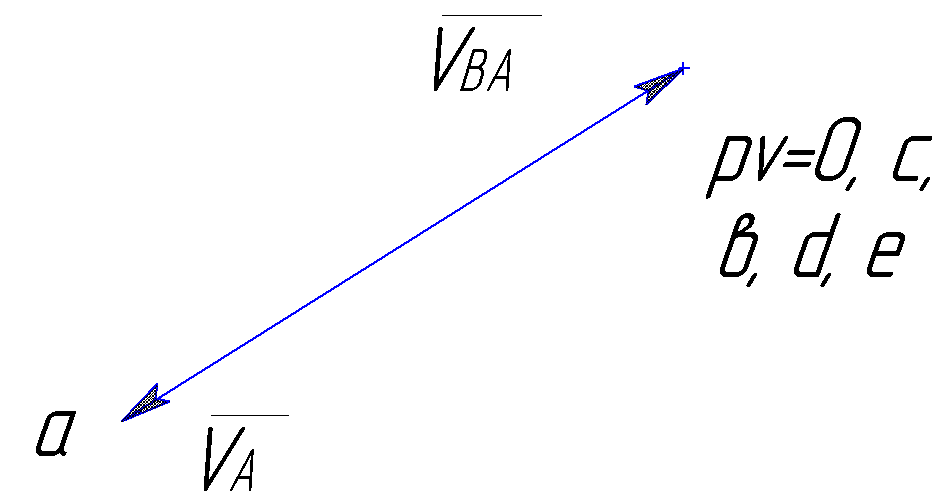
Рис.4.2. План скоростей для крайнего положения
Для нахождения ускорений берётся вторая производная по времени:
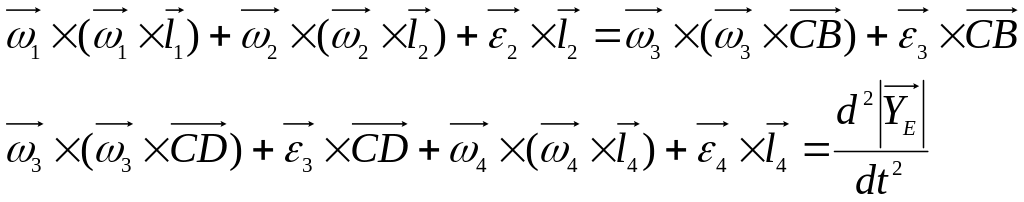
Выражения представляется в виде:
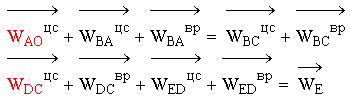
Построение плана ускорений при положении кривошипа 30°:
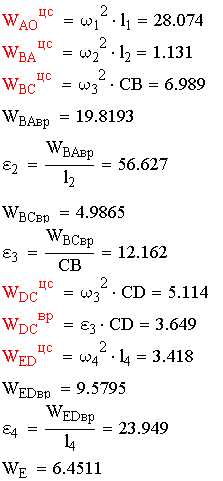
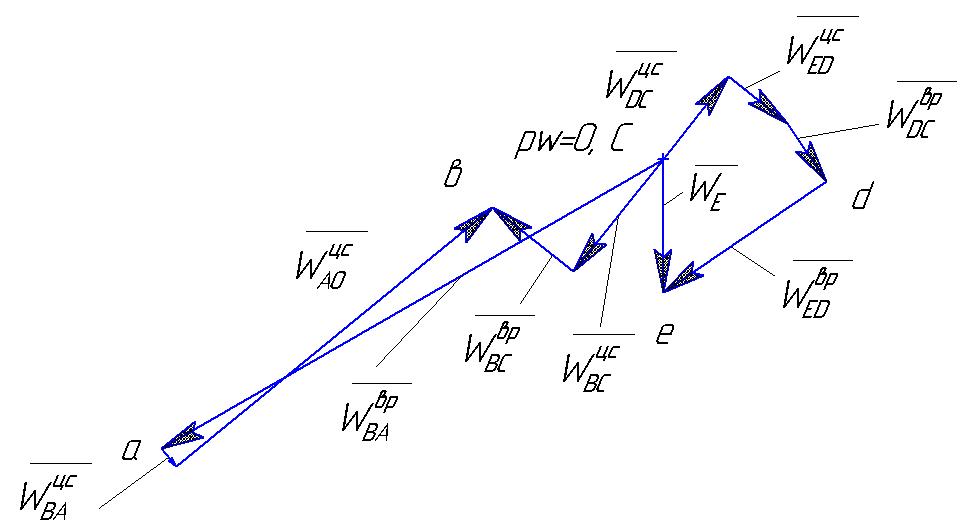
Рис.4.3. План ускорений для положения 30°
Построение плана ускорений для крайнего положения механизма:
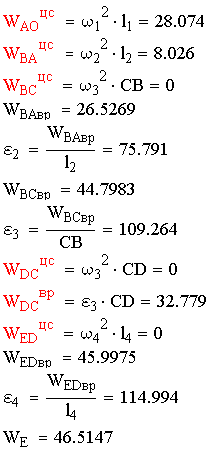
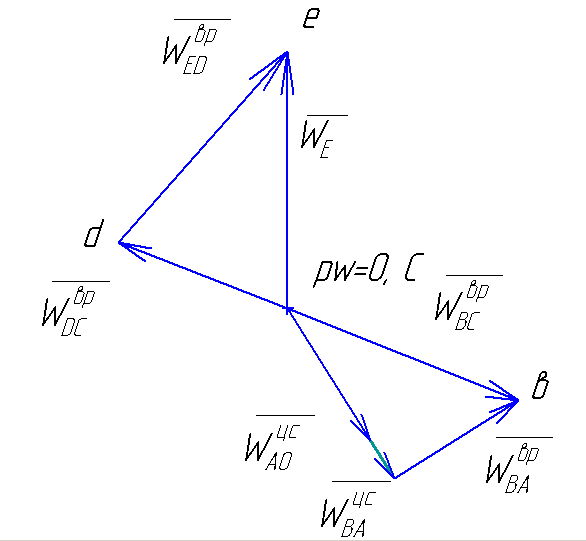
Рис.4.4. План ускорений для крайнего положения
При проведении кинематического анализа и построения планов скоростей и ускорений механизм №2 рассматривается в положении кривошипа 150° и в крайнем положении (78°).
Сумму векторов можно представить как:
Производная по времени от каждого полученного векторного уравнения:
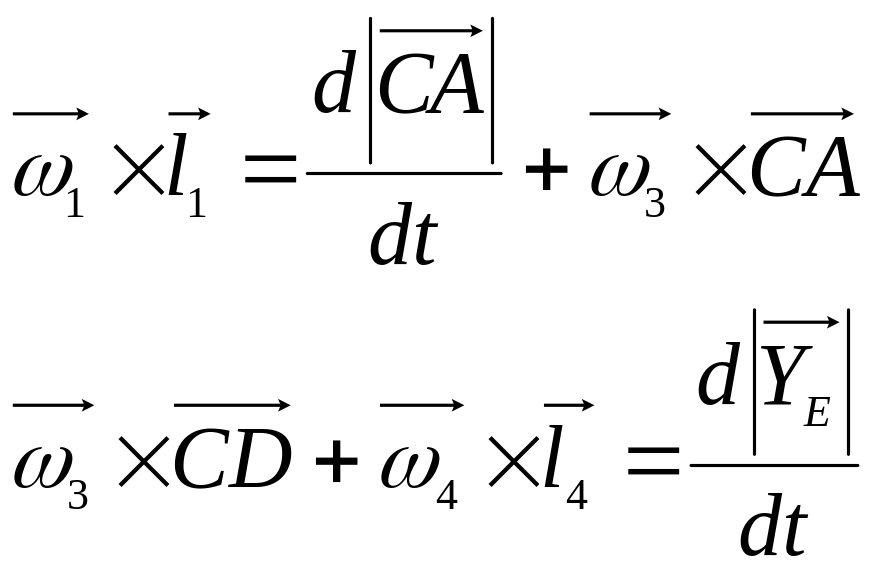
Полученные выражения можно представить в виде:
Построение плана скоростей в положении кривошипа 150°:
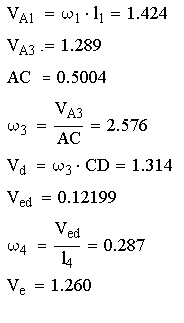
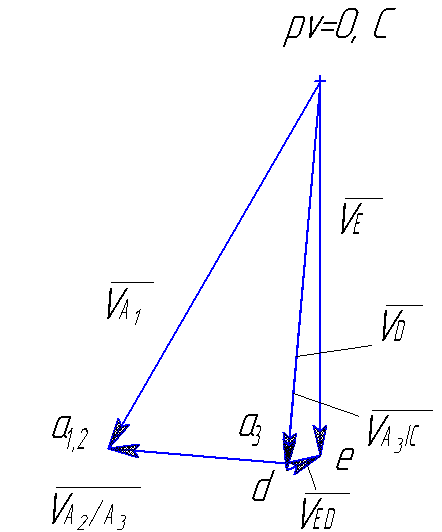
Рис.4.5. План скоростей для положения 30°
Построение плана скоростей для крайнего положения механизма:
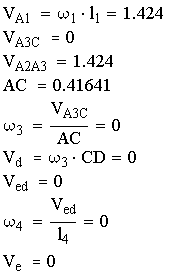
Рис.4.6. План скоростей для крайнего положения
Для нахождения ускорений берётся вторая производная по времени:
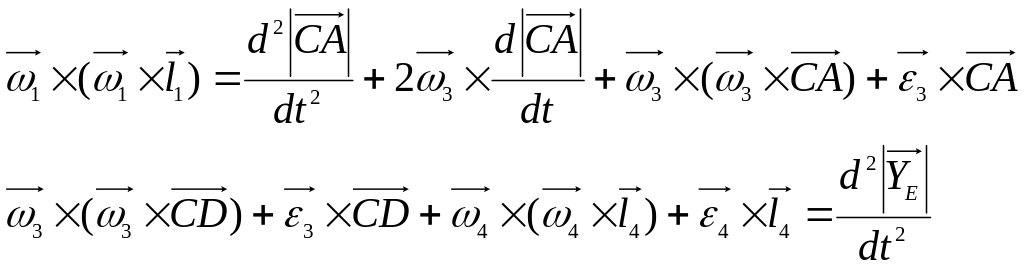
Выражения представляется в виде:
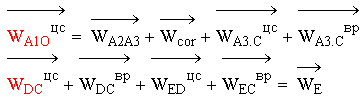
Построение плана ускорений при положении кривошипа 150°:
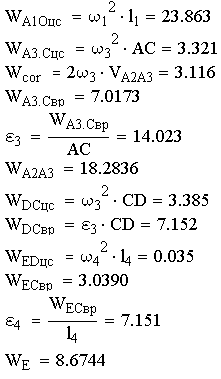
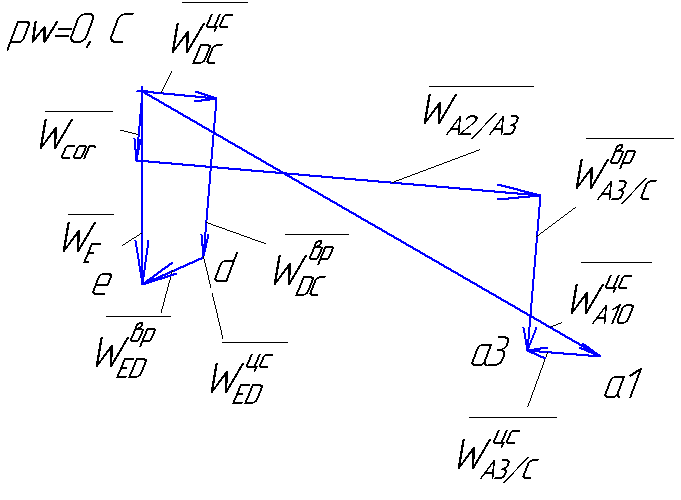
Рис.4.7. План ускорений для положения 30°
Построение плана ускорений для крайнего положения механизма:
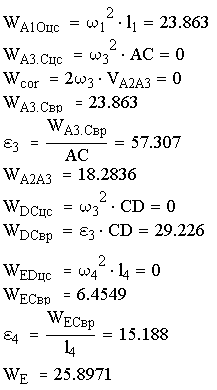
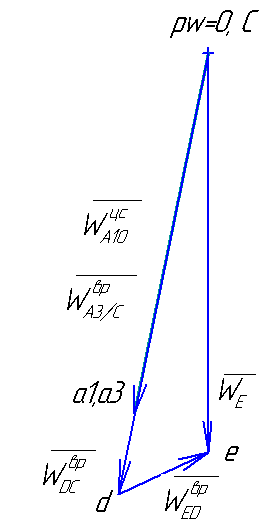
Рис.4.8. План ускорений для крайнего положения