3.2. Многокритериальные системы.

Для сложных систем получить критерий эффективности в виде скалярной функции не удается и приходиться иметь ело с векторным критерием. Такие системы называют многокритериальными. Для выбора наилучшего решения надо получить интегральную оценку, учитывающую оценки по всем компонентам векторного критерия. Для этого в простейшем случае применяют метод взвешенной суммы оценок критериев, в котором общая оценка

, где - весовой коэффициент, учитывающий вес - ой компоненты в общей оценке, 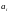- оценка, полученная для - ой компоненты. - число независимых компонент. Весовые коэффициенты обычно определяет экспертным путем.

Введение весовых коэффициентов позволяет получить линейную комбинацию компонент векторного критерия, переводя его тем самым в скалярную форму. Естественно, что введение линейных связей между независимыми по своей природе составляющими далеко не всегда дает удовлетворительное решение.

Достаточно эффективным способом, используемым в случаях векторного критерия, является выбор управляющих воздействий, оптимальных по Парето. Множество оптимальных по Парето решений с векторным критерием составляют такие решения, ни одно из которых не доминируемо в определенном смысле никаким другим решением из этого множества. Это означает, что множество управляющих воздействий, оптимальных по Парето, включает в себя практические несравнимые по скалярному критерию, т.е. такие, о которых нельзя однозначно сказать, какое из них лучше. Другими словами, какой из независимых критериев, являющихся компонентами векторного критерия, важнее с точки зрения общей оценки. Каждое из множества управляющих воздействий лучше любого другого по крайней мере по одному из независимых критериев, но в то же время хуже него по другим. Если множество по Парето содержит только одно управляющее воздействие, то оно является наилучшим по всем составляющим векторного критерия, т.е. по общей оценке.

Смысл оптимальности по Парето заключается в том, что выделяются только несколько решений, подлежащих дальнейшему рассмотрению, а все остальные исключаются. Количество оставшихся решений зависит от числа независимых компонент векторного критерия. Кроме того, оставшиеся решения легче сопоставить между собой, определенно зная, к какому ухудшению других компонент приводит оптимальность по одной из них. Этот выбор осуществляется уже не формальным образом и зависит от сознательного или интуитивного сравнения выигрыша по одним компонентам с проигрышем по другим.

3.3. Выбор критерия в состоянии неопределенности.

В системах управления часто приходится принимать решения в условиях неопределенности, чаще всего связанной с необходимостью принимать решения, не зная в какой ситуации оно будет реализовано. Зная, какие возможны ситуации и полный набор возможных решений, можно составить таблицу: в строках перечислить возможные решения, а в столбцах – ситуации, от которых зависит результат. В каждой клетке, на пересечении - ой строки и - го столбца, записываем некоторое число 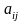- выражающее степень нашей удовлетворенности тем результатом, который, как предполагается, будет получен при выборе - ого решения, если реально осуществится - ая ситуация. В реальных системах число может представлять собой ожидаемые доход или убытки, пусть для определенности это будет доход.

Существует ряд подходов к решению этой задачи.

1. Лаплас предложил считать, что все возможные ситуации равновероятны и в этом случае выбирать решение так. Надо для каждого из возможных решений найти средний ожидаемый доход , суммируя в каждой строке и разделив полученную сумму на - число возможных ситуаций: = . Принимаем то решение, для которого максимально. Этот критерий хорош в том случае, когда решения надо принимать многократно, а составленный перечень ситуаций и решений почти не меняется. Если при этом ситуации будут чередоваться случайным образом, но каждая из них будет встречаться одинаково часто, то получим доход, близкий к наибольшему возможному среднему доходу. Однако очень маловероятно, что ожидаемые события равновероятны и будут встречаться с одинаковой частотой. В неблагоприятном случае можно много потерять, если будут встречаться ситуации, дающие при выбранном решении наименьший доход.

2. Чтобы обезопасить себя от таких неблагоприятных последствий, Вальд предложил для выбора решений другой критерий. Выберем в каждой строке самый маленький доход , а затем строку с наибольшим из этих минимальных доходов . Это и будет то решение, которое, по Вальду, следует принятью. Оно гарантирует в самой неблагоприятной ситуации получение наибольшего из минимальных доходов. Такой критерий называют максимином. Этот критерий очень осторожен выражает крайне пессимистическую точку зрения. А если ситуация окажется не самой неблагоприятной? Тогда наибольший доход может дать совсем другое решение.

3. Гурвиц предложил для принятия решений критерий, учитывающий индивидуальную степень оптимизма. Выберем в каждой строке самый маленький доход и самый большой . Введем коэффициент оптимизма , который может принимать значения от = 0 для полного пессимизма до = 1 для абсолютного оптимизма. Вычислим для каждой строки

значения величины = + (1 - ) . Принимаем то решение, которому соответствует строка с наибольшим значением .

Если принять = 0, критерий Гурвица переходит в критерий Вальда. При = 1 принимается решение обеспечивающее в благоприятной ситуации наибольший доход из всех возможных, но зато с большой степенью риска существенных потерь при других ситуациях. Промежуточные значения отражают степень оптимизма лица, принимающего решение, его надежды на благоприятную для него ситуацию.

Предложены и другие критерии. Например, критерий Сэвиджа - критерий минимального сожаления. Найдем для каждого из возможных состояний наиболее благоприятный случай, т.е. для каждого столбца выберем наибольший доход . Вычтем эту величину из всех данного столбца. Сэвидж называет полученную разность «сожалением» по поводу того решения, которое мы приняли, по сравнению с более доходным, которое мы могли принять, если бы заранее знали, какая ситуация возникнет. Все «сожаления» будут отрицательными. Выберем теперь в каждой строке минимальное «сожаление» (наибольшее по абсолютному значению) найдем строку с наибольшим из них. Принимая решение, соответствующее этой строке, мы гарантированы, что в наихудших условиях возможный убыток не превысит найденного значения, а в других случаях окажется еще меньше.

Итак, прежде чем выбрать решение, надо решить, какой критерий выбрать. Это наиболее ответственный вопрос для руководителя, так как именно в этом он имеет достаточную свободу выбора и именно в этом проявляются его характер, опыт и умение. Необходимо снижение степени неопределенности возможных ситуаций, для чего необходимо накопление статистических данных, позволяющих оценить вероятности каждой из ситуаций. Опыт прошлого может быть использован для оценки будущего. Если статистических данных нет, то значения вероятности каждой из ситуаций могут быть получены методами экспертных оценок.

Зная эти вероятности, можно для каждого решения найти математическое ожидание дохода = . То решение, для которого имеет наибольшее значение, является наиболее благоприятным в среднем решением.