7. Отыскание опорного решения основной задачи линейного программирования.

Пусть имеется ОЗЛП с ограничениями-равенствами, записанными в стандартной форме:

(7.1)

разрешенными относительно базисных переменных у₁,у₂,…,у_m, которые выражены через свободные переменные х₁,х₂,…,х _n. В каждой вершине ОРД (опорном решении) по крайней мере n переменных должны обращаться в нуль. Попробуем получить опорное решение, полагая в формулах (7.1) все свободные переменные равными нулю.

Имеем:

(7.2)

Если все свободные члены b₁,b₂,…,b_m в уравнениях (7.1) неотрицательны, это значит, что опорное решение уже получено; этот случай нас не интересует. Рассмотрим случай, когда среди свободных членов b₁,b₂,…,b_m есть отрицательные. Это значит, что решение (7.2) не является опорным – оно вообще не допустимо, и опорное решение еще предстоит найти. Для этого мы будем шаг за шагом обменивать местами базисные и свободные переменные в уравнениях (7.1) до тех пор, пока не придем к опорному решению или не убедимся, что его не существует. Последнее бывает в случае, когда система уравнений (7.1) несовместима с неравенствами

т.е. у нее нет неотрицательных решений.

Очевидно, нужно так обменивать местами базисные и свободные переменные, чтобы эта процедура приближала нас к границе ОДР, а не удаляла от нее, т.е. чтобы число отрицательных свободных членов с каждым шагом убывало, или, если число отрицательных свободных членов остается прежним, то, по крайней мере, убывали их абсолютные величины.

Пусть имеется одно из уравнений (7.1) с отрицательным свободным членом. Ищем в этой строке отрицательный элемент α_ij. Если такого элемента нет (все элементы α_ij≥0), это знак того, что система уравнений (7.1) несовместима с неравенствами (7.3). Действительно, при отсутствии отрицательных элементов в строке вся правая часть соответствующего уравнения может быть только отрицательной, а это противоречит условиям неотрицательности переменных.

Предположим, что отрицательный элемент есть. Тогда выбираем столбец, в котором он находится, в качестве разрешающего.

Теперь надо выбирать в этом столбце сам разрешающий элемент. Рассмотрим все элементы данного столбца, имеющие одинаковый знак со свободным членом. Из них выбираем в качестве разрешающего тот, для которого отношение к нему свободного члена минимально.

Таким образом, выбирается разрешающий столбец, разрешающий элемент в нем и, значит, разрешающая строка. А дальше идет табличная замена базисных переменных.

Стационарная транспортная задача

Симплекс – метод решения задач линейного программирования является универсальным и применим для решения любых таких задач. Однако существуют некоторые частные типы задач линейного программирования, которые в силу некоторых особенностей их структуры допускают решение более простыми методами. К ним относится, в частности транспортная задача.

Классическая транспортная задача линейного программирования формулируется следующим образом.

Имеется пунктов отправления: в которых сосредоточены запасы какого-то однородного товара (груза) в количестве соответственно

единиц. Кроме того, имеется пунктов назначения: 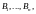подавших заявку соответственно на единиц товара. Предполагается, что сумма всех заявок равна сумме всех запасов: . Известна стоимость перевозки единицы товара от каждого пунктов отправления до каждого пункта назначения . Таблица (матрица) стоимостей перевозки задана

.

Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и при этом общая стоимость всех перевозок была минимальна. При такой постановке задачи показателем эффективности плана перевозок является стоимость; поэтому поставленную задачу точнее назвать транспортной задачей по критерию стоимости.

Дадим этой задаче математическую формулировку. Обозначим 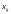- количество груза, отправляемого из пункта отправления в пункт назначения . Неотрицательные переменные должны удовлетворять следующим условиям:

1. Суммарное количество груза, направляемого из каждого пункта отправления во все пункты назначения, должно быть равно запасу груза в данном пункте. Это дает нам условий равенств:

2. Суммарное количество груза, доставляемого в каждый пункт назначения из всех пунктов отправления, должно быть равно заявке, поданной данным пунктом. Это дает нам условий равенств:

3. Суммарная стоимость всех перевозок должна быть минимальной, т.е. должен быть найден .

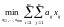Целевая функция линейна, ограничения-равенства также линейны. Перед нами – типичная задача линейного программирования с ограничениями-равенствами. Как и всякую другую задачу линейного программирования, ее можно было бы решить симплекс-методом, но данная задача имеет некоторые особенности, позволяющие решить ее более просто. Причиной является то, что все коэффициенты при переменных в ограничениях-равенствах равны 1. Кроме того, ограничения-равенства связаны одной линейной зависимостью, а именно, . Фактически из этих уравнений только -1 являются линейно независимыми. Значит ранг системы ограничений равен -1. А, следовательно, можно разрешить эти уравнения относительно -1 базисных переменных, выразив их через остальные, свободные. Подсчитаем количество свободных переменных. Оно равно:

= .

В задаче линейного программирования оптимальное решение достигается в одной из вершин ОДР, где по крайней мере переменных обращаются в нуль. Значит, в нашем случае для оптимального плана перевозок по крайне мере переменных должны быть равны 0.

Значения количества единиц груза, направляемых из пункта отправления в пункт назначения будем называть перевозками. Любую совокупность значений ( ) ( будем называть планом перевозок или просто планом.

План ( ) будем называть допустимым, если он удовлетворяет ограничениям-равенствам: все заявки удовлетворены, все запасы исчерпаны. Допустимый план будем называть опорным, если в нем отличны от нуля не более базисных перевозок , а остальные перевозки равны 0.

План ( ) будем называть оптимальным, если он, среди всех допустимых планов, приводит к наименьшей стоимости всех перевозок.

Перейдем к изложению методов решения транспортной задачи (ТЗ).Эти методы сводятся к более простым операциям с таблицей, где в определенном порядке записаны все условия ТЗ. Такую таблицу будем называть транспортной таблицей. В ней записываются:

- пункты отправления и назначения,

- запасы, имеющиеся в пунктах отправления,

- заявки, поданные пунктами назначения,

- стоимости перевозок из каждого пункта отправления в каждый пункт назначения.

Стоимости перевозок будем помещать в правом верхнем углу каждой ячейки с тем, чтобы в смой ячейке при составления плана помещать перевозки . Образец транспортной таблицы

ПО / ПН			…………..		Запасы
			……………..
			……………..
………….	…………….	……………	…………..	……………	…………..
			……………
Заявки			……………..

Ранг системы ограничений-уравнений равен , где - число строк, - число столбцов транспортной таблицы. В каждом опорном плане будут отличны от нуля не более перевозок. Ячейки таблицы, в которых будем записывать отличные от нуля перевозки, называются базисными, а остальные (пустые) свободными.

Решение ТЗ сводится к следующему.Надо найти такие значения положительных перевозок, которые, будучи проставлены в базисных клетках транспортной таблицы, удовлетворяли следующим условиям:

- сумма перевозок в каждой строке таблицы должна быть равна запасу данного ПО,

- сумма перевозок в каждом столбце должна быть равна заявке данного ПН,

- общая стоимость перевозок – минимальная.

В дальнейшем все действия по нахождению решения ТЗ будут сводиться к преобразованию транспортной таблицы. При описании этих преобразований удобно пользоваться нумерацией клеток таблицы. Клеткой (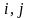 ) называется клетка, стоящая в - ой строке и -ом столбце транспортной таблицы.