Глава 1. Метод неопределенного множителя Лагранжа
Общая постановка оптимальной задачи с одним ограничением
Имеется
дифференцируемая функция
.
Надо найти ее минимум при ограничении
= 0. В соответствии с методом неопределенных
множителей Лагранжа задача сводится в
этом случае к введению переменной
и решению следующей оптимальной задачи
безусловной оптимизации: найти
,
где
=
-
.
В соответствии с
теоремой 2 в качестве области
можно взять
область, описываемую следующими
неравенствами
,
и функция
должна быть выпукла в области
.
Из теоремы 2 следует требование выпуклости
функции
только в окрестности точки экстремума
.
В соответствии с этой теоремой надо
найти критическую (стационарную) точку
и проверить выпуклость функции
в окрестности этой точки.
Тогда по теореме 2 решение этой оптимальной задачи сводится к решению следующей системы в общем виде нелинейных уравнений
=
-
= 0,
,
,
(1)
= = 0. (2)
Нашей целью является найти те классы функций и , для которых возможно получение аналитических решений, чтобы дать в руки читателей аппарат получения аналитических решений оптимальных задач.
Для удовлетворения условия величина должна иметь знак, равный
-
).
(3)
Сепарабельность целевой функции и функции – ограничения. Общий алгоритм решения
Справедливо следующее утверждение: если все частные функции сепарабельной функции в точке , являются выпуклыми, то и сама функция является выпуклой в точке . Оно следует из определения определителя матрицы Гессе. Обратное утверждение неверно.
Частная функция в точке является выпуклой, если её вторая производная в этой точке неотрицательна.
Пусть
целевая функция и функция – ограничение
являются сепарабельными [ ] по своим
переменным, т.е. представляются в
следующем виде:
=
,
=
-
,
.
Тогда система нелинейных уравнений
(1-2) п. 1 в этом случае приобретает вид
-
= 0,
,
(1)
= , . (2)
Замечание 2.1. В (1) знак – поставлен перед для случая, когда ) = +. В противном случае надо поменять знак на противоположный.
Алгоритм нахождения решения в области сводится к следующему:
1)
из (1) надо найти формулу, выражающую
через
,
т.е.
=
(
),
имеем
/
=
.Требования
к функции
/
:
она должна быть монотонной, чтобы
существовала обратная функция к ней,
тогда
(
)
как раз и будет такой обратной функцией;
2) подставить выражение = ( ) в (2), в результате получаем уравнение
=
,
,
(3)
3) из уравнения (3) находим ,
4)
подставляем найденное выражение для
в формулу
=
(
),
тем самым, получаем оптимальную точку
),
5)
проверяем условия
,
и
,
где
- малая величина,
6) если условия 5) выполняются, то точка ) дает минимум целевой функции в области , т.е. будет являться решением поставленной оптимальной задачи.
Теорема
3. Пусть
функция
факторизуема
в виде
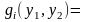
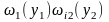и
для
/
справедливо
представление
/
=
=
,
где функция
не зависит от
,
и обратная функция
=
факторизуема в виде
,
то оптимальное решение имеет следующий
вид
=
(
),
(4)
где
- обратная функция от функции
.
Доказательство.
Из равенства
=
находим
,
тогда из факторизации
следует, что
представляется в виде
.
Подставляя это выражение в (2), получаем
=
)
=
=
,
(5)
откуда
имеем
=
(
или
(
),
(6)
где - обратная функция от функции . Подставляя это выражение в формулу для , приходим к (4). Теорема 3 доказана.
Рассмотрим последовательно случаи, когда возможно получение аналитического решения оптимальных задач с использованием метода неопределенного множителя Лагранжа.