
- •1.2. Условия существования управления.
- •1.3. Оптимальность управления.
- •Лекция 2
- •2.1. Этапы принятия решений
- •2.2. Схема функционирования системы управления
- •2.3. Цели и критерии эффективности.
- •Лекция 3
- •3. 1. Виды критериев.
- •3.2. Многокритериальные системы.
- •3.3. Выбор критерия в состоянии неопределенности.
- •3.4. Выявление целей и критериев.
- •3.5. Особенности построения модели управляемой системы
- •4.1. Методология и психологические аспекты принятия решений
- •4.2. Системный анализ.
- •4.3. Таблицы решений.
- •Лекция 5. Принятие решений в различных условиях.
- •5.1.Принятие решений в разомкнутых системах
- •5.2. Управление в системах с обратной связью.
- •5.3. Условия внешней среды.
- •Принятие решений в условиях определенности
- •Принятие решения в условиях риска
- •Принятие решений в условиях неопределенности
- •Принятие решений в конфликтных ситуациях
- •Лекция 6. Принятие решений и информация
- •Основные характеристики информации.
- •Лекция 7. Минимизация функции одной переменной без ограничений
- •1.1. Постановка задачи
- •1.2. Полином произвольной степени
- •1.3. Степенная функция, умноженная на экспоненциальную функцию
- •Лекция 8. 1.4. Частный случай полинома, умноженного на экспоненциальную функцию
- •1.5. Степенная функция, умноженная на экспоненциальную функцию, зависящую от полинома второй степени
- •Минимизация функции нескольких переменных без ограничений
- •2.1. Постановка задачи
- •2.2. Детализация достаточных условий экстремума.
- •Лекция 9. 2.3. Сепарабельные функции
- •2.4. Факторизованные функции
- •2.5. Сумма квадратов переменных
- •2.6. Квадратичная форма
- •2.7. Частный случай кубической формы от двух переменных
- •Частный случай кубической формы от произвольного количества переменных
- •Частный случай полинома произвольной степени от двух переменных
- •Методы условной оптимизации
- •Задача нелинейного программирования. Метод неопределенных множителей Лагранжа
- •Глава 1. Метод неопределенного множителя Лагранжа
- •Общая постановка оптимальной задачи с одним ограничением
- •Сепарабельность целевой функции и функции – ограничения. Общий алгоритм решения
- •3. Степенные функции с одинаковыми степенями частных функций
- •2. Основная задача линейного программирования.
- •3. Геометрическая интерпретация основной задачи линейного программирования.
- •Задача линейного программирования с ограничениями-неравенствами. Переход от нее к озлп и обратно
- •5. Симплекс-метод решения задач линейного программирования Алгоритм поиска опорного и оптимального решения
- •6. Табличный метод замены базисных переменных.
- •Отыскание опорного решения основной задачи линейного программирования.
- •Стационарная транспортная задача
- •Нахождение опорного плана
- •Поиск оптимального плана, метод последовательного улучшения плана для стационарной транспортной задачи
1.3. Степенная функция, умноженная на экспоненциальную функцию
Пусть функция ) является степенной функцией, умноженной на экспоненциальную функцию со степенью в виде линейной функции, т.е.
)
=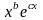 .
Имеем
)
=
.
Имеем
)
=
 ,
откуда определяются две конечные
стационарные точки:
= -
,
откуда определяются две конечные
стационарные точки:
= -
 и
и
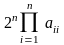 = 0 при
= 0 при
 .
Вторая производная
)
от
)
равна
)
=
.
Вторая производная
)
от
)
равна
)
=
 и в стационарной точке
= -
равна
-
)
= -
и в стационарной точке
= -
равна
-
)
= - (-
(-
 ,
а в стационарной точке.
,
а в стационарной точке.
 = 0 при
= 0 при
 -
)
равна 0, при
-
)
равна 0, при
 равна
равна
 .
Поэтому необходимо рассмотреть только
стационарную точку
.
Поэтому необходимо рассмотреть только
стационарную точку
 = -
.
= -
.
Рассмотрим последовательно все возможные ситуации.
1.
 принимает целочисленные конечные
значения,
принимает целочисленные конечные
значения,
 принимает конечные значения. В этом
случае
-
)
является конечным числом со знаком -,
если
- четное, и знаком +, если
- нечетное. Таким образом, если
- четное, то имеем максимум и, если
- нечетное, то минимум. Если же
принимает дробные конечные значения,
то
принимает конечные значения. В этом
случае
-
)
является конечным числом со знаком -,
если
- четное, и знаком +, если
- нечетное. Таким образом, если
- четное, то имеем максимум и, если
- нечетное, то минимум. Если же
принимает дробные конечные значения,
то
 -
)
неопределенна, так как принимает
комплексные значения.
-
)
неопределенна, так как принимает
комплексные значения.
2.
 .
В этом случае
-
)
является конечным числом со знаком -,
т.е. имеем максимум.
.
В этом случае
-
)
является конечным числом со знаком -,
т.е. имеем максимум.
3.
 .
В этом случае
-
)
является конечным числом со знаком +,
т.е. имеем минимум.
.
В этом случае
-
)
является конечным числом со знаком +,
т.е. имеем минимум.
4.
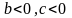 ,
,
 принимает целочисленные конечные
значения. В этом случае
-
)
является конечным числом со знаком +,
если
- четное, и знаком -, если
- нечетное. Таким образом, если
- четное, то имеем минимум и, если
- нечетное, то максимум. Если же
принимает целочисленные конечные
значения. В этом случае
-
)
является конечным числом со знаком +,
если
- четное, и знаком -, если
- нечетное. Таким образом, если
- четное, то имеем минимум и, если
- нечетное, то максимум. Если же
 принимает дробные конечные значения,
то
-
)
неопределенна, так как принимает
комплексные значения.
принимает дробные конечные значения,
то
-
)
неопределенна, так как принимает
комплексные значения.
Лекция 8. 1.4. Частный случай полинома, умноженного на экспоненциальную функцию
Рассмотрим
функцию
)
следующего вида
)
= ( .
Имеем
)
=
.
Имеем
)
=
 = 0, откуда
определяются три конечные стационарные
точки:
= 0, откуда
определяются три конечные стационарные
точки:
 ,
,
 при выполнении неравенства
при выполнении неравенства
 и
и
 при
.
Вторая производная
)
от
)
равна
)
=
при
.
Вторая производная
)
от
)
равна
)
=

 +
+
 (
(![]()
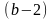
 .
Она в стационарной
точке
.
Она в стационарной
точке
 при
при
 равна 0, при
равна 0, при
 равна
,
при
равна
,
при
 неопределенна, т.е. в точке
функция
)
не имеет экстремума.
неопределенна, т.е. в точке
функция
)
не имеет экстремума.
Поэтому
остается рассмотреть возможные значения

 )
в точках
)
в точках
 =
и
=
и
 =
.
В зависимости от исходных данных
=
.
В зависимости от исходных данных
 корни
и
могут принимать разные значения. Имеем
следующие случаи:
корни
и
могут принимать разные значения. Имеем
следующие случаи:
1.
.
В этом случае
и
являются действительными числами. Если
)
,
то
является точкой минимума для функции
).
Если
)
 ,
то
является точкой максимума для функции
).
Если
)
= 0, то
не является точкой экстремума для
функции
).
Эти же выводы справедливы и для точки
.
,
то
является точкой максимума для функции
).
Если
)
= 0, то
не является точкой экстремума для
функции
).
Эти же выводы справедливы и для точки
.
2.
 .
В этом случае
и
являются комплексными числами и они не
являются точками экстремума для функции
).
.
В этом случае
и
являются комплексными числами и они не
являются точками экстремума для функции
).
1.5. Степенная функция, умноженная на экспоненциальную функцию, зависящую от полинома второй степени
Пусть функция
)
является
степенной
функцией, умноженной на экспоненциальную
функцию со степенью в виде полинома
второй степени, т.е.
)
= .
Имеем
)
=
.
Имеем
)
=
 = 0
= 0

 = 0
= 0
 = 0 , откуда
определяются три конечные стационарные
точки:
= 0 , откуда
определяются три конечные стационарные
точки:
 ,
,
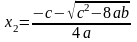 при
при
 и
и
 = 0 при
.
Вторая производная
)
от
)
равна
)
=
= 0 при
.
Вторая производная
)
от
)
равна
)
=
 (
( +
+ ).
).
Вторая производная
)
в точке
= 0 равна 0 при
 ,
при
,
при
 неопределенна, при
равна
,
т.е. точка
= 0 не является точкой экстремума для
).
неопределенна, при
равна
,
т.е. точка
= 0 не является точкой экстремума для
).
Поэтому остается рассмотреть возможные значения ) в точках = и = . В зависимости от исходных данных корни и могут принимать разные значения. Имеем следующие случаи:
1. . В этом случае и являются действительными числами. Если ) , то является точкой минимума для функции ). Если ) , то является точкой максимума для функции ). Если ) = 0, то не является точкой экстремума для функции ). Эти же выводы справедливы и для точки .
2.
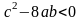 .
В этом случае
и
являются комплексными числами и они не
являются точками экстремума для функции
).
.
В этом случае
и
являются комплексными числами и они не
являются точками экстремума для функции
).
