10.4 Закон сложения скоростей в релятивистской механике
Положение
материальной точки в неподвижной системе
координат в каждый момент времени t
определяется значением x,
y,
z.
Проекции вектора скорости на координатные
оси равны:
 ,
,
 ,
,
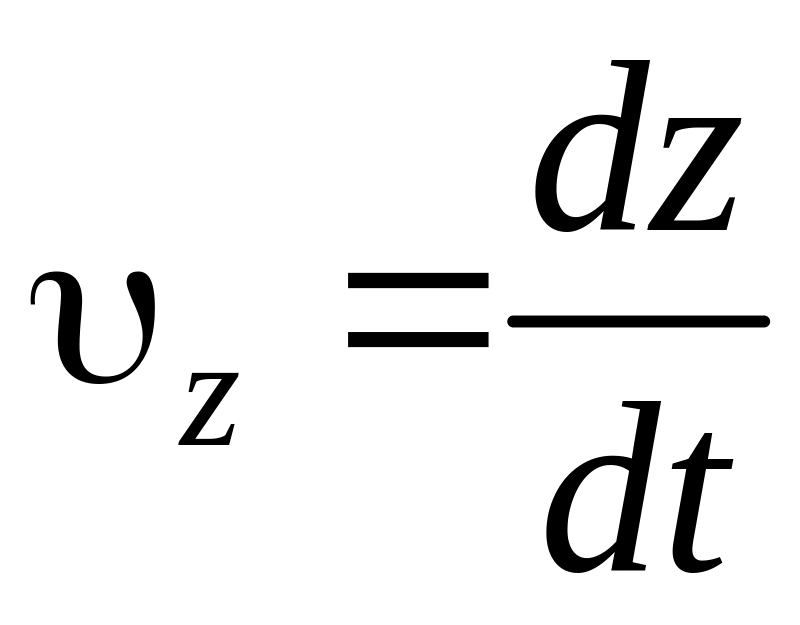 .
.
В системе К
положение точки в момент времени t
определяется координатами x,
y,
z.
Проекция на оси x,
y,
z
вектора скорости относительно систем
К :
 ,
,
 ,
,
 .
.
Из преобразования
Лоренца (10.6) следует:
 ,
,
 ,
,
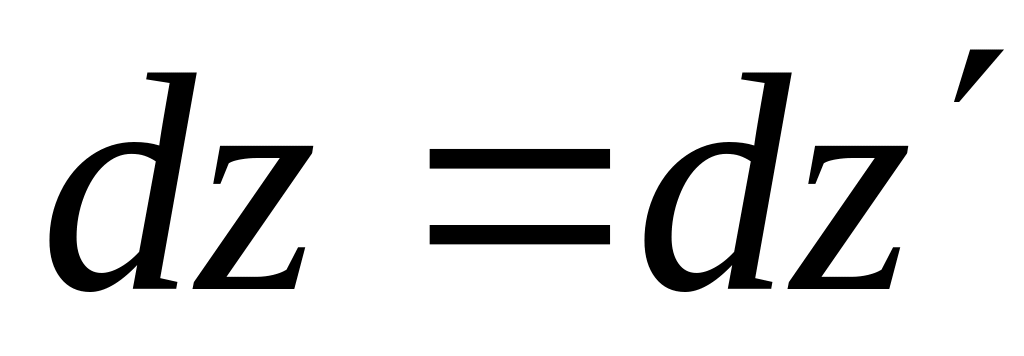 ,
,
 .
.
Разделив первые
три равенства на четвертое, получим
формулы преобразования скоростей в
релятивистской механике:
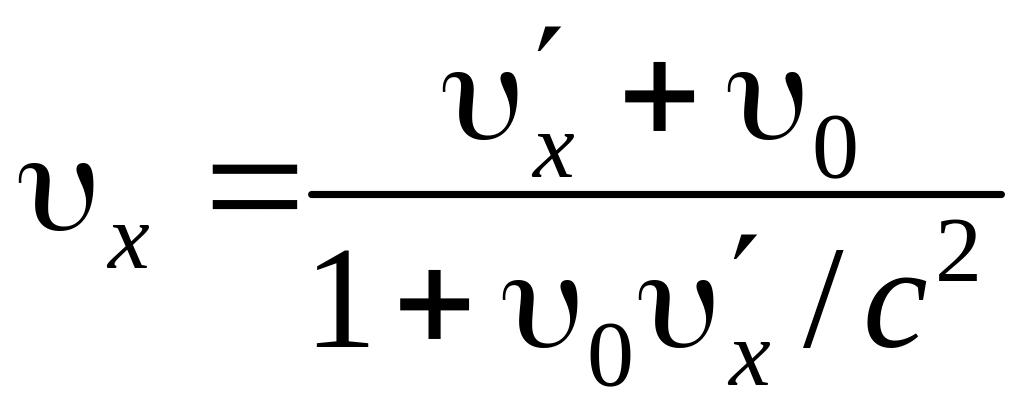 ,
,
 ,
,
 .
(10.9)
.
(10.9)
Если 0
<< c,
то соотношения (10.9) переходят в формулы
сложения скоростей в классической
механике.
Если тело движется
параллельно оси х,
его скорость
относительно системы К
совпадает с x
и равна:
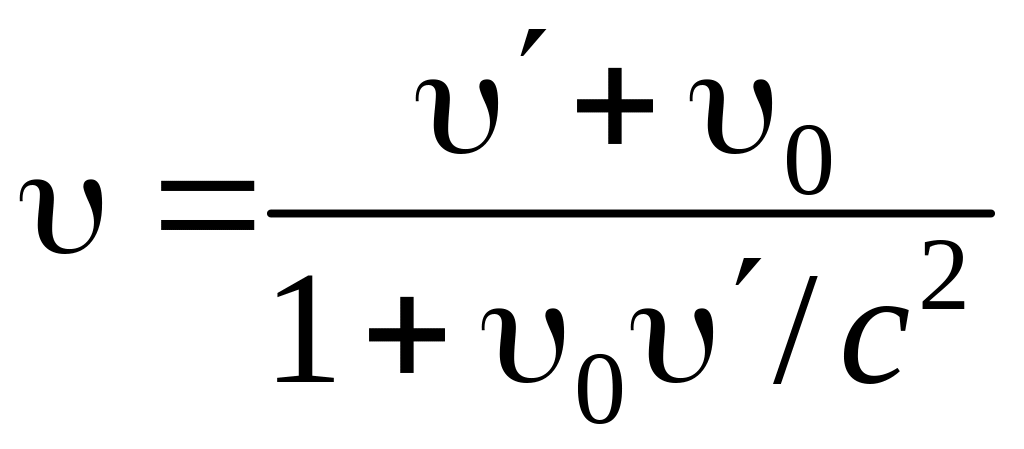 .
(10.10)
.
(10.10)
Пусть
равна с.
Тогда скорость
по формуле (10.10) равна
 .
.
Полученное
соотношение утверждает, что скорость
тела равна скорости света с,
что подтверждает второй постулат
Эйнштейна.


 ,
,
 .
.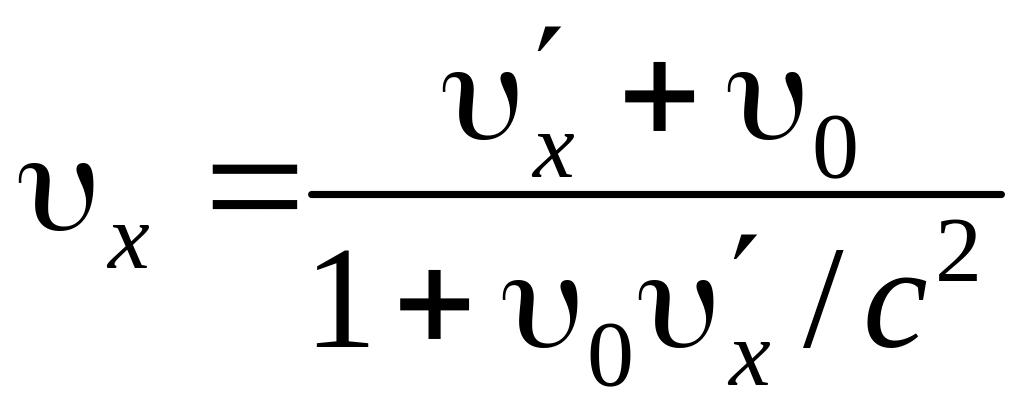 ,
,
 ,
,
 .
(10.9)
.
(10.9)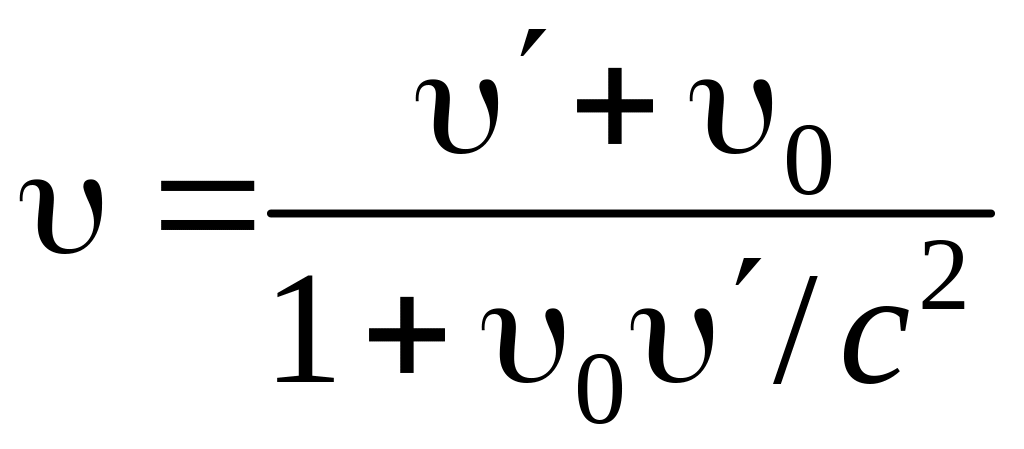 .
(10.10)
.
(10.10) .
.