Ограниченность законов классической механики

С развитием науки обнаружились новые факты, которые не укладывались в рамки классической механики – обнаружено постоянство скорости света. Оказалось, что независимо от скорости движения источников и приемников света скорость света в вакууме одинакова во всех инерциальных системах отсчета и равна величине c=2,998 ∙10⁸ м/с.

Подверглись радикальному пересмотру ньютоновские представления о пространстве и времени, а также постулаты классической механики - создана “механика больших скоростей” - релятивистской механики.

Преобразования Галилея

В основе классической механики лежит принцип относительности Галилея.

Р ассмотрим две инерциальные системы отсчета К и К , причем система рис. 10.3

отсчета К  движется относительно системы К с постоянной скоростью . Связь между координатами x, y, z некоторой точки М в системе К и координатами x , y , z  той же точки в системе К , как следует из рис. 10.3, будет иметь вид:

, , , . (10.14)

Уравнения (10.14) называются преобразованиями Галилея.

Продифференцировав соотношения (10.14) по времени, найдем связь между скоростями точки М по отношению к системам отсчета К и К :

(10.15)

Или в векторной форме:

. (10.16)

Полученные соотношения (10.15) и (10.16) представляют собой правило сложения скоростей в классической механике.

Продифференцировав соотношение (10.16) по времени, получим

. (10.17)

Из равенства (10.17) следует, что ускорение в инерциальных системах отсчета К и К  одинаково.

Отсюда согласно второму закону Ньютона вытекает, что силы, действующие на тело в инерциальных системах отсчета, также будут одинаковыми. Поэтому, уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой.

Этот вывод является математическим выражением механического принципа относительности Галилея: в любых инерциальных системах отсчета все механические явления при одних и тех же условиях протекают одинаково.

Постулаты Эйнштейна

Эйнштейном были сформулированы постулаты специальной теории относительности, т.е. наиболее бесспорные предположения, принятые без доказательств:

1) в любых инерциальных системах отсчета все физические явления (механические, электромагнитные и др.) при одних и тех же условиях протекают одинаково; иначе говоря, с помощью любых опытов, проведенных в замкнутой системе тел, нельзя обнаружить, покоится эта система или движется равномерно и прямолинейно;

2) Скорость света в вакууме не зависит от скорости движения источника света; она одинакова во всех направлениях и во всех инерциальных системах отсчета. Преобразования Лоренца и их следствия

Эйнштейн показал, что в соответствии с двумя постулатами теории относительности связь между координатами и временем в двух инерциальных системах отсчета К и К , изображенных на рис. 10.3, выражается не преобразованием Галилея (10.1), а преобразованием Лоренца:

, (10.18)

или

, (10.19)

где .

В основу вывода этих формул было положено условие равноправности всех систем отсчета, согласно которому преобразования должны быть линейными.

Из преобразований (10.19), следует, что при ₀ << c оно совпадает с преобразованиями Галилея .

Рассмотрим следствия из преобразований Лоренца.

а) Одновременность событий в разных системах отсчета.

Пусть в системе К в точках с координатами x₁ и x₂ происходят одновременно два события в момент времени . Согласно (10.6) в системе К^/ этим событиям будут соответствовать координаты

и

и моменты времени

и .

Анализ приведенных соотношений показывает, что если события в системе К происходят в одном и том же месте (x₁ = x₂), то они будут совпадать в пространстве и будут одновременными в системе К . Если же в системе К события пространственно разнесены , то в системе К  они также пространственно разобщены , но не будут одновременными .

б) Длина тел в различных системах.

Пусть стержень расположен вдоль оси х и покоится относительно системы К . Длина его в этой системе равна , где и ‑ не изменяющиеся со временем t координаты концов стержня. Относительно системы К стержень движется со скоростью ₀. Для определения его длины в этой системе отметим координаты концов x₁ и x₂ в один и тот же момент времени t₁ = t₂ = b. Тогда длина стержня в системе К равна l = x₂ – x₁ . Из преобразований Лоренца следует

.

Тогда, длина стержня в системе К  равна , или

. (10.7)

Таким образом, длина стержня l, измеренная в системе, относительно которой он движется, отказывается меньше длины l₀, измеренной в системе, относительно которой стержень покоится. Отметим, что в направлении осей у и z размеры стержня одинаковы во всех системах отсчета.

в) Длительность событий в различных системах.

Пусть в точке, неподвижной относительно системы К , происходит событие длительностью . Поскольку событие происходит в точке, то . Относительно системы К точка, в которой происходит событие перемещается со скоростью ₀. Согласно преобразованиям Лоренца началу и концу события в системе К соответствуют моменты времени t₁ и t₂, которые равны

, .

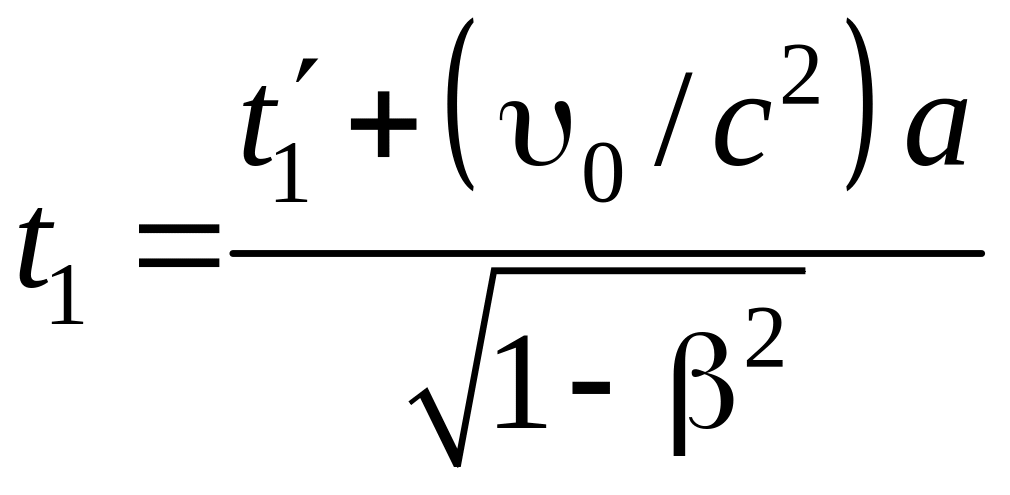Временной интервал между событиями в этой системе равен

.

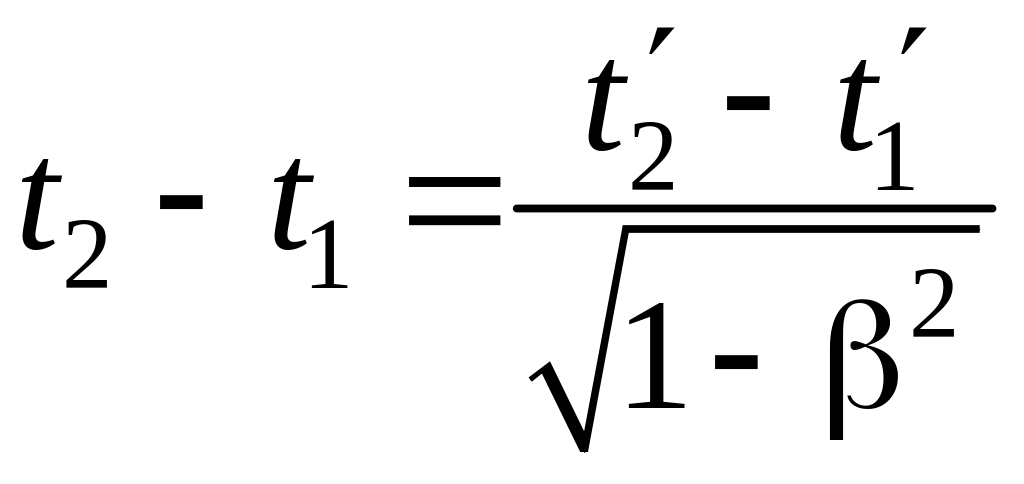Обозначим t₂ – t₁ = t. Тогда

. (10.8)

Из (10.8) следует, что t, определенное по часам, движущимся относительно покоящейся системы, больше t₀ , измеренной по часам, неподвижным относительно системы. Согласно (10.8) t₀ < t, откуда следует, что движущиеся части идут медленнее, чем покоящиеся часы.

Время t₀ , отсчитанное по часам, движущимся вместе с телом, называется собственным временем этого тела. Собственное время одинаково во всех инерциальных системах.