Лекция 10 Плотность потока энергии волны. Вектор Умова

Плотностью потока энергии волны называется вектор , направленный в сторону распространения волны и численно равный отношению потока энергии dΦ, сквозь малый элемент dS поверхности к площади dS_n проекции этого элемента на плоскость, перпендикулярную к направлению распространения волны:

.

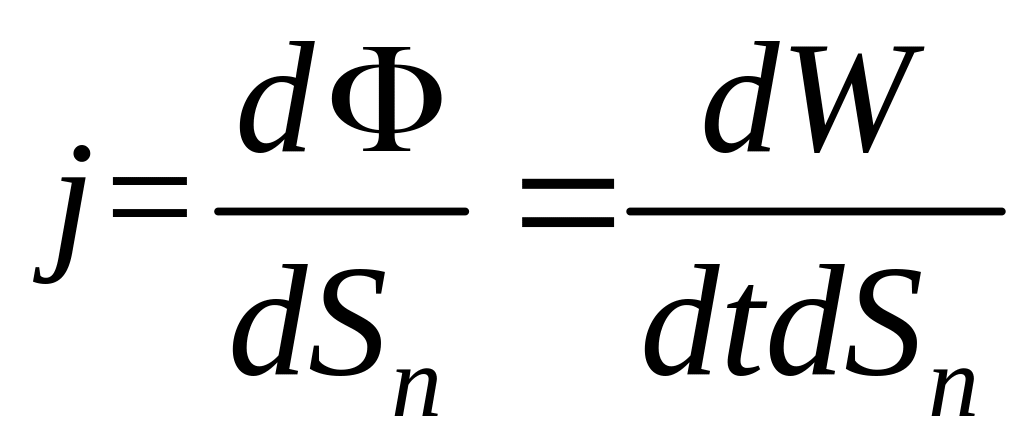Выразим плотность потока энергии через объемную плотность энергии w. Согласно определению, плотность потока энергии волны равна

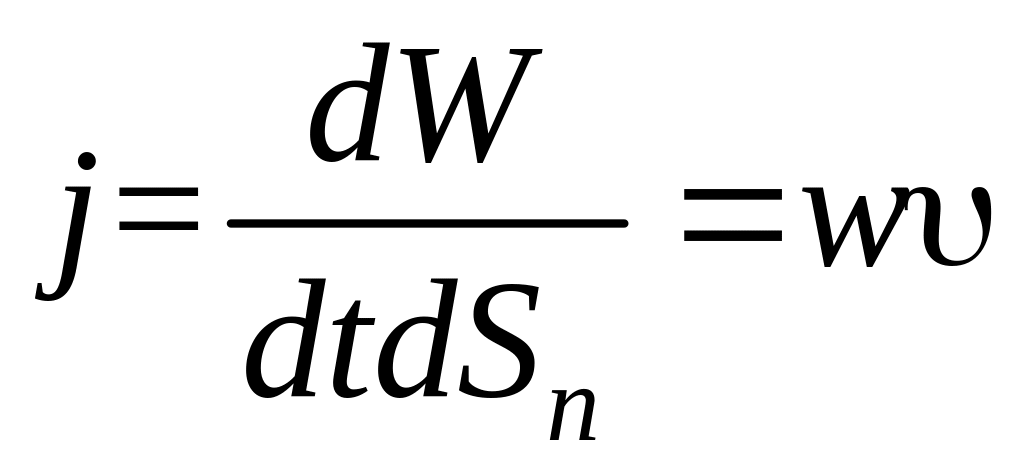, (10.1)

где энергия dW = wdtdS_n равна энергии, переносимой через попереч-

ное сечение параллелепипеда, dS_n, перпендикулярное к направлению распространения волны. Объем данного параллелепипеда равен dtdS_n (см. рис. 10.2).

Направление вектора плотности потока энергии совпадает с направлением скорости распространения волны, т. е.

. (10.2)

Таким образом, вектор плотности потока энергии волны равен произведению вектора скорости распространения энергии волны на величину ее объемной плотности. Вектор называется вектором Умова.

Из формул (10.18) и (10.19) следует, что объемная плотность энергии и плотность потока энергии синусоидальной волны пропор

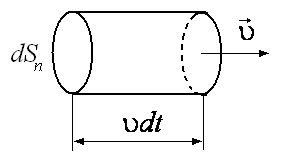
Рис. 10.1

циональны квадрату амплитуды волны и квадрату частоты волны. Формула (10.20) справедлива для плотности потока энергии волн любого типа.

Волновые явления в упругой среде Волновой пакет. Групповая скорость волны

Все реальные волны отличаются от синусоидальных. Оказывается, что любую несинусоидальную волну можно заменить эквивалентной ей системой синусоидальных волн. Описание волны упрощается, если волна мало отличается от синусоидальной - квазисинусоидальная волна.

Квазисинусоидальная волна представляет собой совокупность синусоидальных волн, частоты которых мало отличаются от некоторой основной частоты . Такую несинусоидальную волну называют группой волн, или волновым пакетом.

Дисперсией. называется зависимость свойства среды (например, скорость распространения волны) от частоты

Рассмотрим простейший волновой пакет, образованный двумя плоскими продольными синусоидальными волнами, распространяющимися вдоль оси ОХ. Пусть амплитуды этих волн одинаковы, начальные фазы равны нулю, а частоты и волновые числа несколько различны, но близки друг к другу:

s₁ = A₀ sin(₁ t – k₁ x), s₂ = A₀ sin(₂ t – k₂ x)

Для результирующей волны получим:

s = s₁ + s₂ = 2A₀ cos(t – kx)sin(t – kx),

где:

/

Амплитуда А этой волны постоянной не является, а зависит от координаты х и времени:

A = 2A₀ cos(t – kx).

Выражение для амплитуды волнового пакета также является уравнением плоской синусоидальной волны, которая является волной амплитуды колебаний. Фаза этой волны равна:

Ф_A = t – kx.

Скорость и распространения энергии волнового пакета наз. групповой скоростью, которая равна фазовой скорости волны амплитуды. Дифференцируя выражение для Ф_А и полагая Ф_А = const, получим:

.

В пределе, когда  и Δk стремятся к нулю, получим:

. (10.3)

С учетом того, что , формула (10.1) примет вид:

. (10.4)

Подставив в (10.2) выражение частоты через фазовую скорость  , и выполнив дифференцирование, получим:

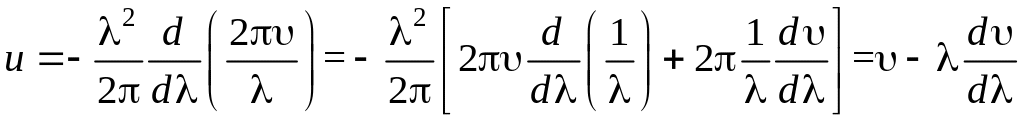. (10.5)

Формула (10.3) устанавливает соотношение между групповой и фазовой скоростью волн, и получила название формулы Рэлея. Скорость и называется групповой скоростью пакета волн. В случае отсутствия дисперсии волн (d/d = 0) групповая скорость волн в пакете совпадает с их фазовой скоростью.

Так как скорость группы волн характеризует распространение амплитуды волнового пакета, то групповая скорость определяет скорость распространения энергии волны.