
- •1 Функция выживания. Кривая смертей.
- •2. Интенсивность смерти. Макрохарактеристики продолжительности жизни.
- •3.Распределение остаточного времени жизни. Основные величины,связанные с остаточным временем жизни.
- •4.Числовые характеристики остаточного времени жизни.Частичная остаточная продолжительность жизни.
- •5.Закон Распределения Вероятностей округленного времени жизни. Числовые характеристики округленного времени жизни.
- •6. Равномерное распределение смертей.
- •7.Постоянная интенсивность смерти.
- •8.Предположение Балдуччи.
- •9.Мат.Ожидание распределения жизни для дробных возрастов.
- •10. Общие таблицы продолжительности жизни. Таблицы отбора риска.
- •11.Таблицы с отбором ограниченного действия.
- •12.Анализ индивидуальных убытков при красткосрочном страховании жизни.
- •13. Точный расчет характеристик суммарного ущерба при краткосрочном страховании жизни.
- •Из курса теории вероятностей известно, что в случае дискретных случайных величин вида:
- •14. Приближенные методы расчета вероятности неразорения.
- •15. Принципы назначения страховых премий
- •1. Вычисление платы за страховку
- •4.4. Распределение пропорционально средним квадратическим отклонениям
- •16. Модели долгосрочного страхования жизни
- •1.2. Страхование с выплатой страхового пособия в конце года смерти
- •17. Принципы назначения нетто-премий. Полное страхование жизни.
- •1. Актуарная стоимость страховой выплаты
- •Для упрощения записи вводят и выражения:
- •18.Расчет нетто-премий при n-летнем чисто накопительном, временном и смешанном непрерывном страховании жизни.
- •19. Расчет нетто-премий при полном страховании жизни с выплатой страхового пособия в конце последнего года жизни.
- •21. Связь между непрерывными и дискретными видами страхования
- •22.Анализ суммарного иска в одной простой модели
- •23. Полная пожизненная рента
- •24. Временная пожизненная рента
- •25. Отсроченная пожизненная рента
- •26. Актуарная современная стоимость и актуарная наращенная сумма
- •27. Пожизненные постоянные р-срочные ренты
- •3.2. Временная пожизненная рента
- •28. Непрерывные пожизненные ренты
- •29. Схема расчета периодических нетто-премий. Периодические нетто премии при полном дискретном страховании жизни.
- •2.1. Полное дискретное страхование жизни
- •30.Периодические нетто-премии при непрерывном страховании жизни.
- •31.Понятие резерва нетто-премий.
- •32.Перспективная формула расчета резерва нетто-премий при полном дискретном страховании жизни.
- •33. Перспективная формула расчета резерва нетто-премий при непрерывном страховании жизни.
- •34.Ретроспективная формула расчета резерва нетто примий при полном дискретном страховании жизни.
- •§ 1. Сущность договоров перестрахования
- •2.2. Пропорциональное эксцедентное перестрахование
- •38.. Сущность договоров перестрахования
1.2. Страхование с выплатой страхового пособия в конце года смерти
Здесь
речь идет о дискретных
аналогах
рассмотренных выше непрерывных видов
страхования, когда выплата пособия
производится в конце года смерти
застрахованного, то есть в момент времени
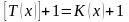 .
Тогда, для:
.
Тогда, для:
а) дискретного
полного страхования жизни: ,
;
,
;
б)
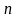 -
летнего дискретного временного
страхования жизни:
,
-
летнего дискретного временного
страхования жизни:
,
 в)
-
летнего дискретного смешанного
страхования жизни:
в)
-
летнего дискретного смешанного
страхования жизни: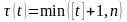 ,
;
г) полного дискретного
страхования жизни, отсроченного на
лет:
,
,
;
г) полного дискретного
страхования жизни, отсроченного на
лет:
,
д) полного страхования жизни с переменной страховой выплатой, например, с ежегодно возрастающим пособием
,
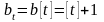 .
.
17. Принципы назначения нетто-премий. Полное страхование жизни.
1. Актуарная стоимость страховой выплаты
Современная стоимость
(на момент заключения договора страхования)
страховой выплаты
будет определяться как ,где
- сложная процентная ставка,
,где
- сложная процентная ставка,
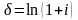 - сила роста (непрерывная процентная
ставка),
- сила роста (непрерывная процентная
ставка),
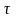 - момент выплаты страховой суммы.
- момент выплаты страховой суммы.
Так как
является случайной величиной, то разовая
нетто-премия равна ее актуарной стоимости,
а именно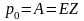 ,
где
,
где .
Для конкретных видов страхования
общая формула (9) может быть упрощена и
конкретизирована, и современная стоимость
.
Для конкретных видов страхования
общая формула (9) может быть упрощена и
конкретизирована, и современная стоимость
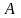 может быть выражена через характеристики
продолжительности жизни, которые были
рассмотрены ранее.
может быть выражена через характеристики
продолжительности жизни, которые были
рассмотрены ранее.
Для обеспечения единого подхода к решению актуарных задач по страхованию жизни в 1898 г. на втором Международном конгрессе актуариев в Лондоне были приняты единые актуарные обозначения. Поэтому для того, чтобы подчеркнуть, что речь идет о конкретных страховых договорах, переменные и снабжаются различными индексами, согласно следующим правилам:
Справа внизу ставится возраст х застрахованного на момент заключения договора:
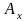 .
.Если договор страхования непрерывный, то есть, страховое пособие выплачивается в момент смерти, то сверху ставится черта:
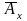 .
.Если договор действует ограниченный период времени n, то после возраста x через двоеточие ставится дополнительный индекс , обрамленный уголком:
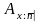 .
.Если договор отсрочен на m лет, то внизу слева ставится индекс
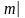 :
:
 .
.Если величина страхового пособия регулярно возрастает, то добавляется буква
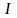 :
:
 .
.Используется также индекс 1 справа сверху. Например,
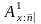 означает,
что первым наступил страховой случай
– смерть застрахованного в момент
времени
означает,
что первым наступил страховой случай
– смерть застрахованного в момент
времени
 ;
а
;
а
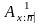 означает, что застрахованный умер не
ранее, чем через n
лет с момента заключения договора
страхования, и страховой случай наступил
в момент времени
означает, что застрахованный умер не
ранее, чем через n
лет с момента заключения договора
страхования, и страховой случай наступил
в момент времени
Перейдем теперь к рассмотрению конкретных видов страхования.
2.2. Полное страхование
жизниСогласно
формулам (1) и (9) получаем
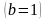 :
:
 ,
и нетто-премия будет равна математическому
ожиданию
,
и нетто-премия будет равна математическому
ожиданию
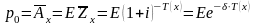 .Обозначив
.Обозначив
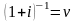 ,
можем получить:
,
можем получить:
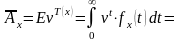
 .А
если ввести обозначение:
.А
если ввести обозначение:
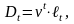
то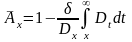 .Функцию
.Функцию
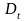 называют замещающей или упрощающей,
используется также и термин –
коммутационная
функция.
называют замещающей или упрощающей,
используется также и термин –
коммутационная
функция.
