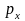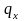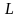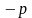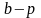9.Мат.Ожидание распределения жизни для дробных возрастов.

задача определения закона распределения для дробных возрастов , решается с помощью интерполяции. Если справедливо предположение о равномерном распределении смертей внутри года, то апроксимируется линейной функцией вида: .Тогда, линейное приближение примет вид , .Если представить х в виде , , то можно записать .

________________________________________________________________________________________

10. Общие таблицы продолжительности жизни. Таблицы отбора риска.

страховые компании должны иметь целый спектр таблиц продолжительности жизни для различных групп населения. Такие таблицы называются таблицами с отбором или таблицами отбора риска (select tables). В них, помимо возраста, учитываются и другие факторы, влияющие на смертность.. Термин «отбор» и означает, что люди попадают в соответствующую таблицу после некоторого отбора.

Смертность среди людей, включенных в такие таблицы, зависит не только от возраста, но и от момента проведения отбора. Ясно, что смертность тех, кто успешно прошел, например, медицинское обслуживание, ниже, чем среди остальных людей. Однако эта зависимость с течением времени практически исчезает. Так, если в возрасте 30-ти лет человек прошел успешный отбор, то это оказывает существенное влияние на вероятность смерти в течение нескольких ближайших лет, но к годам 50-ти вероятность его смерти фактически зависит только от образа жизни индивида в течение последних 10-15 лет.В связи с этим величины, включаемые в таблицы отбора риска, имеют два аргумента: х - момент отбора и - время, прошедшее с момента отбора.

________________________________________________________________________________________

11.Таблицы с отбором ограниченного действия.

Теоретически влияние отбора продолжается неограниченно долго. Однако с течением времени это влияние уменьшается и существует некоторый конечный период времени, начиная с которого можно пренебречь влиянием отбора. Этот период называется периодом действия отбора или сроком селекции и таблица, используемая после истечения срока селекции, называется окончательной таблицей продолжительности жизни, и все характеристики жизни будут рассматриваться уже как функции только от достигнутого возраста. Такие таблицы называются таблицами с отбором ограниченного действия.

________________________________________________________________________________________

12.Анализ индивидуальных убытков при красткосрочном страховании жизни.

Модели страхования жизни делятся на две большие группы: краткосрочное страхование – сроком на один год и долгосрочное – более одного года.

Рассмотрим простейший вид краткосрочного страхования жизни. Человек платит страховой компании 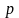рублей (страховая премия), а компания выплачивает наследникам застрахованного 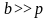рублей в случае смерти человека в течение года, и не платит ничего, если застрахованный не умрет в течение года. Величину 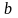называют страховой выплатой. И важнейшей задачей является определение зависимостей между величинами и .

Застрахованный, купив за рублей страховой полис, избавил себя от риска финансовых потерь, связанных с неопределенностью момента смерти. Этот риск приняла на себя страховая компания, и риск заключается в случайности убытка по рассматриваемому договору. Этот индивидуальный убыток является элементарной составляющей финансового риска компании и представляет собой случайную величину 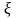с законом распределения

	0

Здесь - вероятность смерти в течение года застрахованного в возрасте х лет; а .

Средняя величина убытка (математическое ожидание) равна ,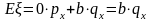

а дисперсия – . наряду с величиной рассмотрим и случайную величину , описывающую потери страховой компании от заключенного договора страхования

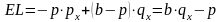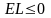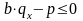Вычислим математическое ожидание потерь компании . Так как средние потери компании должны быть неположительными, то есть , то или . А минимально возможное значение , удовлетворяющее последнему неравенству, равно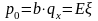 , и называется нетто-премией.Таким образом, нетто-премия соответствует средним нулевым потерям компании.

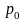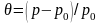На самом деле реальная плата за страховку должна быть больше , так как, во-первых, компания должна учитывать фактор случайности , во-вторых, в сумму входят и различные организационные затраты. Плата должна при этом гарантировать малую вероятность разорения компании. Разница между премией и нетто-премией называется страховой надбавкой (защитная надбавка, надбавка за безопасность), а величина (называется относительной страховой надбавкой. Страховая надбавка необходима для защиты компании от разорения в виду случайности вариаций индивидуальных исков.

Таким образом, общая плата за страховку, без учета организационных затрат, имеет вид:

.

________________________________________________________________________________________
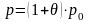