32.Перспективная формула расчета резерва нетто-премий при полном дискретном страховании жизни.

33. Перспективная формула расчета резерва нетто-премий при непрерывном страховании жизни.

34.Ретроспективная формула расчета резерва нетто примий при полном дискретном страховании жизни.

36. Методические рекомендации по расчету страховых резервов

В качестве основных факторов, под влиянием которых формируется система страховых резервов, можно отметить следующие:

Инверсия цикла страховой организации.

Устойчивость страхового портфеля.

Рисковая структура страхового портфеля.

Организационная структура страховой организации.

Вовлеченность страховой организации в инвестиционную деятельность.

Уровень развития перестрахования на рынке.

37

§ 1. Сущность договоров перестрахования

Клиент заключает договор страхования со страховой компанией для того, чтобы избавиться от финансовых потерь, связанных с неопределенностью распределения тех или иных случайных событий. После заключения договора страхования клиент избавился от этого риска за фиксированную (неслучайную) плату (без учета издержек): ..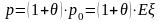

Для решения этой проблемы страховая компания может поступить так же, как и ее клиенты – застраховать свой риск в другой страховой компании. Такой вид страхования называется перестрахованием.

Компания, заключившая договоры непосредственно с клиентом и желающая перестраховать часть своего риска, называется передающей компанией («цедентом»), а компания, которая ее страхует, называется перестраховочной компанией («цессионаром»).

Существуют различные причины, по которым страховые компании вынуждены обращаться к перестрахованию. Например, это недавно созданные компании, финансовое положение которых пока еще неустойчиво из-за недостаточного размера его страхового портфеля, или даже более крупная страховая компания при покрытии страховых рисков «лиц, занимающих ключевые посты» («jumbo risques»), или при обеспечении наследственного права в крупных размерах.

При перестраховании могут перестраховываться как чрезмерно большие частные иски, так и суммарный иск за определенный период. Основное деление договоров перестрахования на различные типы связано с видом разделения ответственности между передающей компанией и перестраховочной компанией. Существуют многочисленные формы перестрахования, которые в техническом плане можно разделить на две категории: договоры пропорционального перестрахования и договоры перестрахования превышения потерь.

Пропорциональным перестрахованием называется такой вид перестрахования, при котором передающая компания самостоятельно оплачивает некоторую долю 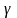от каждого иска 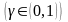, а перестраховочная компания удовлетворяет оставшуюся долю иска . Параметр называется пределом удержания.

Перестрахованием превышения потерь называется такой вид перестрахования, при котором передающая компания самостоятельно оплачивает все иски до некоторого предела 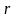руб., а если иск превышает руб., то на остаток суммы предъявляет иск к перестраховочной компании. Параметр также называется пределом удержания. Если это правило применяется к общему иску за некоторый период, то такое перестрахование называется перестрахованием, останавливающим потери, или перестрахованием на базе эксцедента убыточности. Параметр в этом случае называется франшизой или вычитаемой франшизой.

Для перестраховочной компании эта операция выглядит как обычное страхование, поэтому плата за перестрахование риска будет равна , где – ожидаемый иск к перестраховочной компании, – относительная страховая надбавка, установленная перестраховочной компанией. Будем рассматривать договоры перестрахования только с точки зрения предающей компании, поэтому считаем фиксированной величиной. И основная проблема будет заключаться в выборе предела удержания, оптимального с точки зрения передающей компании. Следует отметить, что перестраховочные тарифы также должны базироваться на таблицах отбора риска

2. ПРОПОРЦИОНАЛЬНОЕ ПЕРЕСТРАХОВАНИЕ2.1. Чистое пропорциональное перестрахованиеПри этом виде перестрахования страховщик передает перестраховщику одинаковую долю от всех рисков страхового портфеля, которые он принимает в одной и той же отрасли. То есть перестраховщик покрывает одну и ту же часть исков во всех страховых случаях, оплаченных страховщиком.

Пусть портфель страховой компании состоит из договоров страхования с исками 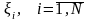. Тогда, при наступлении страхового случая, сумму платит передающая компания, а сумму 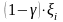выплачивает перестраховочная компанияТаким образом, суммарный иск к страховой компании уменьшается и становится равным .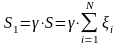

Однако одновременно уменьшается и капитал передающей компании.

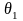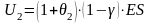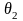До заключения договора перестрахования капитал передающей компании был равен где - относительная страховая надбавка, обеспечивающая страхователю определенную вероятность неразорения . Заключение договора перестрахования приводит к выплате перестраховочной компании суммы , где - относительная страховая надбавка, установленная перестрахователем. Поэтому капитал передающей компании станет равным: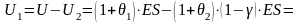 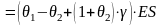. Следовательно, вероятность неразорения передающей компании становится равной ил .При аппроксимации нормальным распределением, получаем:

, где -

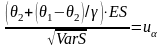квантиль нормального распределения.

Отсюда следует, что для максимизации вероятности неразорения необходимо выбрать параметр таким образом, чтобы максимизировать величину .

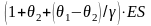Видно, что:

а) Если 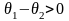, то есть 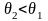, то максимум достигается при . Другими словами, если перестраховочная компания устанавливает меньшую страховую надбавку , то нужно перестраховать все иски. При этом вероятность разорения будет равна нулю. Однако этот случай практического интереса не имеет, так как реально справедливо равенство .

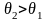б) Если 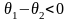, то есть , то 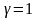. Другими словами, если перестраховочная компания устанавливает большую страховую надбавку, то от перестрахования нужно вообще отказаться.

в) Если 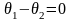, то есть , то вероятность неразорения от не зависит. Другими словами, может принимать все значения в промежутке .

Следовательно, в рамках простейшей модели риска (без учета неоднородности договоров, резервов и различного рода издержек) чистое пропорциональное перестрахование не представляет никакого интереса с точки зрения математики.