1 Функция выживания. Кривая смертей.

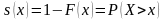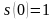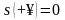В качестве первичной характеристики продолжительности жизни применяют так называемую функцию выживания ,которая определяет вероятность того, что случайная величина X принимает значения, большие x, то есть случайно взятый человек уже прожил, по крайней мере, лет. Исходя из свойств функции распределения вероятностей, можем записать следующие свойства функция выживания:1) ,2) ,3) 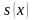- непрерывная и строго убывающая функция. Статистическим аналогом функции выживания s(x) является величина , равная среднему числу лиц, доживших до x лет: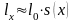 , где l₀ - количество новорожденных человек. Тогда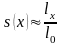 характеризует среднюю долю живых представителей некоторой фиксированной группы новорожденных к моменту времени x. График функци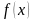и (или 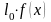) называют кривой смертей. следующие свойства функции f (x):1)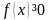 . 2) ,

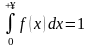3. .

_______________________________________________________________________________________

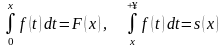2. Интенсивность смерти. Макрохарактеристики продолжительности жизни.

Еще одной характеристикой продолжительности жизни является интенсивность смертности. Это величина, которая характеризует вероятность смерти в интервале 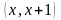человека, дожившего до x лет: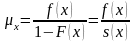 Статистическим аналогом интенсивности смертности , является величина ,характеризующая долю тех представителей исходной группы, доживших до возраста x лет, которые умрут в течение ближайшего года.

Для случайной величины 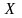определяют и такие числовые характеристики как математическое ожидание 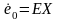и дисперсия 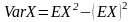, которые можно вычислить по формулам: ,___ 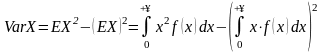общая или упрощенная таблица продолжительности жизни (aggregate tables), которая содержит информацию о статистических свойствах времени жизни случайно выбранного человека, относительно которого известен только его возраст.

В таблицу включены следующие характеристики:

а) 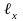- среднее число живых представителей некоторой группы из новорожденных к возрасту x лет;

б) - число представителей группы, умерших в возрасте от x до лет;

в) 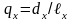- доля тех представителей группы, доживших до возраста x лет, которые умрут в течение ближайшего года;

г) 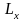- среднее суммарное число лет, прожитых представителями группы в возрасте от x до лет;

д) 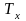- среднее суммарное число лет, прожитых представителями группы в возрасте от x лет и более;

е) 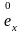- среднее остаточное время жизни.

________________________________________________________________________________________

3.Распределение остаточного времени жизни. Основные величины,связанные с остаточным временем жизни.

При страховании жизни страхователь имеет дело с конкретными людьми, уже дожившими до определенного возраста x. Поэтому необходимо рассмотрение случайной величины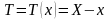 определяющей остаточное время жизни человека, дожившего до х лет.

Закон распределения вероятностей этой случайной величины можно задать как 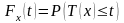. Эту вероятность в страховой математике принято обозначать как 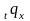: 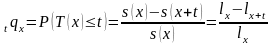-вероятность смерти человека, достигшего возраста x лет, в течение ближайших t лет.

Дополнительная вероятность 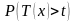обозначается как :

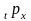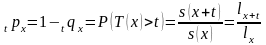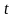-это вероятность того, что человек в возрасте x лет проживет еще не менее лет.

________________________________________________________________________________________