1.2.1. Однотональная модуляция

Простейшая форма модулированного сигнала создается при однотональной амплитудной модуляции – модуляции несущего сигнала гармоническим колебанием с одной частотой  (4):

u(t) = U_н (1+Mcost)cos ₀t.

Значения начальных фазовых углов несущего и модулирующего колебания здесь для упрощения получаемых выражений приняты равными нулю. С учетом формулы:

cos(x) cos(y) = (1/2)[cos(x+y)+cos(x-y)],

из выражения (4) получаем:

u(t) = U_нcos₀t + (U_н M/2)cos[(₀ + ) t] + (U_н M/2)cos[(₀ - ) t]. (5)

Отсюда следует, что модулирующее колебание с частотой  перемещается в область частоты _o и расщепляется на два колебания, симметричные относительно частоты _o, с частотами соответственно (_o+верхняя боковая частота, и (_o-нижняя боковая частота (рис. 6 для сигнала, приведенного на рис. 3).

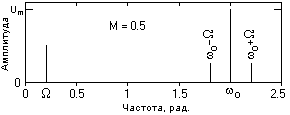
Рис. 6. Физические спектры сигналов

Амплитуды колебаний на боковых частотах равны друг другу, и при 100%-ной модуляции равны половине амплитуды колебаний несущей частоты. Если получить уравнение (5) с учетом начальных фаз несущей и модулирующей частоты, то правило изменения фаз аналогично изменению частоты: начальная фаза модулирующего колебания для верхней боковой частоты складывается с начальной фазой несущей, для нижней – вычитаются из фазы несущей. Физическая ширина спектра модулированного сигнала в два раза больше ширины спектра сигнала модуляции.

1.2.2. Энергия однотонального ам-сигнала

Обозначим раздельными индексами (нес.  несущая, вб.  верхняя боковая, нб.  нижняя боковая) составляющие колебания в левой части выражения (5) однотонального АМ-сигнала и определим функцию его мгновенной мощности:

u(t) = u_нес(t) + u_вб(t) + u_нб(t).

p(t) = u²_нес(t)+u²_вб(t)+u²_нб(t)+2u_нес(t)u_вб(t)+2u_нес(t)u_нб(t)+2u_вб(t)u_нб(t). (6)

Для определения средней мощности сигнала выполним усреднение функции p(t):

P_u = _.

Все взаимные мощности модулированного сигнала при усреднении становятся равными нулю (спектры не перекрываются), при этом:

P_u = Р_нес + Р_вб + Р_нб = U_н²/2/R + (U_нM)² /4/R. (7)

Доля мощности боковых частот в единицах мощности несущей частоты:

(Р_вб + Р_нб)/Р_нес = М²/2, (8)

т.е. не превышает 50% даже при 100%-ной модуляции.

Под полезной мощностью модулированных сигналов понимают мощность боковых частот, несущих информацию.

Коэффициент полезного действия модуляции определяется отношением мощности боковых частот к общей мощности модулированного сигнала:

_АМ = (U_н² M²/4) /P_u = M²/(М²+2). (9)

Как можно видеть на рис. 7, даже при М =1 КПД амплитудной модуляции составляет только 33%, а при практическом использовании обычно меньше 20%.

Рис. 7. КПД амплитудной модуляции

Для модулированных сигналов применяют также понятие пиковой мощности P_max. Значение пиковой мощности для однотонального АМ-сигнала:

P_max = U_н² (1+M)².

1.2.3. Многотональный модулирующий сигнал

Многотональный модулирующий сигнал имеет произвольный спектральный состав. Математическая модель такого сигнала может быть аппроксимирована тригонометрической суммой гармонических составляющих, в пределе бесконечной:

е(t,n) = a_n cos(_n t + _n), (10)

где значения амплитуд a_n и начальных фаз _n упорядоченной возрастающей последовательности гармоник _n произвольны. Подставляя (10) в (2) и заменяя произведения M·a_n парциальными (частичными) коэффициентами модуляции:

M_n = M·a_n,

получим обобщенное уравнение амплитудно-модулированного сигнала и его физического спектра:

u(t) = U_н[1+ М_ncos(_nt+_n)]cos_ot. (11)

u(t)=U_нcos_ot+(U_н/2) M_ncos[(_o+ _n) t_n]+(U_н/2) M_ncos[(_o - _n)t_n].

На рис. 8 приведен схематический пример амплитудных спектров модулирующего и АМ-сигналов при многотональной модуляции.

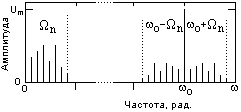
Рис. 8. Многотональная модуляция

Он также содержит полосы верхних и нижних боковых частот относительно несущей частоты _o, являющихся прямой и зеркальной масштабными копиями модулирующего сигнала. Полная ширина спектра АМ-сигнала равна удвоенной ширине спектра модулирующего сигнала.