Измерение «неэнергетических» величин

Из правила (см. выше) следует, что «неэнергетические» величины должны быть преобразованы в энергетические. Так, согласно закону Джоуля-Ленца     P = U²/R     или     P = I² R. Следовательно,     ,     где R₁ — сопротивление, на котором определяется изменяемое напряжение U₁, а R₀ — сопротивление, на котором было определено опорное напряжение U₀.

В общем случае напряжения U₁ и U₀ могут регистрироваться на различных по величине сопротивлениях (R₁ не равно R₀). Такое может быть, например, при определении коэффициента усиления усилителя, имеющего различные выходное и входное сопротивления, или при измерении потерь в согласующем устройстве, трансформирующем сопротивления. Поэтому в общем случае

величина в децибелах = .

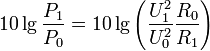Только в частном (весьма распространенном) случае, если оба напряжения U₁ и U₀ измерялись на одном и том же сопротивлении (R₁ = R₀), можно пользоваться кратким выражением   

величина в децибелах = .

4.4 Децибелы «по мощности», «по напряжению» и «по току»

Из приведенных выше рассуждений следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R₁ = R₀ (в частности, если R₁ и R₀ — одно и то же сопротивление, или в случае, если соотношение сопротивлений R₁ и R₀ по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:

дБ по напряжению = ;

дБ по току = .

Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует четко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R₁ не равно R₀, следует пользоваться выражением для общего случая (см. выше).

Нетрудно подсчитать, что, в частности:

• при регистрации мощности изменению на +1 дБ (+1 дБ «по мощности») соответствует приращение мощности в ≈1.259 раза, изменению на −3.01 дБ — снижение мощности в два раза, в то время как

• при регистрации напряжения (силы тока) изменению на +1 дБ (+1 дБ «по напряжению», «по току») будет соответствовать приращение напряжения (силы тока) в ≈1.122 раза, при изменении на −3.01 дБ напряжение (сила тока) снизятся и составят ≈ 0.707 от своего исходного значения.

4.5 Примеры вычислений Переход к дБ

Пусть значение мощности P₁ стало в 2 раза больше исходного значения мощности P₀, тогда

10 lg(P₁/P₀) = 10 lg(2) ≈3.0103 дБ ≈ 3 дБ,

то есть рост мощности на 3 дБ означает её увеличение в 2 раза.

Пусть значение мощности P₁ стало в 2 раза меньше исходного значения мощности P₀, то есть P₁ = 0.5 P₀. Тогда

10 lg(P₁/P₀) = 10 lg(0.5) ≈ −3 дБ,

то есть снижение мощности на 3 дБ означает её снижение в 2 раза. По аналогии:

• рост мощности в 10 раз: 10 lg(P₁/P₀) = 10 lg(10) = 10 дБ, снижение в 10 раз: 10 lg(P₁/P₀) = 10 lg(0.1) = −10 дБ;

• рост в 1 млн раз: 10 lg(P₁/P₀) = 10 lg(1 000 000) = 60 дБ, снижение в 1 млн раз: 10 lg(P₁/P₀) = 10 lg(0.000001) = −60 дБ.

Переход от дБ к «разам»

Чтобы вычислить изменение «в разах» по известному изменению в дБ («dB» в формулах ниже), нужно:

• для мощности: ;

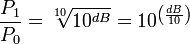• для напряжения (силы тока): .

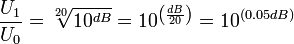Переход от дБ к мощности

Для этого нужно знать значение опорного уровня мощности P₀. Например, при P₀ = 1 мВт и известном изменении на +20 дБ:

Вт.

Переход от дБ к напряжению (току)

Для этого нужно знать значение опорного уровня напряжения U₀ и определиться, регистрировалось ли напряжение на одинаковом сопротивлении, или же для решаемой задачи различие значений сопротивлений не важно. Например, при условии R₀ = R₁, заданном U₀ = 2 В и приросте напряжения на 6 дБ:

≈ 4 В.

Рекомендации

При некотором навыке операции с децибелами вполне реально выполнять в уме. Более того, нередко это очень удобно: вместо умножения, деления, возведения в степень и извлечения корня удается обходиться сложением и вычитанием «децибельных» единиц.

Для этого полезно помнить и научиться применять несложную таблицу:

1 дБ — в 1.25 раза,

3 дБ — в 2 раза,

10 дБ — в 10 раз.

Отсюда, раскладывая «более сложные значения» на «составные», получаем:

6 дБ = 3 дБ + 3 дБ — в 2·2 = в 4 раза,

9 дБ = 3 дБ + 3 дБ + 3 дБ — в 2·2·2 = в 8 раз,

12 дБ = 4 · (3 дБ) — в 2⁴ = в 16 раз

и т. п., а также:

13 дБ = 10 дБ + 3 дБ — в 10·2 = в 20 раз,

20 дБ = 10 дБ + 10 дБ — в 10·10 = в 100 раз,

30 дБ = 3 · (10 дБ) — в 10³ = в 1000 раз

и т. п.

Сложению (вычитанию) значений в дБ соответствует умножение (деление) самих отношений. Отрицательные значения дБ соответствуют обратным отношениям. Например:

• уменьшение мощности в 40 раз — это в 4·10 раз или на −(6 дБ + 10 дБ) = −16 дБ;

• увеличение мощности в 128 раз это 2⁷ или на 7·(3 дБ) = 21 дБ;

• снижение напряжения в 4 раза эквивалентно снижению мощности (величины второго порядка) в 4² = 16 раз; и то и другое при R₁ = R₀ эквивалентно снижению на 4·(−3 дБ) = −12 дБ.