2 . График (рис. 5)

Для интерпретации распределения результатов выполнения теста часто отдается предпочтение гистограмме, поскольку это наиболее подходяще для визуального восприятия, к тому же гистограмма достаточно удобна для визуального сравнения эмпирического распределения с теоретическим нормальным распределением (рис. 5).

3. Меры центральной тенденции

Меры центральной тенденции предназначены для выявления «центрального положения», вокруг которого в основном группируется множество значений данного распределения данных.

М ода – это такое значение, которое встречается наиболее часто среди результатов выполнения теста. Например, для графика № 1 мода равна….

Конечно, не всякое распределение имеет одну моду.

График № 2 имеет две моды, и соответствующее распределение называется бимодальным. Один из наиболее важных выводов в случае бимодального распределения – корректировка трудности заданий теста. По-видимому, в тесте недостаточно представлены задания средней трудности. В том случае, когда все значения баллов учеников встречаются одинаково часто, принято считать, что моды у распределения нет. Рис. 6

Среднее выборочное – среднее арифметическое. Определяется суммированием всех значений совокупности и последующим делением на их число. (Вспомнить понятия наблюдаемого (индивидуального) и истинного балла). Для совокупности индивидуальных баллов х₁, х₂, …, х_N группы N испытуемых среднее значение будет равно:

Среднее арифметическое индивидуальных баллов испытуемых для нашего примера матрицы будет…

Интерпретация мер центральной тенденции.

Генеральная совокупность – множество всех испытуемых, репрезентативная (представительная) – определенная часть испытуемых. Современная теория тестов не работает на маленьких выборках (для IRT выборка должна быть не менее 1000 человек).

Меры центральной тенденции в определенной степени помогают при оценке качества теста в том случае, когда она проводится на репрезентативной выборке учеников. Хороший нормативно-ориентированный тест обеспечивает нормальное распределение индивидуальных баллов учеников, когда среднее значение баллов совпадает с модой и находится в центре распределения, около 68% концентрируются вокруг среднего по нормальному закону, а остальные сходят на нет к краям распределения:

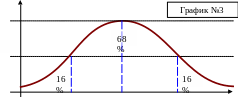
Рис. 7

Нормальное распределение унимодально и симметрично, мода и среднее значение равны.

На малых выборках любые показатели теряют свою стабильность!

Смещение среднего значения влево или вправо говорит о слишком трудной или слишком легкой подборке заданий теста (графики №4, №5).

4. Меры изменчивости.

Размах – измеряет на шкале расстояние, в пределах которого изменяются все значения показателя в распределении. Из индивидуального балла самого сильного ученика вычитают индивидуальный балл самого слабого. В нашем примере размах равен….

Дисперсия. Подсчет дисперсии основан на вычислении отклонений каждого значения показателя от среднего арифметического в распределении: (i=1,2,…,N). Знак отклонения указывает место результата ученика по отношению к среднему арифметическому по тесту. Для ученика с индивидуальным баллом выше среднего значение разности будет положительно, а для тех, у кого результат ниже среднего арифметического, отклонение меньше нуля.

Рис. 8

Рис. 9

Мера изменчивости, называемая дисперсией обозначается и вычисляется по формуле:

. Иногда используют другие формулы для вычисления дисперсии, но они получены из этой путем математических преобразований.

Стандартное отклонение

Стандартное отклонение равно корню квадратному из дисперсии:

Интерпретация. Эти показатели играет важную роль в оценке качества нормативно-ориентированных тестов. Низкая дисперсия индивидуальных баллов говорит о слабой дифференциации испытуемых по уровню подготовленности в группе, что противоречит основной цели нормативно-ориентированных тестов. Излишне высокая дисперсия приводит к искажению вида распределения. Зачастую в оценке характера распределения руководствуются простым соотношением. Для этого величину среднего выборочного сравнивают с утроенным стандартным отклонением. Если , то дисперсия оптимально высока, и можно принять гипотезу о нормальности распределения.