Висновок
Дана курсова робота присвячена симетрії в алгебрі, зокрема, застосуванню симетричних многочленів. В даній роботі було розглянуто: загальні поняття про симетричні многочлени, їх основні властивості, основна теорема теорії симетричних многочленів та застосування симетричних многочленів до розв’язуванні рівнянь, систем рівнянь,, доведення тотожностей, звільнення від ірраціональності у дробах тощо.
У
курсовій роботі було розглянуто способи
розв’язувань систем рівнянь і приклади
їх розв’язання; було виражено степеневі
суми
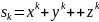через
при
умові
(результати
наведені в таблиці 2.2), введено означення
орбіт O(
),
виражено
орбіти O(
)
через
, (результати
наведені в таблиці 2.2); були розглянуті
випадки, коли для звільнення від
ірраціональностей необхідно застосовувати
симетричні многочлени; було розглянуто
спосіб побудови послідовних наближень,
пов'язаний з симетричними многочленами.
Кожен
параграф проілюстровано прикладами.
Список використаної літератури
1. Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. – М.: МЦНМО, 2002.-240 с.
2. Вейл Г. ,Симметрия.-М.: Наука, 1968.-192 с.
3. Віленкін Н. Я., Метод послідовних наближень. - М.: Физматгіз. - 1961.-203с.
4. Винберг Э. Б. Симметрия многочленов. – М.: МЦНМО, 2001.-24 с.
5. Завало С.Т. та ін. Алгебра і теорія чисел: Практикум. Частина 2. - К.: Вища шк., 1986. - 264с.
6. Кудряшов Н. А. Симетрия алгебраических и дифференциальных уравнений. Соросовский образовательный журнал, №9, 1998, с. 104-110.