
- •1. Постановка задания
- •2. Исходные данные для расчета задания №2
- •3. Решение
- •3.1. Указание сеточной области для рассматриваемой задачи
- •3.2. Построение разностного шаблона для разностной схемы
- •3.3. Оценка погрешности аппроксимации разностной схемы
- •3.4. Сравнение числа итераций с теоретическими оценками
- •3.5. Программная реализация разностной схемы
3.3. Оценка погрешности аппроксимации разностной схемы
Перепишем систему сеточных уравнений в виде:
![]() (5)
(5)
Отметим,
что каждое из уравнений системы (5)
содержит лишь пять неизвестных um+1,n,
um-1,n
,
um,n+1,
um,n-1
, um,n
хотя
в полной системе разностных уравнений
таких неизвестных величин {um,n}
составляет
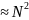 .
Таким образом, матрица системы (5) является
сильно разреженной.
.
Таким образом, матрица системы (5) является
сильно разреженной.
Задача на собственные значения для оператора А состоит в том, чтобы найти числа λ (собственные числа или собственные значения) такие, для которых уравнение Аy= λу имеет нетривиальные решения (собственные функции), а также найти сами собственные функции у.
Числом
обусловленности линейного оператора
А, дествующего в нормированном пространстве
Rm,
а
также числом обусловленности системы
линейных уравнений Ax=f
назовем
величину μ(А) =
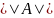 *
*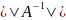 .
Таким
.
Таким
образом появляется связь числа обусловленности с выбором нормы.
Предположим, что матрица и правая часть системы Ax=f заданы не точно. При этом погрешность матрицы составляет δА, а правой части δf. Можно показать, что для погрешности δх имеет следующая оценка:
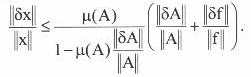
В
частности, если δА
=0, то

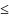 μ(А)
μ(А)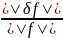 .
При этом решение уравнения Ax=f
и
его погрешность δх не при всех f
одинаково
чувствительно к возмущениям δ
f,
а существенно зависит от числа
обусловленности μ(А)
.
При этом решение уравнения Ax=f
и
его погрешность δх не при всех f
одинаково
чувствительно к возмущениям δ
f,
а существенно зависит от числа
обусловленности μ(А)
линейного
оператора А. При этом μ(А)
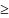
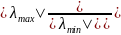 , где
, где
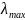 (А),
(А),
 (А)
- соответственно наибольшее и наименьшее
по модулю собственные числа матрицы
А. Матрицы с большим числом обусловленности
(ориентировочно μ(А)>103)
называются плохо обусловленными. При
численном решении систем с плохо
обусловленными матрицами возможно
сильное накопление по1решностей,
что следует из оценки погрешности δх.
Имеет место следующая оценка для
собственных значений задачи Lhuh
= Fh:
(А)
- соответственно наибольшее и наименьшее
по модулю собственные числа матрицы
А. Матрицы с большим числом обусловленности
(ориентировочно μ(А)>103)
называются плохо обусловленными. При
численном решении систем с плохо
обусловленными матрицами возможно
сильное накопление по1решностей,
что следует из оценки погрешности δх.
Имеет место следующая оценка для
собственных значений задачи Lhuh
= Fh:
(Lh) (Lh),
где (Lh) и (Lh) - соответственно наибольшее и наименьшее по
модулю собственные числа матрицы Lh:
(Lh)
=
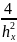
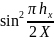 +
+
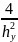
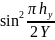 =
=
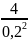
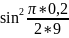 +
+
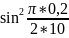 = 0,2204
= 0,2204
(Lh)
=
 +
+
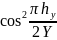 =
=
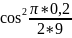 +
+
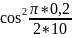 = 199,78
= 199,78
μ(Lh)
=
=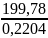 = 906,4
= 906,4
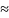 103
103
3.4. Сравнение числа итераций с теоретическими оценками
Итерационный процесс Зейделя:
![]() (6)
(6)
Слагаемые с индексами (m-l,n) и (m,n-l) берутся с k-ой итерации, т.е. в вычислениях используются уточненные значения функции в этих точках. Расчет по формуле (6) при движении, например, слева направо от границы области позволяет последовательно вычислить значения функции на слоях
y = const (или х = const). Использование уточненных значений функции улучшает сходимость метода итераций и позволяет уменьшить требуемый для реализации метода объем оперативной памяти ЭВМ, т.к. в методе Зейделя не требуется одновременно хранить значение функции в каждой точке на двух итерациях.
Теоретическая оценка числа итераций, необходимых для достижения заданной точности при использовании метода Зейделя:
0,1 ln
ln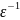 =
0,1
=
0,1 ln
ln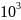 =3 801 832,
=3 801 832,
где N = 46*51 = 2346 – число узлов.
В программной реализации было получено, что заданная точность достигается после 2745 итераций, что значительно меньше теоретической оценки.
