1. Постановка задания

В задании №2 нас будет интересовать уравнение двумерной стацио­нарной теплопроводности в изотропном материале с источниками теплоты 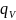: 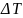= 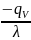. Это простейшее уравнение в частных производных эллиптического типа носит название уравнения Пуассона и записывается в декартовои системе координат следующим образом: = + 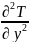= φ(x,y) , где φ(x,y) = .

Пусть задана некоторая область G на плоскости XY, внутри которой определено уравнение Пуассона:

= + = φ(x,y). (1)

На границе Г области G поставлено краевое условие вида:

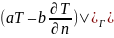= ψ(s) , (2)

где 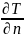- производная в направлении внутренней нормали, , 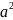+ 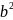= 1 – некоторые числа, s – длина дуги, отсчитываемая вдоль границы Г. Функции φ и ψ считаются заданными. Требуется найти конечное, непрерывное и однозначное численное решение краевой задачи (1), (2) для случая 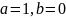- первой краевой задачи или задачи Дирихле.

2. Исходные данные для расчета задания №2

В задании №2 требуется на сетке (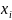 , 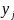) для постоянных шагов по пространственной координате построить разностную схему второго (по пространству) порядка аппроксимации краевой задачи Дирихле для урав­нения Пуассона и произвести численное решение полученной системы уравнений. При этом считать, что , область G есть прямоугольная область G={[0<x<X]x[0<y<Y]} на плоскости XY функции φ и ψ опреде­лены следующим образом φ(x,y) = -2С{х(Х-х) + у(У-у)}, X =9, Y = 10, C = 7; ψ (s)=0.

При выполнении задания №2 необходимо:

• указать сеточную область для рассматриваемой задачи;

• построить разностный шаблон для разностной схемы;

• оценить погрешность аппроксимации разностной схемы;

• используя для решения системы сеточных уравнений, итерационный метод Зейделя, определить число итераций необходимых для достижения заданной точности ε = 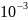и сравнить их теоретическими оцен­ками;

• осуществить программную реализацию разностной схемы, произвести численный расчет и выдать в виде графической зависимости распределение температуры по координатам х и у.

Шаг разностной сетки в направлениях x, y: h = 0,2.

3. Решение

3.1. Указание сеточной области для рассматриваемой задачи

Рассмотрим этапы реализации метода сеток задачи Дирихле для классического уравнения эллиптического типа - уравнения Пуассона:

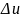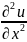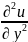= + = φ(x,y), для 0 x X , 0 y Y (3)

с граничным условием: = 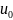(x , y), (4)

где Г - граница области G (рис. 1), в которой ищется конечное, непрерыв­ное и однозначное решение u(х,у) удовлетворяющее уравнению (3) и гра­ничному условию (4).

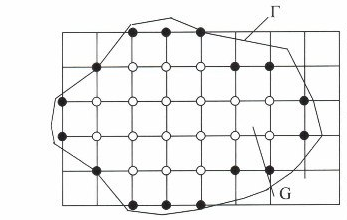
Рис.1

В операторной форме задачу (3),( 4) можно представить следую­щим образом:

Lu = F,

где

Lu =

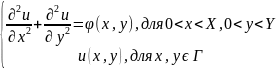
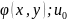и F(x,y) = { (x , y)}.

На первом этапе метода се­ток область G непрерывного из­менения аргументов (х,у) с грани­цей Г заменяют приближающей её сеточной областью 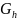с границей 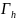. Для этого проведем линии x=const и y=const, так что x=mh_x (m = 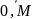) и y=nh_y (n = 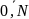). Ве­личины h_x, h_y, называемые шагами разностной сетки, в общем случае могут быть различными.

Точки пересечения линий x=const и y=const называют узлами разно­стной сетки. Различают два типа узлов - внутренние и внешние. Внутрен­ними называют такие узлы, для которых четыре соседних узла (по два в каждом направлении) принадлежат области 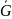= G + Г. Сеточной функцией приписываются нижние индексы. На рис.1 внутренние узлы обозначены пустыми кружочками, а граничные - залитыми.

Совокупность точек (x_m,y_n)=(mh_x,nh_y), попавших внутрь области G или на его границу обозначим через G_h. Точки G_h, лежащие строго внутри области G обозначим 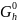(внутренние узлы). Точки G_h, лежащие на грани­це Г области G, будем считать граничными точками сеточной области G_h (внешние узлы). Эту совокупность граничных точек обозначим Г_h.