Используя величину удельной поверхности контакта фаз вначале можно определить рабочий объем аппарата:

а затем его высоту:

(1.59)

Проблема состоит в определении .

При плёночном течении жидкости по стенкам цилиндрического аппарата и контакте её с газовым потоком имеем:

(1.60)

Для насадочного аппарата величину можно выразить через удельную поверхность насадки и долю активной поверхности :

(1.61)

Величина может быть и больше единицы за счёт образования волн на поверхности плёнки и брызг жидкости при высоких скоростях газового потока.

Таким образом, проектный расчёт аппарата с непрерывным контактом фаз в первом приближении завершён, D и Н найдены. Остаётся вопрос, оптимальны ли размеры аппарата?

Критерием оптимальности могут служить затраты на проведение процесса. При заданных характеристиках первой фазы ( , , ), затраты на проведение абсорбции и экстракции можно представить в виде трёх слагаемых V, Δp, .

В качестве первого параметра оптимизации берём расход второй фазы : рост приводит к росту и Ку и к уменьшению V. Однако растёт Δр на прокачку фазы .

В качестве второго параметра оптимизации возьмём фиктивную скорость . При увеличении уменьшается D, возрастает и , что приводит к уменьшению V, но растёт Δр аппарата.

Варьирование значениями параметров оптимизации позволяет спроектировать аппарат, обеспечивающий минимальные затраты на проведение процесса.

1.7.2 Технологический расчет аппарата со ступенчатым контактом фаз.

Особенность процесса – существенная дискретная неоднородность удельной поверхности контакта фаз по высоте аппарата. Кроме того, в большинстве случаев для них не приемлемо допущение о параллельном движении фаз в режиме идеального вытеснения, которое использовалось при выводе основного уравнения массопередачи.

Рассмотрим схему проектного технологического расчёта массообменного аппарата со ступенчатым контактом фаз на примере тарельчатой колонны с противоточным движением газовой и жидкой фаз (рис.1.10).

Расход жидкой фазы , его конечная концентрация, диаметр аппарата и скорости движения фаз и определяется также, как и для аппарата с непрерывным контактом фаз.

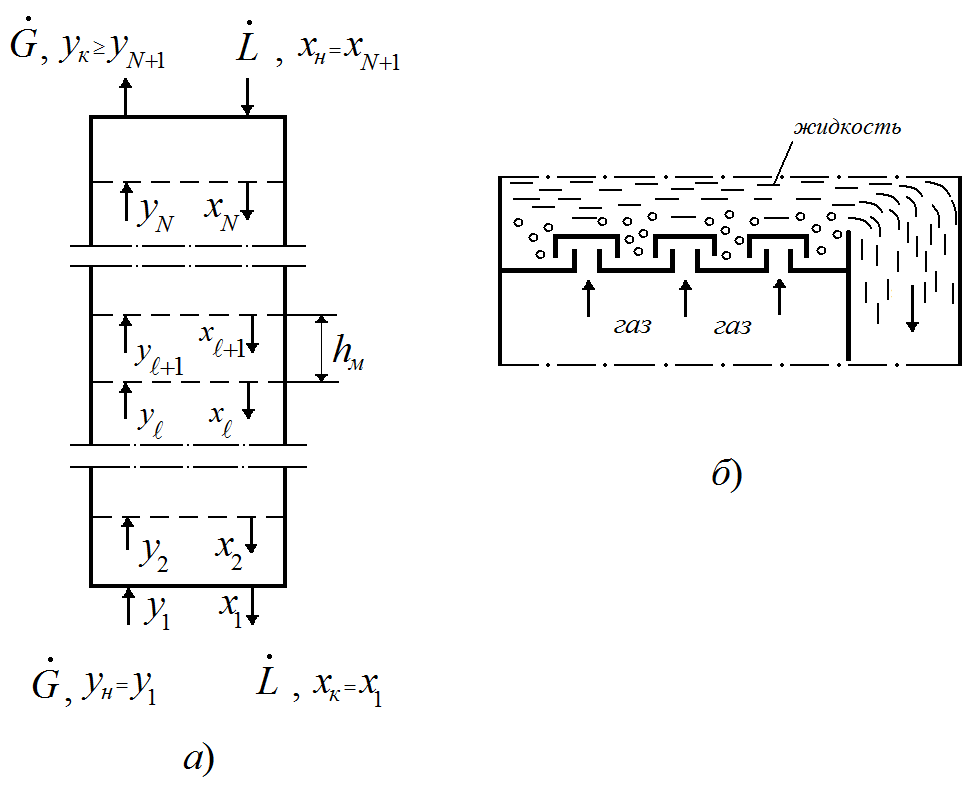
Рис. 1.10. Изменение концентраций фаз по высоте тарельчатой колонны (а) и схема тарельки (б)

Высоту колонны можно связать с числом тарелок N и межтарельчатым расстоянием :

(1.62)

Величина , являясь одним из параметров оптимизации, в первом приближении может определяться из условия максимально допустимого уноса капель газовым потоком. Для различных типов тарелок имеются соотношения связывающие величину уноса е с и скоростью газовой фазы .Обычно допускают 0,1 кг жидкости на 1 кг газа.

Основная задача – определение N, обеспечивающих необходимый перенос распределяемого компонента из одной фазы в другую. Для этого вводится понятие эффективности тарелки по Мэрфри (кпд тарелки) , характеризующее степень достижения равновесия между уходящими с тарелки фазами:

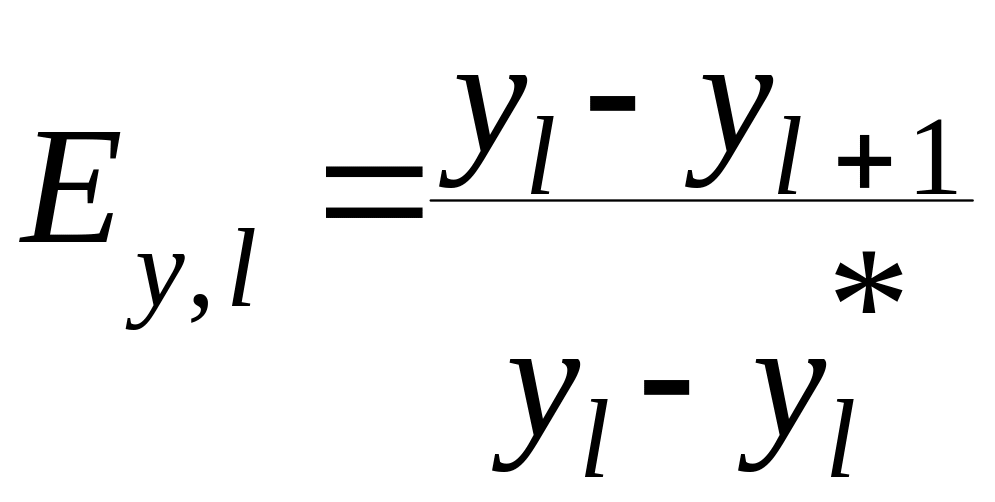(1.63)

где - концентрация распределяемого компонента в газовой фазе, равновесная с уходящим с l-ой тарелки потоком жидкости. Аналогичным образом можно найти , используя концентрации жидкой фазы.

Если , то такую тарелку называют теоретической. Т.е. имеем такой объём аппарата, концентрация распределяемого вещества на выходе из которого равна равновесной концентрации на входе в него: . В этом объёме аппарата происходит процесс полного (теоретического) обмена распределяемого вещества между обеими фазами.

Следует отметить, что при этом составы фаз рассматриваются в различных сечениях аппарата ( - над l-ой тарелкой, - под ней). Таким образом, в любом поперечном сечении аппарата равновесие не достигается , иначе отсутствовала бы движущая сила массопередачи.

Рассмотрим различные способы определения число тарелок N.

Потарелочный расчёт колонны.

Это аналитический метод определения N основан на решение уравнений материального баланса, равновесия и использования эффективности по Мэрфи для каждой тарелки.

Для нижней тарелки под номером 1составы фаз известны .

Рассмотрим вторую тарелку. Запишем необходимые уравнения:

уравнение равновесия , (1.64)

уравнение Мэрфри , (1.65)

уравнение рабочей линии , (1.66)

Итак нашли составы фаз для тарелки 2. Далее, также для 3 тарелки и т.д.

Для тарелки имеем:

(1.67)

(1.68)

(1.69)

Расчёт заканчивается при значении l, для которого начинает выполняться условие , при этом число тарелок N=l. Поскольку число тарелок в аппарате может достигать сотни и более, данный алгоритм необходимо реализовать на компьютере.

Для ориентировочных расчётов, выполняемых вручную, используют упрощенные графические способы нахождения числа тарелок.

Определение числа тарелок с помощью кинетической кривой.

Эффективность по Мэрфри рассчитывается не для каждой тарелки, а лишь для нескольких сечений колонны, аналитическое решение уравнений (1.64-1.69) заменяется графическим.

Алгоритм действий следующий:

— строятся рабочая и равновесная линии;

— для нескольких сечений аппарата (нескольких рабочих концентраций ; ; ) рассчитываются эффективности по Мерфри

—находят величины.

(1.70)

— на диаграмме х – у наносятся точки и т.д. Соединяя их получим кинетическую кривую.

— из точки спускаемся по лестнице до тех пор, пока для точки не выполнится условие . На этом построение заканчивается, необходимое число тарелок в колонне .

Таким образом, аналитическое решение заменяется графическим определением число ступеней лестницы.

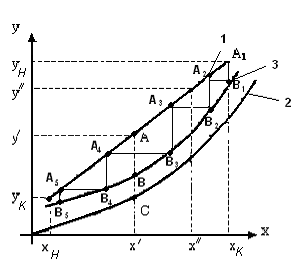
Рис.1.11. Определение числа тарелок с помощью кинетической кривой:

1 – рабочая линия, 2 – равновесная линия, 3 – кинетическая кривая.

Определение числа тарелок с помощью кпд колонны

Кпд колонны:

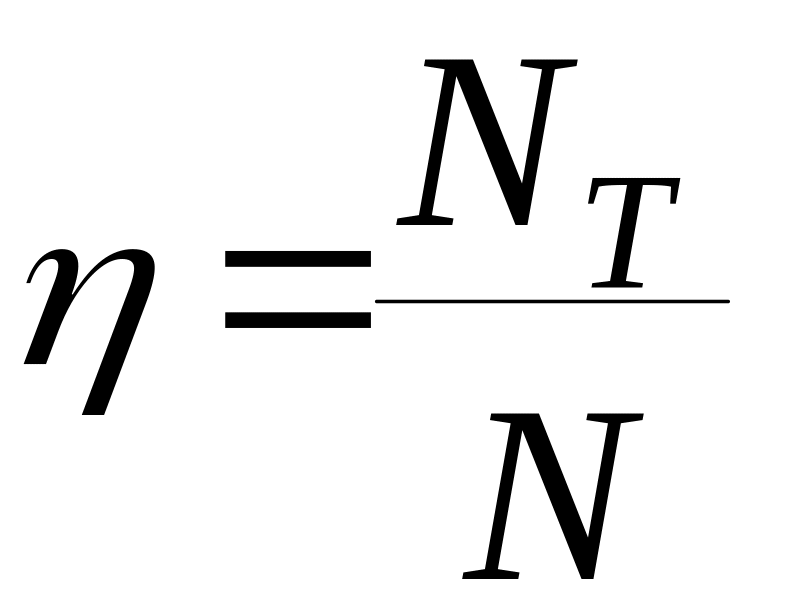(1.71)

где - теоретическое число тарелок, N – действительное число тарелок. Величина находится из опыта. Найти опытным путём достаточно сложно. Необходимы данные по идентичной колонне.

Алгоритм действий следующий:

• аналитическим или графическим способом определяется .

• по известным эмпирическим формулам рассчитывается к.п.д. колонны .

• по формуле (1.71) находят необходимое .