1.6 Упрощенные модели массоотдачи.

Коэффициент массоотдачи характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффициент массоотдачи зависит от многих факторов: физических свойств фазы, скорости потока, определяющих геометрических радиусов и т.д. Определение β требует совместного решения уравнений движения, неразрывности и конвективной диффузии. Это можно сделать для простейшего случая, когда известна поверхность контакта фаз и режим ламинарный. Например, вблизи границы раздела фаз коэффициент массоотдачи для бинарной смеси можно определить по формуле:

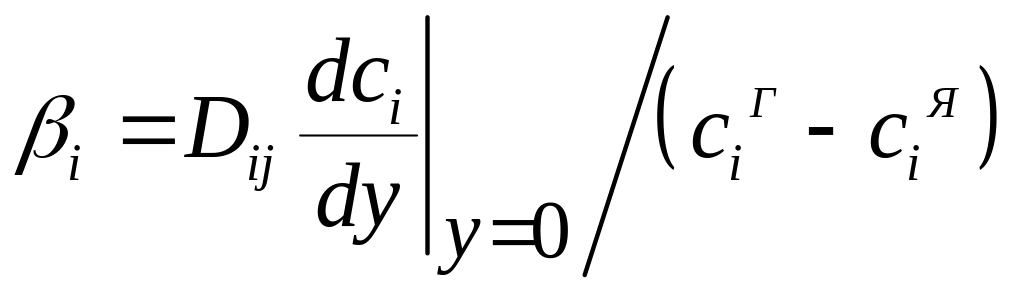
Определение этого коэффициента может быть выполнено экспериментально

Поэтому для определения β иногда пользуются упрощёнными моделями.

Плёночная модель (Нернст, Льюис, Уитмен)

Предполагается, что вблизи межфазной поверхности располагается тонкая неподвижная или ламинарно движущаяся плёнка толщиной , в которой сосредоточено всё сопротивление массоотдачи. Таким образом, эта плёнка представляет собой диффузионный пограничный слой. Предполагается также постоянство диффузионного потока поперек слоя. Тогда имеем:

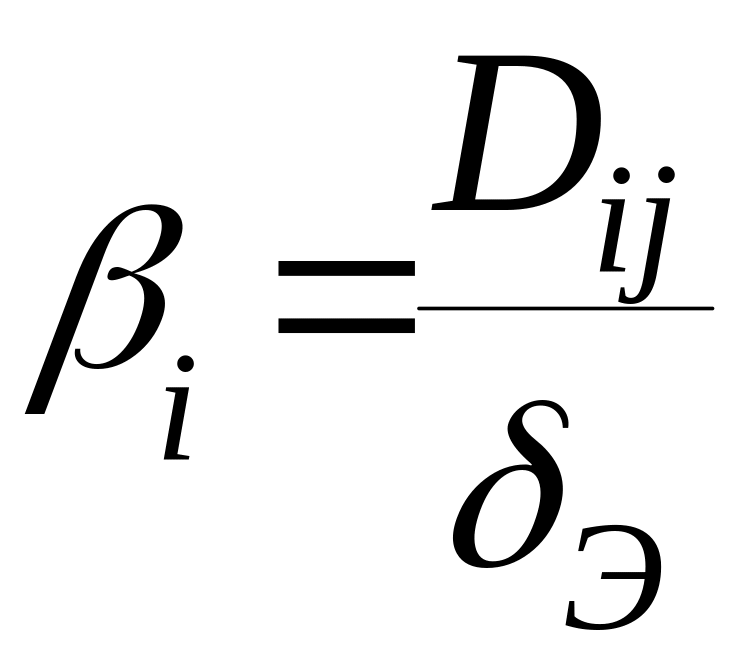(1.53)

Параметром модели является , которая в рамках самой модели не определяется, что является недостатком модели. Кроме того, - (прямая пропорциональность), что не подтверждается на практике. Данная модель пригодна лишь для качественного анализа.

Модель турбулентного диффузионного пограничного слоя

Ландау – Левича

Модель применима для больших значений диффузионного критерия Прандтля , т.е. для жидкостей.

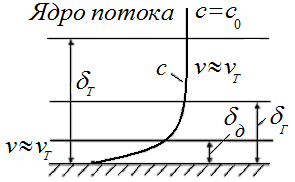
Рис.1.8. Схема турбулентного диффузионного пограничного слоя

Предполагается, что в ядре потока концентрация вещества постоянна, в пределах (турбулентный погранслой) концентрация снижается, в вязком подслое концентрация уменьшается очень быстро, в пределах диффузионного подслоя молекулярный перенос становится основным.

Для систем жидкость – твёрдое тело m=3, для систем г-ж, ж-ж m=2.

Получено для m=3: 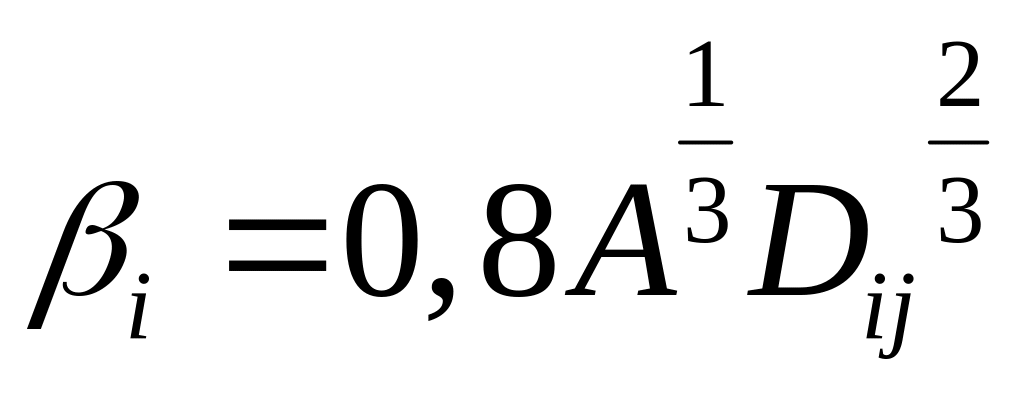, m=2: , (1.54)

где

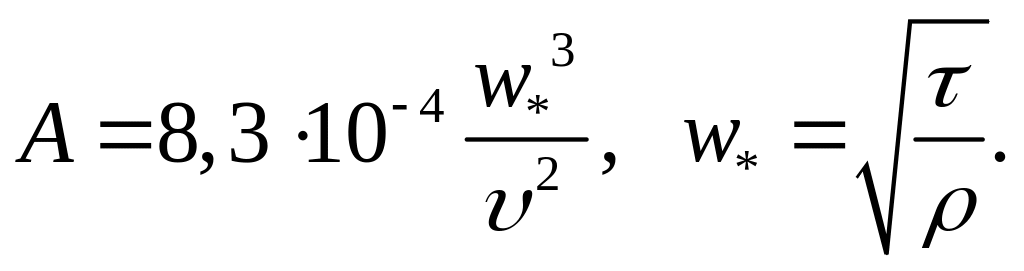
Модель обычно используется для описания массоотдачи в жидкой фазе.

Модель обновления (Хигби).

Предполагается нестационарный молекулярный массоперенос в слой неограниченной толщины, неподвижный относительно границы раздела фаз.

Модель обновления поверхности фазового контакта часто называют моделью проницания. По модели предполагается, что турбулентные пульсации постоянно подводят к поверхности раздела фаз свежую жидкость и смывают порции жидкости, уже прореагировавшей с газом (паром), т.е. каждый элемент поверхности жидкости взаимодействует с газом (паром) в течение некоторого времени t, после чего данный элемент обновляется. Предполагается, что t=const для всех элементов поверхности. Формула Хигби:

(1.55)

Кишиневский, как и Хигби принимает время контакта t=const, но учитывает ещё турбулентные пульсации. Тогда в формуле (1.55) вместо D надо принимать (D+Dт). Модель проницания можно использовать для массоотдачи в слой ограниченной толщины, если толщина слоя намного больше

Недостаток модели: трудность определения t. Так, в насадочном аппарате при стекании жидкой пленки с одного насадка на другой можно допустить ее полное перемешивание .В этом случае в качестве времени контакта t можно использовать время стекания пленки по отдельному элементу насадки.