Н.Х. Зиннатуллин
Массообменные процессы и аппараты
Конспекты лекции
Казань, 2012
1 МАССООБМЕН.
1.1 Фазовые равновесия.
Основная задача химико-технологического процесса состоит в направленном изменении макроскопических свойств участвующих в процессе веществ: состава, агрегатного состояния, давления P и температуры Т. При этом происходит перенос субстанций: массы, энергии, импульса. Предельное состояние системы – подвижное равновесие, при котором не происходит изменений макроскопических свойств веществ. Равновесным называют такое состояние системы, при котором перенос субстанций отсутствует.
В изолированной системе условия равновесия определяется только внутренними условиями и записываются так:
,
,
(1.1)
Здесь,
– химический потенциал
-того
компонента.
Условия (1.1) называют условиями механического, термического и химического равновесия.
Все самопроизвольные процессы сопровождаются увеличением энтропии системы. В состоянии равновесия энтропия достигает максимального значения:
(1.2)
Таким образом, условия равновесия системы определяются уравнениями (1.1) и (1.2).
Для открытой системы равновесное состояние может быть устойчивым лишь при её равновесии с окружающей средой. Движущая сила процессов переноса возникает вследствие отклонения от равновесия в самой системе или в окружающей среде. Все технологические схемы является открытыми системами.
Химический потенциал зависит не только от концентрации данного компонента, но и от вида и концентрации других компонентов системы.
Химический потенциал компонента непосредственно изменить невозможно. Для его расчета используют соотношения между термодинамическими функциями, которые, в свою очередь, зависят от состава смеси. Поэтому в инженерных расчетах для определения движущей силы процесса используют разность концентраций.
Возможное существование данной фазы в равновесии с другими определяется по закону равновесия фаз Гиббса:
(1.3)
Здесь
С – число степеней свободы (Р,Т и
концентрация) – минимальное число
параметров, которые можно изменять
независимо друг от друга, не нарушая
равновесие данной системы;
– число фаз системы;
–
число независимых компонентов системы;
– число внешних факторов, влияющих на
положение равновесия в данной системе.
Для процессов
переноса массы
=2
( давление и температура).Правило фаз
Гиббса определяет возможность
существования фаз, но не указывает на
количественных зависимостей переноса
вещества между фазами.
Обычно зависимости между параметрами строят в плоских координатах. Такие диаграммы называются фазовыми.
Для
бинарной смеси строят следующие фазовые
диаграммы:
–
при Т=const,
Т–
при
=const,
y(x)–
при T=const,
y-x
при
=const.
Здесь
- концентрация, y и x – концентрация вещества в фазах.
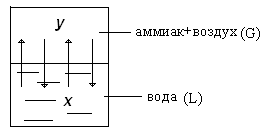
Рис.1.1. Схема массообменного процесса.
Рассмотрим пример поглощения аммиака чистой водой из аммиачно-воздушной смеси: у - концентрация аммиака в воздухе, х - концентрация аммиака в воде. Аммиак - распределяемый компонент. С началом растворения аммиака в воде начнётся переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде. С течением времени скорость переноса аммиака в воду будет снижаться, а скорость обратного переноса возрастать. Такой двусторонний перенос будет продолжаться до установления динамического равновесия – когда переходы в обоих направлениях будут равны.
При равновесии достигается определённая зависимость между равновесными концентрациями распределяемого вещества в фазах при Т и = const:
,
(1.4)
где у* - равновесная концентрация аммиака в воздухе, при концентрации аммиака в воде х.
Графическое изображение зависимости (1.4) и есть линия равновесия. Эту зависимость представим в виде:
у* = mx (1.5),
где m – коэффициент распределения.
Для двухкомпонентной двухфазной системы коэффициент распределения будет зависеть от двух переменных m=f(T,x)=f( ,x)=f( ,T).
Следовательно, необходимо иметь набор экспериментальных данных по равновесию по всей области изменения двух параметров. При увеличении числа компонентов в системе ситуация ещё более усложняется. При отсутствии таких экспериментальных данных для определения коэффициента распределения можно использовать аналитические зависимости. Такие зависимости рассмотрены у А.И. Разинова и В.Б. Когана. Конкретный вид равновесия (1.5) различен для разных процессов массообмена. Например, для абсорбции равновесие описывается законом Генри, для ректификации – законом Рауля и т.д. Зная линию равновесия и рабочую линию для конкретного процесса можно определить направление и движущую силу массообмена в любой точке аппарата.
1.2 Материальный баланс.
В стационарных условиях закон сохранения массы для всего аппарата в виде материального баланса может быть представлен:
(1.6)
,
– соответственно, расходы жидкой и
газовой фаз; х, у – концентрация
распределяемого компонента в фазах; н
– начальное, к – конечное состояние.
Материальный баланс по распределённому компоненту при отсутствии химических реакций имеет вид:
(1.7)
В
случае постоянства расходов
и
уравнение (1.7) упрощается:
(1.8)
Для элементарного участка аппарата имеем:
– dy= dx (1.9)
Знак минус свидетельствует о противоположном изменении концентрации распределяемого компонента в фазах, если в одной фазе увеличивается, то в другой – наоборот, уменьшается.
1.3 Уравнения рабочих и равновесных линий.
Предположим,
что перенос распределяемого компонента
происходит из фазы
в фазу
.
Рис.1.2. Схема массообменного процесса в противоточном аппарате.
Из уравнения материального баланса можно получить уравнение рабочей линии.
Уравнение материального баланса для нижней части аппарата до сечения А-А:
(1.10)
поступает расходуется
Находим
из (1.10) у:
В случае постоянства расходов и получим:
(1.11)
Полученное уравнение (1.11) является уравнением рабочей линии и представляет собой уравнение прямой линии.
Аналогичным образом может быть получено уравнение рабочей линии для прямоточного аппарата.
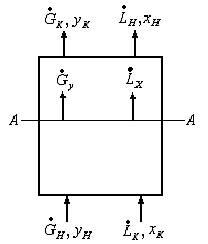
Рис.1.3. Схема массообменного процесса в прямоточном аппарате
(1.12)
поступает расходуется
Находим
из (1.12) у:
,
если расходы не меняются, т.е.
и
=const,
то:
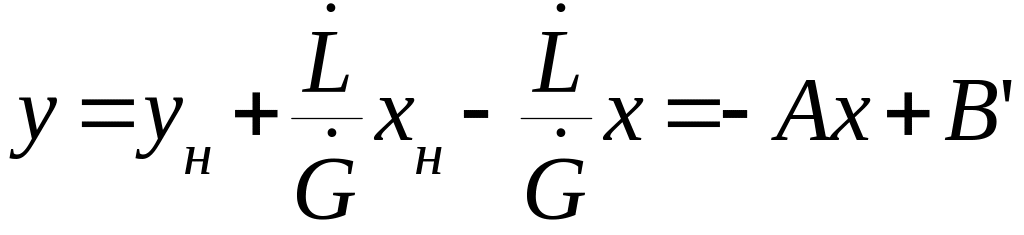(1.13)
а б
Рис.1.4. Рабочие линии: а – противоток, б – прямоток.
Запишем уравнение равновесной линии, связывающее рабочую концентрацию распределяемого компонента в одной из фаз с его равновесной концентрацией в другой фазе. Под равновесной концентрацией в произвольном сечении аппарата понимают концентрацию компонента в фазе, находящейся в равновесии с другой, состав которой определяется рабочей концентрацией. Уравнение равновесной линии:
у*=mх (1.14)
Здесь у* - равновесная концентрация в фазе G, х – рабочая концентрация в фазе L,
m – коэффициент распределения.
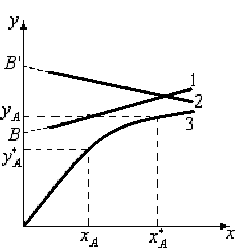
Рис.1.5. Рабочие (1 и 2) и равновесная (3) линии.
Рабочая
концентрация распределяемого компонента
в фазе G
превышает равновесную. Поэтому
распределяемый компонент будет переходить
из G
фазы во вторую фазу L,
до равновесия т.к.
.