5.6.3. Линия без потерь при реактивной нагрузке

Решение телеграфных уравнений имеет вид

,

Рассмотрим напряжение в линии (ток проанализируйте самостоятельно):

,

.

Для амплитуды получим

,

Зависимости показаны на рис. 5.10.

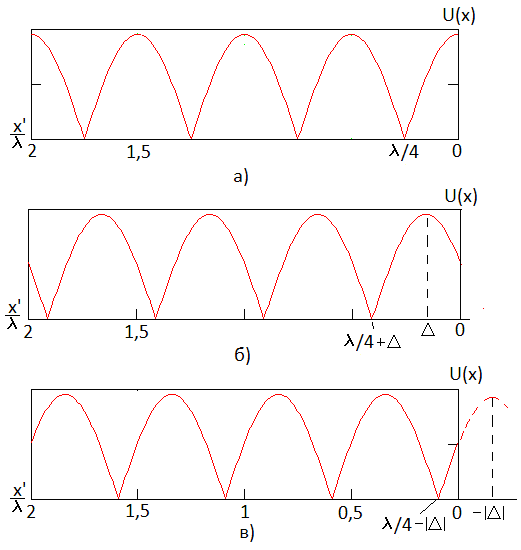
Рис. 5.10

Как видно, при подключении реактивной нагрузки происходит смещение узлов и пучностей тока и напряжения. На рис. 5.10а показана зависимость для разомкнутой на конце линии. При подключении к линии емкостной нагрузки (рис. 5.10б)

с отрицательным реактивным сопро-тивлением происхо-дит смещение узлов и пучностей в сторону генератора ( ). При этом линия как будто становится короче (укорочение длин-ной линии), как по-

Рис. 5.11 казано на рис. 5.11.

Аналогично, при подключении к разомкнутой диной линии индуктивности происходит ее удлинение (рис. 5.10в).

Смещение узлов и пучностей можно использовать для измерения неизвестных индуктивностей и емкостей. Например, если при подключенной емкости к разомкнутой длинной линии узел напряжения сместился к источнику на величину , то значение емкости определится из уравнения

,

тогда

или .

Если в короткозамкнутой линии вместо замыкателя подключить индуктивность L, то узлы и пучности сместятся ближе к нагрузке на расстояние

Полученное выражение следует из того, что индуктивность L можно заменить отрезком короткозамкнутой линии длиной .

5.6.4. Линия без потерь при несогласованной активной нагрузке

Рассмотрим напряжение в линии при несогласованной активной нагрузке ,

,

тогда для амплитуды (модуля) получим при

При получим , как это имеет место в режиме бегущих волн. Зависимости для различных показаны на рис. 5.12.

Рис. 5.12

Как видно из рис. 5.12, при несогласованном режиме работы длинной линии имеют место и падающая и отраженная волны.

5.7. КСВ и КБВ

Соотношение между амплитудами стоячей и бегущей волн в длинной линии характеризуется коэффициентом бегущей волны (К_БВ)

или коэффициентом стоячей волны (К_СВ)

где U_min и U_max - соответственно наименьшая и наибольшая амплитуды напряжения вдоль линии. На рис. 5.12 К_БВ=0,5, а К_СВ=2.

В длинной линии без потерь при активной нагрузке R_н можно записать

Эти коэффициенты легко измеряются, тогда, зная волновое сопротивление линии , можно измерять активное сопротивление неизвестной нагрузки.

Величина К_СВ широко используется как мера близости режима работы линии к согласованному.

5.8. Входное сопротивление линии

Входное сопротивление Z_вх линии в этом случае определяется выражением т(получите его самостоятельно)

При R_н=Z_с (в режиме бегущих волн) входное сопротивление линии равно характеристическому Z_вх=Z_с, а, например, при коротком замыкании линии (R_н=0) входное сопротивление реактивно и равно

.

Зависимость от показана на рис. 5.13.

Рис. 5.13

Как видно, по мере удаления от короткозамкнутой нагрузки входное сопротивление линии без потерь становится сначала индуктивным, потом емкостным и т.д.

Волновое сопротивление двухпроводной длинной линии, размещенной в вакууме (в воздухе) активно и равно

где d - радиус проводов линии, D - расстояние между центрами проводов линии.

5.9. Применение длинной линии

5.9.1. Фидер

Фидер предназначен для передачи сигнала от источника в нагрузку (рис. 5.14).

Рис. 5.14

Если длина фидера соизмерима с длиной волны , то он является длинной линией.

,

где - фазовая скорость, в вакууме - скорость света.

В длинной линии присутствуют потери мощности сигнала и его уровень падает при удалении от источника,

,

- коэффициент затухания с размерностью 1/м, часто используется размерность Дб/м. Зависимость показана на рис. 5.15

Рис. 5.15

Например, если в коаксиальном кабеле затухание равно =0,1 Дб/м, то для фидера длиной L=100 м затухание сигнала составит 10 Дб или 10 раз по мощности, а по напряжению раза. Чем длиннее фидер, тем выше затухание.