36. Математическая модель задачи, двойственной задаче об использовании ресурсов.

Задача об использовании ресурсов в общем виде.

- прибыль от реализации одной единицы продукции.

, - норма расхода ресурса i-ого вида на производство одной единицы продукции j-ого вида, - количество ресурсов по i -ому виду ресурсов (i=1…n), x1, xn≥0

Двойственная задача: Предположим, что некоторая организация решила закупить ресурсы (S1…Sn) предприятия и необходимо установить оптимальные цены на эти ресурсы. Y1..Ym- цены ресурсов. Р1…Pn – предприятия. Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы в количестве были минимальными, т е с точки зрения покупающей организации – целевая функция:

С другой стороны, предприятие, продающее ресурсы заинтересовано в том, чтобы полученная выручка была не меньше той суммы, которую предприятие может получить при переработки ресурсов в готовую продукцию.

- сумма денег, которую получить продающее предприятие, когда оно продаст ресурсы, идущие на производство 1-ой единицы продукции первого вида Р1.

Исходная задача:

Двойственная задача: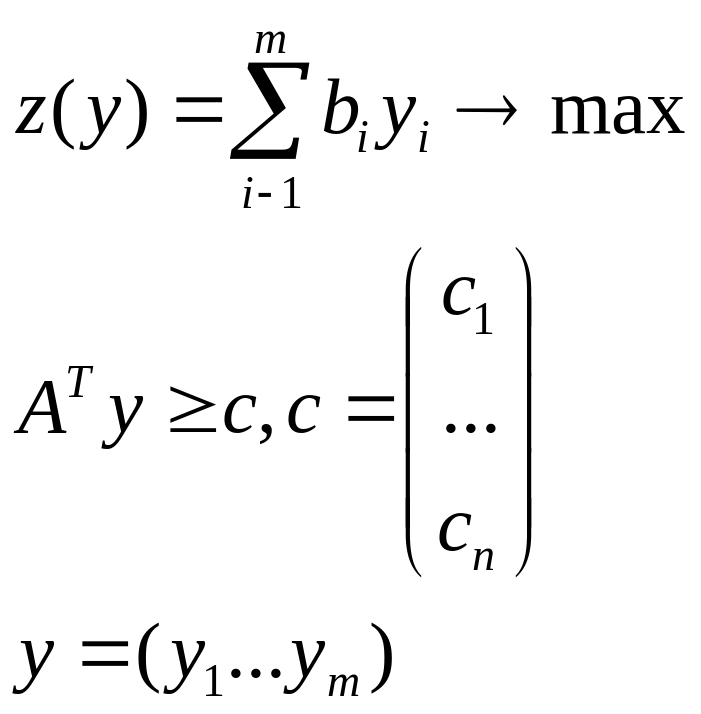

37. Общий правила составления двойственных задач.

1) в общей задаче ищут max целевой функции, в другой – min

2) коэффициенты при переменных целевой функции одной задачи являются свободными членами системы ограничений другой задачи

3) Матрицы коэффициентов при переменных в системе ограничений в обеих задачах являются транспонированными друг к другу.

4) Число неравенств в одной задаче совпадает с числом переменных в другой задаче

5) Каждая из задач представлена в стандартной форме, причем в задаче максимизации, все неравенства вида ≤, а в минимизации - ≥

6) условие неотрицательности переменных имеются в обеих задачах

38. Первая (основная) теорема двойственности и ее экономический смысл.

Теорема: Если одна из взаимосвязанных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их целевых функций = между собой. , - оптимальное решение исходной задачи - оптим решение двойственной задачи..

Если целевая функция одной из задач не ограничена, то условия системы ограничений другой задачи противоречивы (т е область доп решений является пустой). Обратное утверждение в общем случае неверно, т е из того что условие одной задачи противоречиво, не следует того, что целевая функция другой задачи будет неограниченна.

Эконом смысл План производства и набор цен ресурсов оказываются оптимальными только тогда , когда выручка от реализации продукции, найденная при «внешних» (известных заранее) цен затратам на ресурсы по «внутренним» (определяемым только из решения задач) ценам . Для всех же других планов х,y прибыль от реализации продуктов всегда ≤ затрат на ресурсы.

Можно и так интерпретировать эк смысл: Предприятию безразлично производить ли продукцию и получить max прибыль, либо продавать ресурсы по ценам и возместить от продажи равные ей min затраты на ресурсы.