1. Понятие n- мерного вектора, основные определения.

Определение. Упорядоченная совокупность чисел называется n-мерным вектором. Числа   называются координатами вектора.

Векторы обозначаются строчными латинскими буквами, например, a, b, c и т.п., координаты вектора указываются в скобках. Если записать вектор a как  , то имеем вектор-строку; если записать  , то имеем вектор-столбец. Это две формы записи одного и того же объекта - n-мерного вектора.

Вектор  , все координаты которого равны нулю, называют нулевым вектором.

Вектор   называется противоположным вектору  .

Для n-мерных векторов задаются две операции: сложение векторов и умножение вектора на число.

Определение.

Суммой двух векторов   и   называется вектор, координаты которого равны сумме соответствующих координат, то есть,  .

Следует отметить, что складывать можно только векторы количество координат которых совпадает. Операция сложения для векторов, имеющих различное число координат, не определена.

Определение.

Произведением действительного числа λ и вектора   называется вектор, координаты которого равны соответствующим координатам вектора а, умноженным на  λ , то есть,  .

2. Операции над векторами, основные свойства операций.

1. А + В = {а1 + в1, а2 + в2,…аn + вn }

2. α * А = (αА1, α А2… αАn.)

Для любых векторов справедливы свойства:

1. a + b = b + a;

2. (a + b) + c = a + (b + c) - ассоциативный

3.  a + 0 = a;

4. а * 0 = 0

5. a + (-a) = 0;

6.  α * (А+В) = α* А + α* В

7. (α + β) * А = α* А + β* А

3. Скалярное произведение

1. (А,В) = (В,А)

2. (А + В);C = (А;С)+ (В;С)

3. (αА;В)= α *(А;В)

4. (А;А)≥0, = 0, если А=0

Множество всех n-мерных векторов с введенными операциями сложения векторов и умножения вектора на число порождают линейное пространство.

3. Понятие линейной зависимости системы векторов.

            Определение. Система векторов (*)   называется линейно зависимой, если один из них, безразлично какой, линейно выражается через остальные.

            Определение 2.Система (*) – линейно зависимая, если существуют такие числа λ1, λ2… λm ≠ 0 одновременно при которых линейная комбинация

4. Эквивалентность двух определений линейной независимости.

Определение 1. Система векторов (*)   называется линейно зависимой, если один из них, безразлично какой, линейно выражается через остальные.

            Определение 2.Система (*) – линейно зависимая, если существуют такие числа λ1, λ2… λm ≠ 0 одновременно при которых линейная комбинация

1. Опр 1 → Опр 2

Дано: система линейна зависима смысле (1), т е

2. Опр2→Опр1

векторы линейно независимы смысле (2)

Одновременно существует

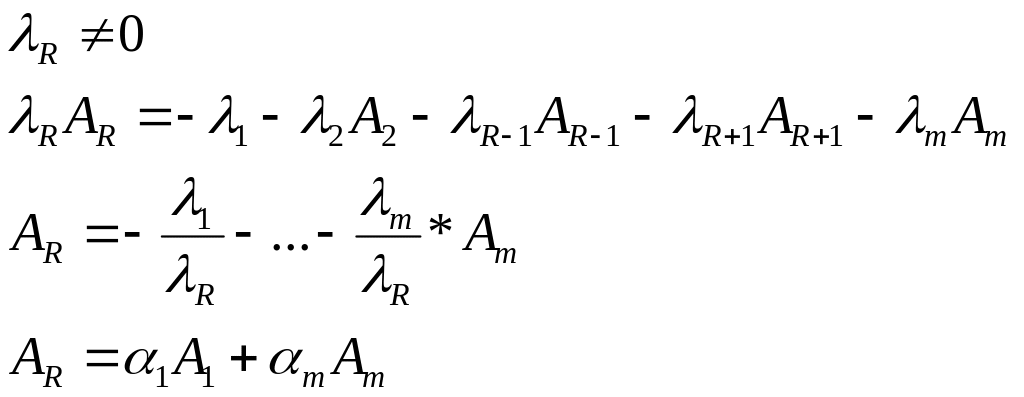
5. Лемма о линейной зависимости системы векторов, содержащей нулевой вектор.

Если среди векторов имеется нулевой вектор, то такая система является линейно зависимой.

6. Лемма о линейной независимости диагональной системы векторов.

Диагональная система векторов всегда линейно независима.

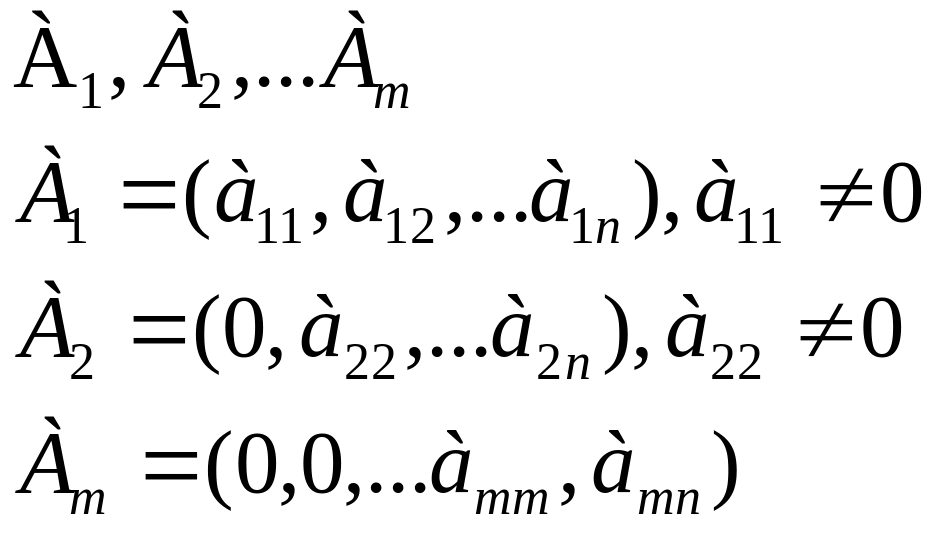
Линейная комбинация, составленная из , только при условии, что - линейно независимая система векторов. Док-во:

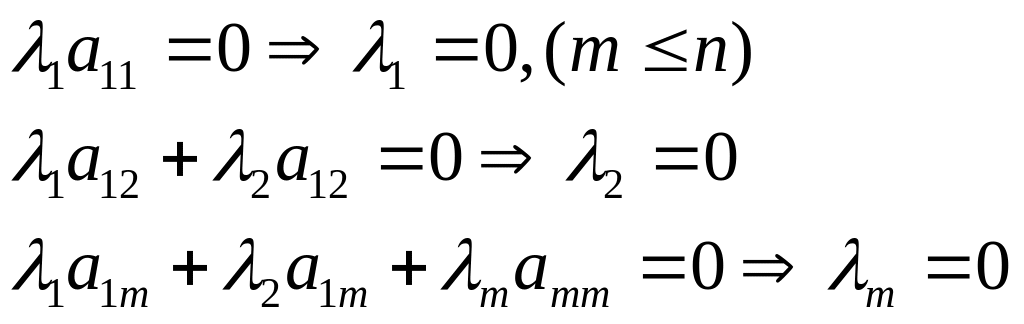Следовательно система -линейно независимая.