3.Метод интегрирования по частям
Теорема.
Пусть функции u(x)
и v(x)
определены и дифференцируемы на некотором
промежутке X
и пусть функция u′(x)
v(x)
имеет первообразную на этом промежутке,
т.е. существует
Тогда на промежутке X
функция
u′(x)
v(x)
также имеет первообразную и справедлива
формула
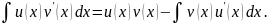(2)
Пример
3. Вычислить
интеграл
Решение.
Положим
Тогда
(здесь
в качестве
можно взять любую из первообразных вида
x+C,
где
C
произвольная
постоянная. Мы взяли
,
т.е. C=0).
По формуле имеем
Так как
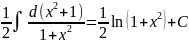
то окончательно получаем
Формула
Ньютона-Лейбница:
Геометрический смысл определенного интеграла
Итак,
неопределенный интеграл от неотрицательной
непрерывной функции
на [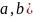
численно равен площади криволинейной
трапеции с основанием [
,
ограниченной сверху графиком функции
y=
.
В этом заключается геометрический смысл
определенного интеграла.
Тема 3.1. Неопределенный интеграл
1)Исследовательская работа, решение задач
Упражнения. Вычислить следующие интегралы:
1.
10.
2.
11.
3.
12.
4.
13.
5.
14.
6.
15.
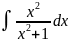
7.
16.
8.
17.
9.
18.
?Вопросы для самопроверки
1. В чем состоит метод непосредственного интегрирования?
2. Напишите формулу замены переменной в неопределенном интеграле. При каких условиях эта формула справедлива?
3. Напишите формулу интегрирования по частям. При каких условиях эта формула справедлива?
4. Какие интегралы наиболее удобно вычислять интегрированием по частям?
5. Каково назначение рекуррентных формул?
Контрольные задачи к разделу
Применяя метод замены переменной, вычислить следующие интегралы:
3.1.1.
3.1.
2.
3.1.3.
3.1.4.
3.1.5.
3.1.6.
3.1.7.
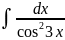3.1.8.
3.1.9.
3.1.10.
3.1.11.
3.1.12.
3.1.13.
3.1.14.
3.1.15.
3.1.16.
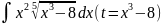
3.1.17.
3.1.18.
3.1.19.
3.1.20.
3.1.21.
3.1.22.
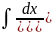
С помощью метода интегрирования по частям вычислить следующие интегралы:
3.1.23.
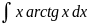3.1.24.
3.1.25.
3.1.26.
3.1.27.
3.1.28.
3.1.29.
3.1.30.
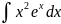
3.1.31.
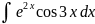3.1.32.
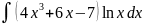
3.1.33.
3.1.34.
