
Математика
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования žКузбасский государственный технический университет имени Т.Ф. Горбачева¤
Составитель Николаева Е.А.
МАТЕМАТИКА
Методические указания к контрольным работам №1 и №2
Рекомендовано учебно-методической комиссией направления подготовки 081100.62 žГосударственное и муниципальное управление¤ в качестве электронного учебного издания для самостоятельной работы
КЕМЕРОВО 2013
Рецензенты:
Фадеев Ю. А. - профессор кафедры математики.
Заруба Н. А. - председатель учебно-методической комиссии направления подготовки 081100.62 žГосударственное и муниципальное управление¤.
Николаева Евгения Александровна. Математика. [Электронный ресурс]: методические указания к контрольным работам №1 и №2 для студентов 1 курса (1,2 семестр) направления подготовки 081100.62 žГосударственное и муниципальное управление¤ заочной формы обучения / Составитель: Е. А. Николаева. – Электрон. дан. – Кемерово : КузГТУ, 2013. – Систем. требования: Pentium IV; ОЗУ 8 Мб; Windows 97; мышь. ‒ Загл. с экрана.
Методические указания предназначены помочь студентам заочникам выполнить контрольные работы по дисциплине žМатематика¤.
Методические указания содержат программу, примеры решенных заданий, контрольные работы и список литературы.
КузГТУНиколаева Е.А.
1
Контрольные работы составлены в соответствии с программой курса математики для студентов-заочников.
Номера заданий контрольной работы студент должен выбрать по таблице žВыбор варианта контрольной работы¤ следующим образом: номер варианта определяется по последней цифре зачетной книжки (0-9)
Контрольные работы, выполненные не по своему варианту, возвращаются непроверенными.
Выбор варианта контрольной работы
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
Контрольная работа №1 |
|
|
|
|
|
|
|
|||
Задание 1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
1.10 |
Задание 2 |
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
2.6 |
2.7 |
2.8 |
2.9 |
2.10 |
Задание 3 |
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
3.9 |
3.10 |
Задание 4 |
4.1 |
4.2 |
4.3 |
4.4 |
4.5 |
4.6 |
4.7 |
4.8 |
4.9 |
4.10 |
Контрольная работа №2 |
|
|
|
|
|
|
|
|||
Задание 1 |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
1.10 |
Задание 2 |
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
2.6 |
2.7 |
2.8 |
2.9 |
2.10 |
ПРОГРАММА 1 КУРСА (1 СЕМЕСТР)
1 АЛГЕБРА
1.1.Математическая символика. Определители. Свойства определителей
1.2.Системы линейных уравнений – инструмент построения организационно-управленческих моделей. Метод Крамера. Метод Гаусса.
1.3.Матричное моделирование в задачах управления. Понятие матрицы. Основные операции над матрицами и их свойства. Ранг матрицы.
2 МАТЕМАТИЧЕСКИЙ АНАЛИЗ
2
2.1.Понятие функции. Способы задания. Основные элементарные функции. Сложные функции. Характеристики функций.
2.2.Предел функции. Свойства пределов. Сравнение бесконечно малых, бесконечно больших функций.
2.3.Приращение аргумента. Приращение функции. Производная функции. Таблица производных основных элементарных функции. Правила дифференцирования.
2.4.Приложение производной. Дифференциал функции. Экстремум. Наибольшее и наименьшее значения функции на отрезке. Функции в задачах экономики и управления.
2.5.Понятие первообразной. Неопределенный интеграл. Таблица интегралов
2.6.Определенный интеграл. Приложения определенного ин-
теграла
3.ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
3.1.Понятие математической модели. Задача математического программирования в принятии управленческих решений. Задача линейного программирования.
3.2.Графический метод решения задачи линейного программирования. Пример построения модели принятия реше-
ния.
ПРОГРАММА 1 КУРСА (2 СЕМЕСТР)
4.ТЕОРИЯ ВЕРОЯТНОСТЕЙ
4.1.Основные понятия теории вероятностей. Испытание. Событие. Виды событий. Классическая формула вероятности.
4.2.Алгебра событий. Сложение событий, умножение событий. Вероятность композиции событий. Условная вероятность. Формула полной вероятности. Формула Бейеса.
4.3.Случайные величины. Закон распределения дискретной случайной величины. Функция распределения. Функция плотности распределения. Числовые характеристики случайных величин
3
5.МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
5.1.Методы математической статистики в решении типовых организационно-управленческих задач. Транспортная задача, сетевое планирование-математические модели принятия решений.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ №1
При решении задачи 1 нужно использовать элементы линейной и векторной алгебры [1, гл. 2, с.53-61, с. 82-89].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Пример. Показать, что векторы a |
|
|
||||||||||||||
|
|
1;2;0 ; b |
|
2;1; 1 ; |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
c |
образуют базис и |
найти |
координаты |
вектора |
||||||||||||||
|
3; 1;2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
в этом базисе. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
0;4;1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Решение. Вычислим определитель, составленный из коор- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
динат векторов a,b, c : |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
1 |
1 |
|
3. |
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Так как определитель отличен от нуля, то векторы a,b, c |
||||||||||||||||
образуют базис и вектор e можно разложить в данном базисе: |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
e a b c . |
|
|
|
|
|
||||||||
Это векторное равенство равносильно системе трёх уравнений с тремя неизвестными , , :
1 2 3 0
2 1 1 4
0 1 2 1.
Решим систему по формулам Крамера. Вычислим определители
|
|
0 |
2 |
3 |
|
|
|
1 |
0 |
3 |
|
|
|
1 |
2 |
0 |
|
|
|
4 |
1 |
1 |
3; |
|
|
2 |
4 |
1 |
15; |
|
|
2 |
1 |
4 |
9 . |
|
|
1 |
1 |
2 |
|
|
|
0 |
1 |
2 |
|
|
|
0 |
1 |
1 |
|
По формулам Крамера находим:
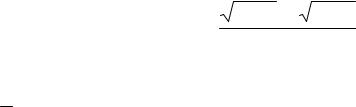
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
15 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
1; |
|
|
|
|
|
5; |
|
|
|
|
|
3 . |
|
|
|
|
3 |
|
|
|
|||||||||||
|
|
3 |
|
|
|
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение системы и есть координаты вектора e в базисе a,b, c , то |
|||||||||||||||||
есть: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
e a 5b |
3c . |
|
|
|
|
|
|||
При решении задачи 2 следует познакомиться с методами нахождения пределов функций [1, гл. 5, п. п. 1, 2], [3, гл. 6, п. п. 1-6]. Рассмотрим некоторые из них.
Пример. Найти lim |
7x4 3x2 x |
2 |
. |
3x3 2x2 4 |
|
||
x |
|
|
Решение. Для нахождения предела отношения двух многочленов относительно x при x каждый многочлен делят на
xn , где n – наивысшая степень этих многочленов. |
|
||||||||||||||||
|
|
|
|
|
3 |
|
|
1 |
2 |
|
|||||||
|
|
7x4 3x2 x 2 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||
lim |
lim |
x2 |
x3 |
x4 |
, |
||||||||||||
|
3 2 |
|
4 |
|
|||||||||||||
x |
3x3 2x2 4 |
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a |
|
|
|
x |
x2 |
|
x4 |
|
||||||||
так как lim |
0 , где a const, n 0. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
x xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. Найти lim 3 2 x 3 2 x .
x 0 3x
Решение. Предельный переход даёт нам неопределённость
0
, от которой избавляемся переводом иррациональности из
0
числителя |
в |
знаменатель. |
Используем |
формулу |
a 3 b3 a b a 2 ab b2 . Получим

5
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
3 |
|
|
3 |
4 |
x |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
. |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
2 |
|
|
|
3 3 3 4 |
9 |
|
|
||||||||||||||||||||||||||||||||||||
x 0 |
|
|
|
3 |
|
|
|
3 |
|
|
4 x |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
вычислении пределов, |
|
|
|
|
содержащих |
|
тригонометриче- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ские функции, для раскрытия неопределённости |
|
|
|
используют |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
первый замечательный предел lim |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Найти lim |
cos 5x cos2 5x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 5x 1 cos 5x |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 5x |
|
cos |
|
|
5x |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Решение. x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 sin2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
lim cos 5x lim |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 2 lim |
|
|
2 |
|
|
2 |
12,5 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
x 0 |
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
1 x |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Второй |
|
|
замечательный |
|
предел |
|
|
|
|
вида |
lim 1 |
|
|
|
|
e или |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim 1 x |
|
e используют при раскрытии неопределённости ви- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да 1 .
x 3 2x
Пример. Вычислить lim . x x 1
Решение.
x |
|
|
2x |
|
|
x 1 |
4 |
|
2x |
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
lim |
|
|
|
|
lim |
|
|
|
|
lim |
1 |
|
|
|
|
|
x 1 |
||||||||
x x 1 |
x |
|
|
x |
|
|
||||||
|
|
x 1 |
|
4 |
2x |
|
|
|
|
||
4 4 |
x 1 |
||||
|
|
. |
|||
|
|||||
x 1 |
|
|
|||

6
Введём новую переменную x 1 t , тогда при x , t ,
4
получим
|
|
|
|
|
|
lim |
8x |
|
|
|
|
|
|
|
|||
|
|
1 t x x 1 |
||||||
lim |
1 |
|
|
|
|
|||
|
||||||||
|
t |
|
|
t |
|
|||
|
|
|
|
|
|
|
||
lim 8x
ex x 1 e8 .
Задание 3. Исследовать функцию на непрерывность. В этом задании необходимо учитывать, что все элементарные функции непрерывны в своей области определения. Непрерывность нарушается в тех точках, где функция не определена [3, гл. 5, п. 2; 5, гл. 13, 14, п. 103–108; 6, гл. 6, п. 6; 8, гл. 2, п. 9–11].
|
|
|
|
|
6 |
|
||
|
|
|
f x 3 |
|
|
|||
Пример. Установить, является ли функция |
4 x 5 |
|||||||
непрерывной при значениях аргумента x |
5 |
и |
x 1. |
|||||
|
||||||||
|
5 |
4 |
|
|
|
|
||
Решение. При x |
знаменатель дроби обращается в нуль, |
|||||||
|
||||||||
4 |
|
|
|
|
|
|
||
и функция не определена, следовательно, точка x 5 есть точка 4
разрыва. Установим тип разрыва, для чего найдем пределы слева и справа при x 5 .
|
|
|
|
|
4 |
|
|
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
|
|
Предел справа |
lim |
|
|
|
|
|
, так как в знаменате- |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
5 |
0 4x 5 |
|
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ле |
положительная |
|
|
бесконечно |
|
|
малая |
величина. Отсю- |
|||||||||||||
|
|
6 |
3 . |
|
|
|
|
|
|
|
|
|
|||||||||
да |
lim 34 x 5 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
5 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
||
|
Предел слева |
lim |
|
|
|
|
|
, |
так как в знаменате- |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
5 |
0 4x 5 |
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ле отрицательная бесконечно малая величина, тогда
7
|
|
|
6 |
3 |
1 |
|
||
lim |
3 |
4 x 5 |
0 . |
|||||
3 |
||||||||
x |
5 |
0 |
|
|
|
|
||
|
|
|
|
|
||||
4 |
|
|
|
|
|
|
||
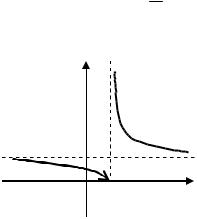
Точка x 5 есть точка разрыва второго рода. Схематиче- 4
ский чертеж графика данной функции изображен на рисунке.
y |
|
|
При x 1: |
f 1 3 6 |
1 |
, |
|
||||
|
|
|
|
||||||||
|
|
|
|
|
729 |
|
|
||||
|
|
|
|
f x lim |
6 |
3 6 |
1 |
|
|||
|
|
|
lim |
3 |
4 x 5 |
. |
|||||
|
|
|
|
||||||||
|
|
|
x 1 |
x 1 |
729 |
|
|||||
|
5 |
x |
Следовательно, при x 1 функция |
||||||||
непрерывна (предел функции справа |
|||||||||||
4 |
|
и слева совпадает со значением |
|||||||||
|
|
|
функции при x 1). |
||||||||
При решении задачи 4 следует познакомиться с графическим методом решения задачи линейного программирования [6].
Пример. Определить точку максимума, вычислить ее коор-
динаты и значение целевой функции в ней
f(x) = 2 x1 + 3 x2 max
x1 + 3 x2 18,
2 x1 + x2 16,
x2 5,
3 x1 21,
x1 0, x2 0
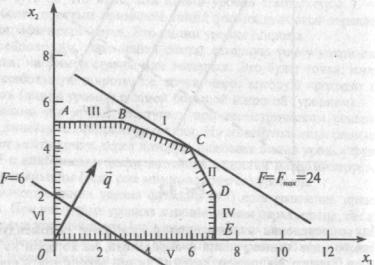
Изобразим многоугольник решений
8
Очевидно, что при f = 0 линия уровня 2 x1 + З x2 = 0 проходит через начало координат. Зададим, например, f = 6 и построим линию уровня 2 x1 + 3 x2 = 6. Ее расположение указывает на направление возрастания линейной функции (вектор q ). Так как рассматриваемая задача – на отыскание максимума, то оптимальное решение – в угловой точке С, находящейся на пересечении прямых I и II, т.е. координаты точки С определяются реше-
x1 3x 2 18
нием системы уравнений 2x1 x 2 16 откуда x1 = 6, х2 = 4, т.е.
С(6;4)
Максимальное значение функции fmax = 2*6 + 3*4 = 24.
