
- •Раздел 1. Линейная алгебра
- •Тема 1.1. Матрицы и определители
- •1) Написание рефератов, докладов
- •2)Создание презентаций
- •Тема 1.2. Система линейных уравнений
- •1)Исследовательская работа. Решение задач
- •Раздел 2. Дифференциальное исчисление функцции
- •Основные положения теории пределов
- •7. При решении многих задач используются следующие эквивалентности, верные при X→0:
- •8. Операции над пределами функций
- •Тема 2.1. Функции, пределы, непрерывность
- •1) Написание рефератов, докладов
- •Исследовательская работа. Решение задач
- •Тема 2.2 Дифференциальное исчисление
- •1)Написание рефератов, докладов
- •2)Исследовательская работа. Решение задач
- •Тема 2.3 Применение дифференциального исчисления к исследованию функций
- •Разработка алгоритма построения графиков функций
- •?Вопросы для самопроверки
- •Раздел 3. Интегральное исчисление функции одной действительной переменной
- •1.Непосредственное интегрирование
- •2.Метод подстановки
- •3.Метод интегрирования по частям
- •Тема 3.1. Неопределенный интеграл
- •1)Исследовательская работа, решение задач
- •Тема 3.2 Определенный интеграл
- •1)Написание рефератов, докладов.
- •2)Исследовательская работа, решение задач.
- •Контрольные задачи к разделу
?Вопросы для самопроверки
1.Дайте определения локального экстремума функции.
2. Может ли функция иметь несколько локальных экстремумов?
3. Может ли локальный максимум некоторой функции оказаться меньше какого-то локального минимума этой же функции?
4. Сформулируйте теорему, выражающую необходимое условие локального экстремума. Покажите на примере, что это условие не является достаточным.
5. Какие точки называются точками возможного экстремума функции?
6. Сформулируйте теорему, выражающую достаточное условие локального экстремума.
7. Дайте определение направления выпуклости графика функции.
8. Сформулируйте теорему, с помощью которой решается вопрос о направлении выпуклости графика функции.
9. Дайте определение точки перегиба графика функции.
10. Сформулируйте необходимое условие точки перегиба графика функции. Покажите на примере, что это условие не является достаточным.
11. Какие точки называются критическими?
12. Сформулируйте достаточное условие точки перегиба графика функции.
13. Может ли функция иметь экстремум в точке перегиба графика функции?
14. Дайте определение вертикальной, горизонтальной и наклонной асимптот. Приведите примеры.
15. Докажите следующее утверждение: Если прямая y=kx+b является наклонной асимптотой графика функции y=f(x) при x , существуют пределы
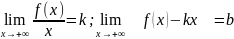
и, обратно, если оба предела существуют, то прямая y=kx+b, является наклонной асимптотой графика функции y=f(x) при x .
16.Приведите схему построения графика функции.
Контрольные задачи к разделу
Проведите полное исследование следующих функций и постройте их графики:
2.3.1.
y=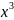 (x-10
;
2.3.
2.
(x-10
;
2.3.
2.
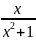 ;
2.3.3.
y=
;
2.3.3.
y=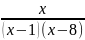 ;
2.3.4.
y=
;
2.3.4.
y=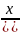 ;
;
2.3.5.
y=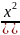 ;
2.3.6.
y=
;
2.3.6.
y=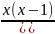 ;
2.3.7.
y=
;
2.3.7.
y=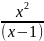 ;
2.3.8.
y=
;
2.3.8.
y=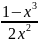 ;
;
2.3.9.
y=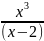 ;
2.3.10.
y=(x+1)
;
2.3.10.
y=(x+1)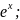 2.3.11.
y=
2.3.11.
y=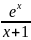 ;
2.3.12.
y=
;
2.3.12.
y=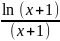 ;
;
2.3.13.
y=(x+1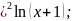
Раздел 3. Интегральное исчисление функции одной действительной переменной
Основные теоретические положения раздела
Основные свойства неопределенного интеграла
1.
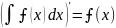 и
и
 2.
2.
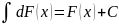 или
или

3.
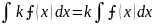
4.
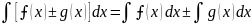
Таблица основных интегралов
I
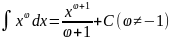
II
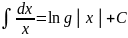
III
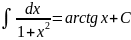
IV
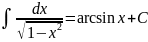
V
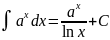
VI
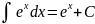
VII
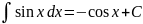
VIII
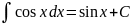
IX
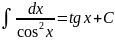
X
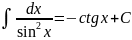
XI

XII
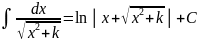
XIII
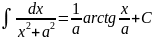
XIV
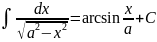
Основные методы интегрирования
1.Непосредственное интегрирование
Пример
1.
Вычислить интеграл
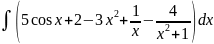
Решение. Применив свойства и
имеем

Далее, используя соответственно формулы VIII, I, II, III таблицы основных интегралов, находим
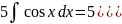
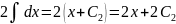 ,
,
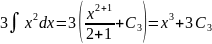
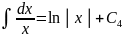 ;
;
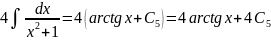 .
.
Таким образом,
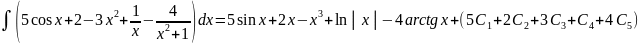
Обычно
все произвольные постоянные суммируют,
результат обозначается одной буквой:
 , поэтому окончательно получаем:
, поэтому окончательно получаем:
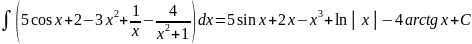
Правильность полученного результата легко проверить дифференцированием. (Сделайте это самостоятельно)
2.Метод подстановки
Теорема.
Пусть
функция
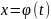 определена и дифференцируема на некотором
промежутке T
и пусть X
- множество значений этой функции, на
котором определена функция
,
т.е. на Tопределена
сложная функция
определена и дифференцируема на некотором
промежутке T
и пусть X
- множество значений этой функции, на
котором определена функция
,
т.е. на Tопределена
сложная функция
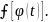 Тогда если на множестве X
функция
имеет первообразную F(x),
то справедлива формула
Тогда если на множестве X
функция
имеет первообразную F(x),
то справедлива формула
 (1)
(1)
Пример
2. Вычислить
интеграл
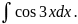
Решение.
Интеграл
не табличный, хотя и напоминает интеграл
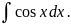 Поэтому для его вычисления естественно
сделать подстановку, полагая
Поэтому для его вычисления естественно
сделать подстановку, полагая
 тогда
тогда
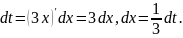 По формуле (1) получаем
По формуле (1) получаем
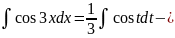 табличный
интеграл. Применяя формулу VIII
таблицы основных интегралов, находим
табличный
интеграл. Применяя формулу VIII
таблицы основных интегралов, находим
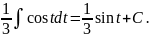
Возвращаясь к переменной x, окончательно получаем

Данный
интеграл можно вычислить и непосредственно,
заменив
dx
через
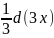 ,
т.е. внося под знак дифференциала
множитель 3
и разделив на него интеграл. В результате
получаем
,
т.е. внося под знак дифференциала
множитель 3
и разделив на него интеграл. В результате
получаем
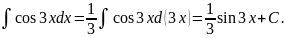
Здесь применена подстановка t=3x. Этот экономный и простой прием будет неоднократно использован в дальнейшем.
