- •Раздел 1. Линейная алгебра
- •Тема 1.1. Матрицы и определители
- •1) Написание рефератов, докладов
- •2)Создание презентаций
- •Тема 1.2. Система линейных уравнений
- •1)Исследовательская работа. Решение задач
- •Раздел 2. Дифференциальное исчисление функцции
- •Основные положения теории пределов
- •7. При решении многих задач используются следующие эквивалентности, верные при X→0:
- •8. Операции над пределами функций
- •Тема 2.1. Функции, пределы, непрерывность
- •1) Написание рефератов, докладов
- •Исследовательская работа. Решение задач
- •Тема 2.2 Дифференциальное исчисление
- •1)Написание рефератов, докладов
- •2)Исследовательская работа. Решение задач
- •Тема 2.3 Применение дифференциального исчисления к исследованию функций
- •Разработка алгоритма построения графиков функций
- •?Вопросы для самопроверки
- •Раздел 3. Интегральное исчисление функции одной действительной переменной
- •1.Непосредственное интегрирование
- •2.Метод подстановки
- •3.Метод интегрирования по частям
- •Тема 3.1. Неопределенный интеграл
- •1)Исследовательская работа, решение задач
- •Тема 3.2 Определенный интеграл
- •1)Написание рефератов, докладов.
- •2)Исследовательская работа, решение задач.
- •Контрольные задачи к разделу
Раздел 1. Линейная алгебра
Тема 1.1. Матрицы и определители
1) Написание рефератов, докладов
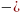 Базис
в пространстве;
Базис
в пространстве;
Нелинейные операции над векторами;
Понятие определителя n-го порядка.
2)Создание презентаций
Декартова прямоугольная система координат в пространстве
Тема 1.2. Система линейных уравнений
1)Исследовательская работа. Решение задач
Линейная однородная система n уравнений с n неизвестными. Метод Гаусса.
Исследовать системы линейных уравнений, для совместных систем найти общее и одно частное решение:
1.
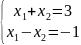 2.
2.
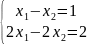
3.
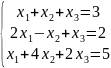 4.
4.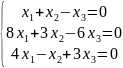
5.
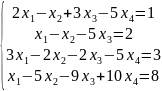 6.
6.
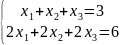
7.
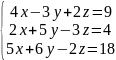 8.
8.
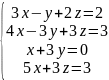
9.
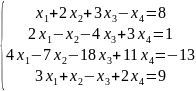 10.
10.
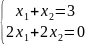
?
Вопросы для самопроверки
1.
Дайте
определение системы m
линейных
уравнений с n
неизвестными
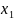 ,
,
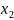 ,
… ,
,
… ,
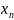 .
.
2. Что называют решением системы m линейных уравнений с n неизвестными?
3. Какая система называется совместной?
4. Какие системы называются эквивалентными?
5. Что значит исследовать систему линейных уравнений?
6. В чем заключается суть метода Гаусса для исследования систем линейных уравнений?
7. К системе линейных уравнений с n неизвестными дописали произвольное уравнение с m неизвестными. Как при этом изменится множество решений системы?
8. Из несовместной системы линейных уравнений удалили какое-то одно уравнение. Будет ли полученная система совместной?
9.
Что
можно сказать о множестве решений
системы линейных уравнений, ранг
r(A)
матрицы этой системы и ранг r(A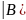 расширенной
матрицы равны нулю?
расширенной
матрицы равны нулю?
10. Может ли частное решение системы линейных уравнений совпадать с её общим решением?
Раздел 2. Дифференциальное исчисление функцции
ОДНОЙ ПЕРЕМЕННОЙ
Основные положения теории пределов
1.Первый замечательный предел:

следствие из первого замечательного предела:
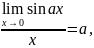 a
a
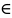 R
R
2.Второй замечательный предел:
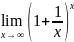 =℮
=℮
следствие из второго замечательного предела:
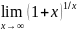 =℮
=℮
3.
Раскрытие
неопределенности вида
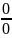
Первое правило Лопиталя:
Если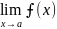 =
=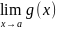 =0, то
=0, то
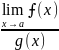 =
=
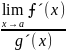
когда последний предел существует (конечный или бесконечный)
4.
Раскрытие неопределенности вида
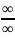
Второе правило Лопиталя:
Если
=
=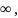 то
то
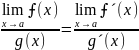
когда последний предел существует (конечный или бесконечный)
5.
Неопределенности вида 0 •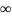 ,
,
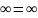 ,
,
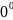 ,
,
 ,
,
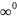 и их раскрытие
и их раскрытие
Неопределенности
вида 0 •
и
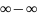 могут быть сведены путем алгебраических
преобразований к неопределенностям
вида
и
,
а затем раскрыты с помощью тождества
могут быть сведены путем алгебраических
преобразований к неопределенностям
вида
и
,
а затем раскрыты с помощью тождества
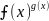 =
=
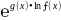
сводятся к неопределенности вида 0•
Например,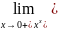

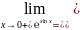
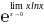 =
=
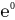 =1
=1
6. Эквивалентными называются бесконечно малые, предел отношения которых равен единице.
Отношение двух бесконечно малых величин можно заменить отношением эквивалентных величин, например,