
- •Года: 04/05;05/06, 06/07; 07/08; 08/09; 09/10, 10/11.
- •2004/2005 Учебный год. Все варианты.
- •2005/2006 Учебный год. Вариант 1.
- •2005/2006 Учебный год. Вариант 2.
- •2005/2006 Учебный год. Вариант 3.
- •2005/2006 Учебный год. Вариант 4.
- •2005/2006 Учебный год. Вариант 5.
- •2006/2007 Учебный год. Вариант I-1.
- •2006/2007 Учебный год. Вариант I-2.
- •2006/2007 Учебный год. Вариант I-3.
- •2006/2007 Учебный год. Вариант I-4.
- •2006/2007 Учебный год. Вариант I-5.
- •2007/2008 Учебный год. Вариант 1.
- •2007/2008 Учебный год. Вариант 2.
- •2007/2008 Учебный год. Вариант 3.
- •2007/2008 Учебный год. Вариант 4.
- •2007/2008 Учебный год. Вариант 5.
- •2008/2009 Учебный год. Вариант II-1
- •2008/2009 Учебный год. Вариант II-2
- •2008/2009 Учебный год. Вариант II-3
- •2008/2009 Учебный год. Вариант II-4.
- •2008/2009 Учебный год. Вариант II-5.
- •2009/2010 Учебный год. Все варианты.
- •2008/2009 Учебный год. Все варианты.
2009/2010 Учебный год. Все варианты.
Задача
1.
Пусть
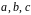 – корни многочлена
.
Вычислить определитель матрицы
– корни многочлена
.
Вычислить определитель матрицы
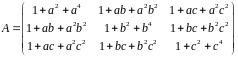 .
.
Вариант
1:
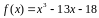 .
Вариант
2:
.
Вариант
2:
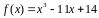 .
Вариант
3:
.
Вариант
3:
 .
Вариант
4:
.
Вариант
4:
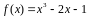 .
Вариант
5:
.
Вариант
5:
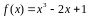 .
.
Решение. Заметим, что матрица раскладывается в произведение матриц:
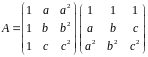
Значит,
ее определитель равен произведению
определителей сомножителей. Поскольку
второй сомножитель – это просто
транспонированный первый, определители
сомножителей будут равны. Поэтому:
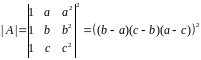
Вариант
1.
Заметим, что
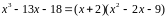 .
Значит,
.
Значит,
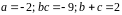 .
.
Тогда
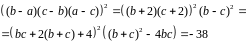 .
.
Вариант
2.
Заметим, что
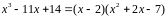 .
Значит,
.
Значит,
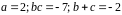 .
.
Тогда
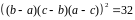 .
.
Вариант
3.
Заметим, что
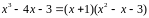 .
Значит,
.
Значит,
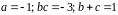 .
.
Тогда
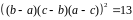 .
.
Вариант
4.
Заметим, что
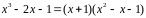 .
Значит,
.
Значит,
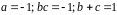 .
.
Тогда
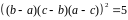 .
.
Вариант
5.
Заметим, что
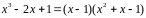 .
Значит,
.
Значит,
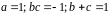 .
.
Тогда .
Задача
2.
В четырехмерном вещественном аффинном
пространстве
с некоторой декартовой системой координат
даны прямая
,
точка
и плоскость
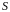 .
Прямая
.
Прямая
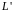 проходит через точку
и имеет общие точки с прямой
и плоскостью
.
Найдите расстояние между этими общими
точками.
проходит через точку
и имеет общие точки с прямой
и плоскостью
.
Найдите расстояние между этими общими
точками.
Вариант
1.
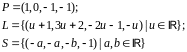 Вариант
2.
Вариант
2.
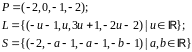 Вариант
3.
Вариант
3.
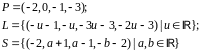
Вариант 4.
P=(1,3,2,3);
L={(2u1,
3u+5,u2,u2)|u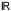 };
S={(b,a+3,a3,3)|a,b
}
};
S={(b,a+3,a3,3)|a,b
}
Вариант 5. P=(3,3,2,3); L={(u2,3u+5, 2u+2,u3)|u }; S={(3,a+3, b+1,a2)|a,b }
Решение.
Вариант
1.
Прямая
проходит через точку
с направляющим вектором
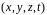 .
Поэтому
.
Поэтому
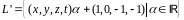 .
Чтобы эта прямая имела общие точки с
плоскостью
система
.
Чтобы эта прямая имела общие точки с
плоскостью
система
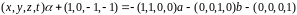
должна
быть совместна относительно переменных
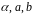 .
По теореме Кронеккера-Капелли должно
выполняться равенство:
.
По теореме Кронеккера-Капелли должно
выполняться равенство:
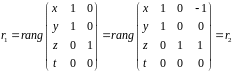
При
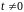
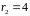 ,
,
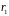 не может быть равен 4 (потому что столбцов
в матрице меньше 4). Следовательно,
система может быть совместной лишь при
не может быть равен 4 (потому что столбцов
в матрице меньше 4). Следовательно,
система может быть совместной лишь при
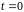 .
.
Для того, чтобы прямая имела общую точку с прямой , должна быть совместна система:
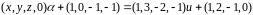
Совместность
этой системы равносильна тому, что
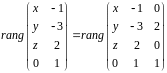 ,
первый из рангов, очевидно равен 2
(т.к вектор
ненулевой),
а второй равен двум в случае:
,
первый из рангов, очевидно равен 2
(т.к вектор
ненулевой),
а второй равен двум в случае:
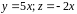 .
Таким образом, направляющим вектором
прямой
можно считать вектор
.
Таким образом, направляющим вектором
прямой
можно считать вектор
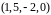 .
Получаем, что точка пересечения
и
равна
.
Получаем, что точка пересечения
и
равна
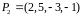 .
А общая точка
и
равна
.
А общая точка
и
равна
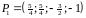 .
.
Расстояние
между точками
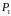 и
и
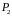 найти не трудно.
найти не трудно.
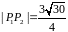
Варианты 2-5. Решение аналогично варианту 1. Ответ во всех вариантах
2008/2009 Учебный год. Все варианты.
Задача
1.
Ортогональная вещественная матрица
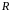 со свойством
со свойством
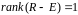 называется большим отражением.
а)
Разложите ортогональную матрицу
на произведение больших отражений;
б)
Какое наименьшее количество больших
отражений необходимо для разложения
матрицы
?
называется большим отражением.
а)
Разложите ортогональную матрицу
на произведение больших отражений;
б)
Какое наименьшее количество больших
отражений необходимо для разложения
матрицы
?
Вариант
1.
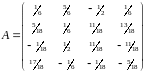
Вариант
2.
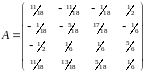
Вариант 3.
Вариант
4.
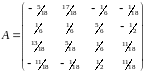
Вариант
5.
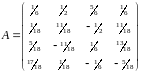
Вариант
6.
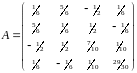
Решение
для варианта 1.
Давайте разберемся, что такое большое
отражение. Если
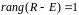 ,
значит 1 – собственное число матрицы
кратности
,
значит 1 – собственное число матрицы
кратности
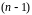 .
Остается только одно собственное число.
Оно не может быть комплексным (так как
комплексные числа появляются в паре со
своими сопряженными). Поэтому оставшееся
собственное число
.
.
Остается только одно собственное число.
Оно не может быть комплексным (так как
комплексные числа появляются в паре со
своими сопряженными). Поэтому оставшееся
собственное число
.
Поэтому произвольное большое отражение имеет вид
 ,
где
,
где
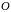 – некоторая ортогональная матрица.
– некоторая ортогональная матрица.
Большое отражение меняет направление последнего вектора в матрице , а остальные вектора из матрицы оставляет неизменными.
Перейдем непосредственно к задаче из варианта 1.
Проверим, является ли 1 собственным числом матрицы .
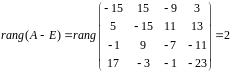
Таким
образом, 1 собственное число кратности
2. Канонический вид матрицы
будет
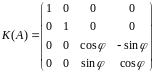 .
Поскольку у подобных матриц одинаковый
след, получаем
.
Поскольку у подобных матриц одинаковый
след, получаем
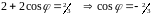 .
Поэтому матрица
соответствует повороту на угол
.
Поэтому матрица
соответствует повороту на угол
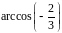 .
Из курса геометрии мы знаем, что поворот
есть композиция двух симметрий, оси
которых под углом
.
Из курса геометрии мы знаем, что поворот
есть композиция двух симметрий, оси
которых под углом
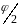 .
(Заметим, что
.
(Заметим, что
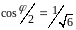 ;
косинус положителен, потому что можно
взять угол поворота меньше )
Найдем плоскость поворота
.
;
косинус положителен, потому что можно
взять угол поворота меньше )
Найдем плоскость поворота
.
Для
этого найдем множество
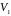 собственных векторов для 1. А плоскость
поворота будет ортогональна к
.
собственных векторов для 1. А плоскость
поворота будет ортогональна к
.
Поскольку собственные вектора для удовлетворяют системе уравнений
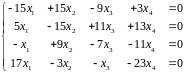
Поэтому
плоскость
натянута на вектора
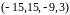 ,
,
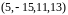 ,
,
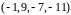 ,
,
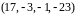 .
Вычеркнув лишнее, получаем, что
натянута на вектора
.
Вычеркнув лишнее, получаем, что
натянута на вектора
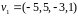 ,
,
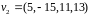 .
Надо взять любые два вектора из этой
плоскости под углом
.
Относительно них провести отражение и
получится как раз поворот, который
задает матрица
.
Один вектор пусть будет
.
Надо взять любые два вектора из этой
плоскости под углом
.
Относительно них провести отражение и
получится как раз поворот, который
задает матрица
.
Один вектор пусть будет
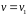 .
Значит, второй вектор будет
.
Значит, второй вектор будет
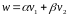 .
.
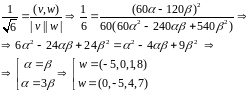
Надо
выбрать
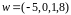 ,
чтобы косинус угла был положителен.
,
чтобы косинус угла был положителен.
Итак,
надо произвести две симметрии: одна
изменяет на противоположное направление
вектора
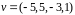 ;
вторая -- вектора
.
;
вторая -- вектора
.
Вектор дополняем до ортонормированного базиса пространства. Получаем, что большое отражение относительно вектора выглядит так:
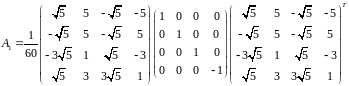
Произведя вычисления, получаем:
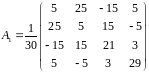
Вектор
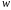 дополняем до ортонормированного базиса
всего пространства; получаем, что большое
отражение для вектора
выглядит так:
дополняем до ортонормированного базиса
всего пространства; получаем, что большое
отражение для вектора
выглядит так:
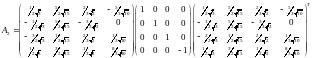
Произведя вычисления, получаем:
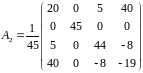
Заметим,
что
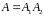 .
(Если необходимо, это можно проверить
прямыми вычислениями).
.
(Если необходимо, это можно проверить
прямыми вычислениями).
Ответ на вопрос б): очевидно, что минимальное количество равно 2, так как сама матрица большим отражением не является, а пример, когда исходная матрица раскладывается в произведение 2 больших отражений, мы привели.
Ответы.
Вариант
2.
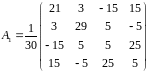
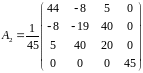 Вариант
3.
(см.вариант 2).
Вариант
4.
Вариант
3.
(см.вариант 2).
Вариант
4.
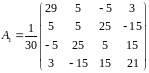
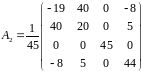 Вариант
5.
Вариант
5.

 Вариант
6:
исходная матрица уже большое отражение.
Вариант
6:
исходная матрица уже большое отражение.
Задача
2.
Обозначим через
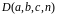 определитель
определитель
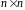 -матрицы,
на главной диагонали которой стоит
число
-матрицы,
на главной диагонали которой стоит
число
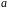 ,
на диагонали выше главной
число
,
на диагонали выше главной
число
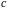 ,
а на диагонали ниже главной
число
.
Остальные места заняты нулями.
Вариант
1.
Найдите
,
а на диагонали ниже главной
число
.
Остальные места заняты нулями.
Вариант
1.
Найдите
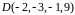 .
Вариант
2.
Найдите
.
Вариант
2.
Найдите
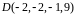 .
Вариант
3.
Найдите
.
Вариант
3.
Найдите
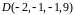 .
Вариант
4.
Найдите
.
Вариант
4.
Найдите
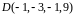 .
Вариант
5.
Найдите
.
Вариант
5.
Найдите
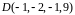 .
Вариант
6.
Найдите
.
Вариант
6.
Найдите
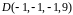 .
.
Решение
для варианта 1.
Разложим определитель
по первой строке, а потом один из
получившихся определителей – по первому
столбцу. Получим возвратную формулу:
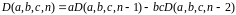 .
.
В
конкретном случае
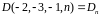 получаем
получаем
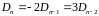 .
.
Вычисляем
первые члены:
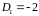 ,
,
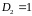 .
Подставляя эти значения в возвратную
форму, получаем
.
Подставляя эти значения в возвратную
форму, получаем
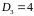 ;
;
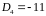 ;
;
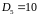 ;
;
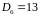 ;
;
 ;
;
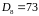 ;
;
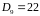 .
.
Ответы. Вариант 2 ответ 32; Вариант 3 ответ 10; Вариант 4 ответ 31; Вариант 5 ответ 11; Вариант 6 ответ 1.
