
- •Года: 04/05;05/06, 06/07; 07/08; 08/09; 09/10, 10/11.
- •2004/2005 Учебный год. Все варианты.
- •2005/2006 Учебный год. Вариант 1.
- •2005/2006 Учебный год. Вариант 2.
- •2005/2006 Учебный год. Вариант 3.
- •2005/2006 Учебный год. Вариант 4.
- •2005/2006 Учебный год. Вариант 5.
- •2006/2007 Учебный год. Вариант I-1.
- •2006/2007 Учебный год. Вариант I-2.
- •2006/2007 Учебный год. Вариант I-3.
- •2006/2007 Учебный год. Вариант I-4.
- •2006/2007 Учебный год. Вариант I-5.
- •2007/2008 Учебный год. Вариант 1.
- •2007/2008 Учебный год. Вариант 2.
- •2007/2008 Учебный год. Вариант 3.
- •2007/2008 Учебный год. Вариант 4.
- •2007/2008 Учебный год. Вариант 5.
- •2008/2009 Учебный год. Вариант II-1
- •2008/2009 Учебный год. Вариант II-2
- •2008/2009 Учебный год. Вариант II-3
- •2008/2009 Учебный год. Вариант II-4.
- •2008/2009 Учебный год. Вариант II-5.
- •2009/2010 Учебный год. Все варианты.
- •2008/2009 Учебный год. Все варианты.
2007/2008 Учебный год. Вариант 4.
Задача
1. Найти жорданову форму матрицы
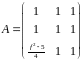 .
.
Решение. Найдем характеристический многочлен матрицы .
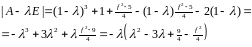
При
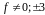 у матрицы ровно 3 различных собственных
числа:
у матрицы ровно 3 различных собственных
числа:
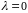 ,
,
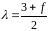 ,
,
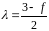 .
При
.
При
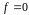 получаем собственное число 0 кратности
1 и собственное число 1,5 кратности 2.
Вычислим ранг матрицы
получаем собственное число 0 кратности
1 и собственное число 1,5 кратности 2.
Вычислим ранг матрицы
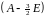
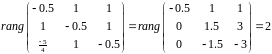
Значит, только одна жорданова клетка с собственным числом 1,5.
Рассмотрим
теперь
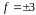 .
В этом случае получаем собственное
число 0 кратности 2 и собственное число
3 кратности 1. Заметим, что в этом случае
.
В этом случае получаем собственное
число 0 кратности 2 и собственное число
3 кратности 1. Заметим, что в этом случае
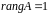 ,
поэтому 2 жордановых клетки с собственным
числом 0. Итак, ответ:
,
поэтому 2 жордановых клетки с собственным
числом 0. Итак, ответ:
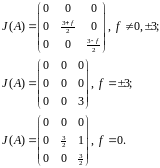
Задача
2.
Найдите расстояние между плоскостями
,
в четырехмерном аффинном пространстве,
если
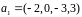
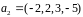 ,
,
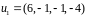 ,
,
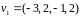 ,
,
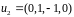 ,
,
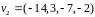 .
.
Решение. Задача аналогична задаче 2 из варианта 1, поэтому подробно объяснять решение не будем.
Найдем базис .

Заметим, что совпадает с из задачи первого варианта, так же совпадает. Т.е. решение далее совпадает. Ответ: расстояние между плоскостями
2007/2008 Учебный год. Вариант 5.
Задача
1.
Найдите жорданову форму матрицы
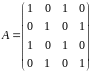
Решение. Вычислим характеристический многочлен матрицы .
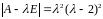 .
.
Заметим,
что
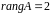 ;
;
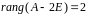 .
Следовательно,
.
Следовательно,
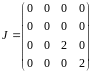
Задача
2.
Найдите
расстояние между плоскостями
,
в четырехмерном аффинном пространстве,
если
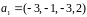 ,
,
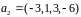 ,
,
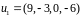 ,
,
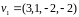 ,
,
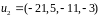 ,
,
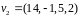 .
.
Решение. Задача аналогична задаче 2 из варианта 1, поэтому подробно объяснять решение не будем.
Найдем базис .

Заметим, что совпадает с из задачи первого варианта, так же совпадает. Т.е. решение далее совпадает. Ответ: расстояние между плоскостями
2008/2009 Учебный год. Вариант II-1
Задача
5.
Пусть даны многочлены
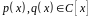 такие, что
такие, что
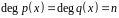 .
Доказать, что если
.
Доказать, что если
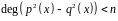 ,
то
,
то
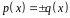 .
.
Решение.
Рассмотрим старший коэффициент
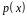 и старший коэффициент
и старший коэффициент
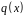 .
Если они равны, обозначим
.
Если они равны, обозначим
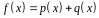 ,
,
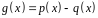 .
Если же они не равны, то наоборот
.
Если же они не равны, то наоборот
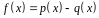 ,
,
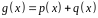 .
Заметим, что при введенных обозначениях,
при подсчете коэффициента при
.
Заметим, что при введенных обозначениях,
при подсчете коэффициента при
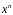 в многочлене
в многочлене
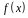 он сократиться не может и получается
не нулевым. Т.е.
он сократиться не может и получается
не нулевым. Т.е.
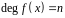 .
.
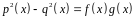 .
Причем степень
равна
.
Если
.
Причем степень
равна
.
Если
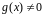 ,
то у него есть старший ненулевой член
,
то у него есть старший ненулевой член
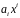 и тогда степень многочлена
и тогда степень многочлена
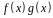 равна
равна
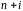 .
Но она по условию меньше
.
Противоречие. Значит, многочлен
.
Но она по условию меньше
.
Противоречие. Значит, многочлен
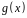 нулевой. А это означает, что либо
нулевой. А это означает, что либо
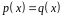 ,
либо
,
либо
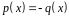 .
.
Задача
6.
Показать, что матрицы
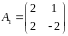 ,
,
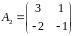 ,
,
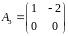 ,
,
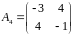 не образуют базис пространства
- матриц
не образуют базис пространства
- матриц
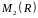 .
Найти размерность порождаемого ими
подпространства
.
Найти размерность порождаемого ими
подпространства
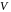 и пересечение
с подпространством верхнетреугольных
матриц
и пересечение
с подпространством верхнетреугольных
матриц
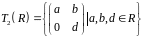 .
.
Решение.
Зафиксируем в качестве стандартного
базиса базис из матричных единиц
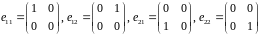 .
Разложим матрицы
.
Разложим матрицы
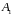 ,
,
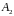 ,
,
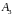 ,
,
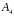 по этому базису и найдем методом Гаусса
базис их линейной оболочки.
по этому базису и найдем методом Гаусса
базис их линейной оболочки.

Таким
образом мы установили, что
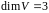 (и параллельно установили, что
,
,
,
не
является базисом всего пространства)
и нашли базис
:
(и параллельно установили, что
,
,
,
не
является базисом всего пространства)
и нашли базис
:
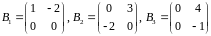 .
.
Заметим,
что в
входят не только верхнетреугольные
матрицы. Значит,
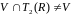 .
Значит,
.
Значит,
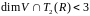 .
Заметим, что матрицы
.
Заметим, что матрицы
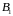 и
и
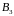 входят в
входят в
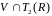 и линейно независимы. Значит, они и
являются базисом
.
Таким образом,
и линейно независимы. Значит, они и
являются базисом
.
Таким образом,
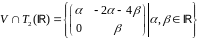 .
.
2008/2009 Учебный год. Вариант II-2
Задача 5. Даны два базиса векторного пространства
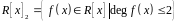 :
:
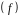
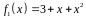 ,
,
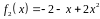 ,
,
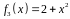 ;
;
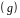
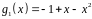 ,
,
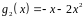 ,
,
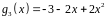 .
.
Найти
матрицу перехода от базиса
к базису
,
а также подсчитайте координаты вектора
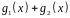 в базисе
.
в базисе
.
Решение.
Рассмотрим еще базис
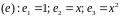 .
Легко написать матрицу перехода от
.
Легко написать матрицу перехода от
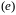 к
к
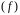 :
:
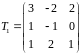 и матрицу перехода от базиса
к базису
и матрицу перехода от базиса
к базису
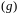 :
:
 .
Тогда матрица перехода от базиса
к базису
будет
.
Тогда матрица перехода от базиса
к базису
будет
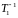 .
И матрица перехода от базиса
к базису
получится
.
И матрица перехода от базиса
к базису
получится
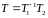 .
Чтобы найти координаты вектора
.
Чтобы найти координаты вектора
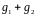 в базисе
надо вектор-столбец
в базисе
надо вектор-столбец
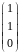 (координаты вектора
в
базисе
)
умножить на матрицу
(координаты вектора
в
базисе
)
умножить на матрицу
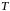 (слева).
(слева).
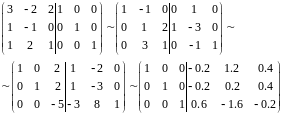
Значит,
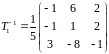 .
Тогда искомая матрица:
.
Тогда искомая матрица: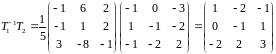
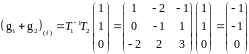
Задача
6.
Пусть
– матрица третьего порядка, все
собственные значения которой положительны.
Доказать, что
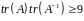 .
.
Решение.
Пусть матрица
 – жорданова форма матрицы
,
а
– жорданова форма матрицы
,
а
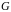 – жорданова форма матрицы
– жорданова форма матрицы
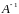 .
Тогда
.
Тогда
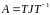 ,
,
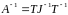 .
Следовательно, матрицы
.
Следовательно, матрицы
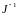 и
подобны и у них одинаковый набор
собственных чисел. Матрица
верхнетреугольная и значит,
тоже верхнетреугольная, причем на
диагонали стоят числа, обратные
соответствующим диагональным числам
матрицы
.
и
подобны и у них одинаковый набор
собственных чисел. Матрица
верхнетреугольная и значит,
тоже верхнетреугольная, причем на
диагонали стоят числа, обратные
соответствующим диагональным числам
матрицы
.
Следовательно,
если на диагонали у матрицы
стоят числа
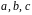 то на диагонали матрицы
стоят числа
то на диагонали матрицы
стоят числа
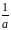 ,
,
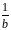 ,
,
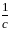 .
(Причем все эти числа положительны).
Поскольку следы подобных матриц
совпадают, получаем, что
.
(Причем все эти числа положительны).
Поскольку следы подобных матриц
совпадают, получаем, что
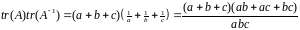
По
неравенству между средним арифметическим
и средним геометрическим для трех чисел,
получаем:
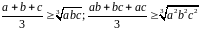 .
Перемножая эти два положительные
неравенства и получаем требуемое.
.
Перемножая эти два положительные
неравенства и получаем требуемое.
