
- •Года: 04/05;05/06, 06/07; 07/08; 08/09; 09/10, 10/11.
- •2004/2005 Учебный год. Все варианты.
- •2005/2006 Учебный год. Вариант 1.
- •2005/2006 Учебный год. Вариант 2.
- •2005/2006 Учебный год. Вариант 3.
- •2005/2006 Учебный год. Вариант 4.
- •2005/2006 Учебный год. Вариант 5.
- •2006/2007 Учебный год. Вариант I-1.
- •2006/2007 Учебный год. Вариант I-2.
- •2006/2007 Учебный год. Вариант I-3.
- •2006/2007 Учебный год. Вариант I-4.
- •2006/2007 Учебный год. Вариант I-5.
- •2007/2008 Учебный год. Вариант 1.
- •2007/2008 Учебный год. Вариант 2.
- •2007/2008 Учебный год. Вариант 3.
- •2007/2008 Учебный год. Вариант 4.
- •2007/2008 Учебный год. Вариант 5.
- •2008/2009 Учебный год. Вариант II-1
- •2008/2009 Учебный год. Вариант II-2
- •2008/2009 Учебный год. Вариант II-3
- •2008/2009 Учебный год. Вариант II-4.
- •2008/2009 Учебный год. Вариант II-5.
- •2009/2010 Учебный год. Все варианты.
- •2008/2009 Учебный год. Все варианты.
2006/2007 Учебный год. Вариант I-3.
Задача
1.
Найти наибольший общий делитель
многочленов
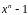 и
и
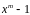 ,
,
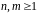 .
.
Решение.
Без ограничения общности можно считать,
что
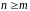 .
.
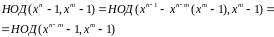 .
.
Теперь
умозрительно сделаем следующее. В левой
колонке будем проводить модифицированный
алгоритм Евклида для многочленов
и
.
1 шаг будет состоять в переходе как выше.
В конце-концов (т.к. суммарная степень
многочленов убывает, а НОД сохраняется)
мы придем к паре:
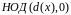 ,
многочлен
,
многочлен
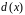 и будет искомым НОДом.
и будет искомым НОДом.
В
правой колонке будем проводить алгоритм
Евклида для чисел
,
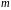 .
За один шаг переходим от пары
.
За один шаг переходим от пары
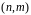 ,
где
к паре
,
где
к паре
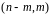 .
В конце этого алгоритма мы получим
.
В конце этого алгоритма мы получим
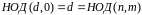 .
.
Заметим,
что на одинаковом шаге если в правой
колонке стоит
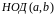 ,
то в левой стоит
,
то в левой стоит
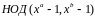 .
Значит, на последнем шаге получим как
раз
.
Значит, на последнем шаге получим как
раз
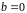 (и
(и
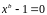 ),
a
),
a
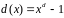 .
.
Ответ.
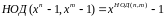 .
.
Задача
2.
Пусть
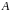
квадратная матрица
-го
порядка. Доказать, что если
квадратная матрица
-го
порядка. Доказать, что если
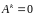 для некоторого
,
тогда
для некоторого
,
тогда
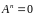 .
.
Решение.
Вероятнее всего, в задаче подразумевается,
что матрица рассматривается над полем
комплексных чисел (или над полем
вещественных чисел) и можно воспользоваться
теоремой о жордановой форме. Но мы в
решении даже не будем на это опираться
и рассмотрим матрицу над произвольным
полем
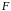 .
.
Если
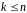 ,
то все очевидно
,
то все очевидно
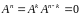 .
Предположим также, что
.
Предположим также, что
 при
при
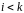 .
Рассмотрим действие матрицы
.
Рассмотрим действие матрицы
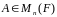 на векторном пространстве
на векторном пространстве
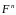 .
Понятно, что
.
Понятно, что
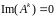 ,
поскольку матрица
,
поскольку матрица
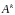 – нулевая.
– нулевая.
Понятно, что
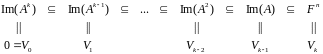 .
.
Потому
что
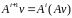 ,
т.е. любой вектор из
,
т.е. любой вектор из
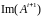 содержится в
содержится в
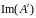 .
Заметим, что все подпространство
.
Заметим, что все подпространство
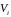 состоит из тех векторов, которые
зануляются за
состоит из тех векторов, которые
зануляются за
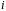 раз действием матрицей
.
Таким образом,
состоит из
раз действием матрицей
.
Таким образом,
состоит из
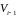 (т.е. тех векторов, которые зануляются
и за меньшее количество шагов) и тех
векторов, которые зануляются ровно за
раз.
(т.е. тех векторов, которые зануляются
и за меньшее количество шагов) и тех
векторов, которые зануляются ровно за
раз.
Заметим,
что если есть вектора, которые зануляются
ровно за
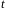 раз, обязательно есть вектора, которые
зануляются и ровно за
раз, обязательно есть вектора, которые
зануляются и ровно за
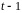 раз. Это вектора, которые зануляются за
раз, на которые подействовали матрицей
всего 1 раз.
раз. Это вектора, которые зануляются за
раз, на которые подействовали матрицей
всего 1 раз.
Мы
знаем, что
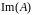 не может быть равно
.
Потому что иначе весь ряд был бы равен
и никогда бы не занулился. Значит,
существуют векторы, которые зануляются
ровно за
шагов (это вектора
не может быть равно
.
Потому что иначе весь ряд был бы равен
и никогда бы не занулился. Значит,
существуют векторы, которые зануляются
ровно за
шагов (это вектора
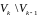 ).
Следовательно, существуют векторы,
которые зануляются ровно за
).
Следовательно, существуют векторы,
которые зануляются ровно за
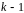 ,
,
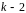 и т.д. шагов. Следовательно, на каждом
шаге включение строгое (равенство
и т.д. шагов. Следовательно, на каждом
шаге включение строгое (равенство
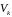 и
и
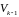 достигаться не может). Размерность
подпространства всегда меньше размерности
пространства (если подпространство не
равно всему пространству). Значит,
достигаться не может). Размерность
подпространства всегда меньше размерности
пространства (если подпространство не
равно всему пространству). Значит,
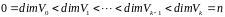 . Отсюда следует, что
.
Что и требовалось доказать.
. Отсюда следует, что
.
Что и требовалось доказать.
В предположении, что матрица рассматривается над полем действительных (или комплексных) чисел все проще. Матрица зануляется, значит она нильпотентная. Значит, ее жорданова форма состоит из жордановых клеток с нулем на диагонали. Самая максимальная жорданова клетка не может превышать размера матрицы. А нильпотентная матрица зануляется, если ее возвести в степень, равную размеру самой большой жордановой клетки.
2006/2007 Учебный год. Вариант I-4.
Задача
1.
Найти жорданову форму матрицы
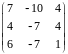 .
.
Решение. Вычисляем собственные числа матрицы как корни характеристического многочлена:

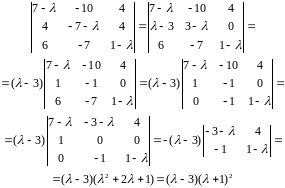
Таким
образом, собственные числа
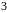 и
.
Причем, с числом 3 – одна жорданова
клетка размера
и
.
Причем, с числом 3 – одна жорданова
клетка размера
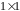 .
С числом
может быть либо 2 клетки
,
либо 1 клетка
.
С числом
может быть либо 2 клетки
,
либо 1 клетка
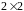 .
Чтобы различить эти случаи, вычислим
.
Чтобы различить эти случаи, вычислим
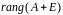 .
.
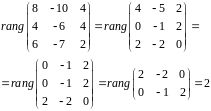
Поскольку
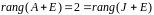 (здесь
(здесь
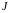 – жорданова форма матрицы
,
а ранги подобных матриц совпадают).
Следовательно,
– жорданова форма матрицы
,
а ранги подобных матриц совпадают).
Следовательно,
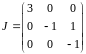
Задача
2.
Доказать, что если оператор
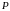 векторного пространства
векторного пространства
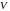 имеет в некотором базисе диагональную
матрицу, то его ограничение на любое
инвариантное подпространство
имеет в некотором базисе диагональную
матрицу, то его ограничение на любое
инвариантное подпространство
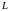 тоже имеет диагональную матрицу в
некотором базисе
.
тоже имеет диагональную матрицу в
некотором базисе
.
Решение.
– инвариантное подпространство
пространства
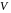 .
Значит, можно рассматривать оператор
.
Значит, можно рассматривать оператор
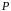 ,
действующий только на
.
В частности, можно найти жорданову форму
оператора
.
Предположим, что не все жордановы клетки
размером
,
есть и большие. Т.е. существует число
,
действующий только на
.
В частности, можно найти жорданову форму
оператора
.
Предположим, что не все жордановы клетки
размером
,
есть и большие. Т.е. существует число
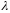 и вектора
и вектора
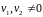 из
такие что
из
такие что
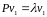 ;
;
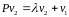 .
(Вектора
.
(Вектора
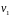 и
и
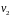 можно выбрать из жорданова базиса
оператора
в пространстве
).
можно выбрать из жорданова базиса
оператора
в пространстве
).
Теперь снова рассмотрим оператор в пространстве . Поскольку , - собственное число этого оператора. Причем вектор – собственный вектор оператора , а вектор – из корневого подпространства, соответствующего собственному числу . Но мы знаем, что жорданова форма оператора диагональна и следовательно все корневые пространства глубины 1, т.е. в корневых пространствах только собственные вектора, а векторов высоты 2 быть не может. Противоречие.
