Года: 04/05;05/06, 06/07; 07/08; 08/09; 09/10, 10/11.
2004/2005 Учебный год. Все варианты.
Задача 1. (Вариант I-1.) Найти общее решение системы уравнений
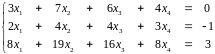
Решение. Перепишем систему в матричном виде; будем действовать методом Гаусса:
Отсюда
получаем:
.
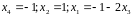Варианты I-2, I-3, I-4 решаются абсолютно аналогично. Так что приведем толкьо ответы:
Вариант
I-2.
.
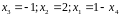Вариант
I-3.
.
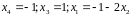Вариант
I-4.
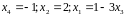x4=1;.
Задача
2.
(Вариант I-1). Найти все значения параметра
a,
при которых число
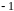является корнем кратности два многочлена
.
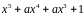Решение.
Заметим, что
.
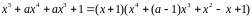Чтобы
была корнем кратности 2 необходимо,
чтобы
была корнем многочлена
.
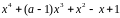Т.е.
.
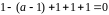Получаем,
.
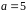Надо проверить, не получился ли при
корень
кратности больше, чем 2.
.
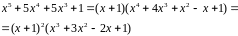Число
не является корнем многочлена
,
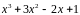значит,
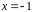является корнем кратности 2 многочлена
только при
.
Вариант
I-2.
.
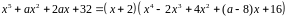Значит,
.
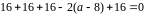Получаем
.
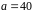Проверяем, что при
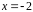является корнем кратности 2 (а не выше).
Вариант
I-3.
.
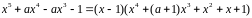Получаем
.
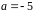Проверяем, что
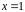не является корнем большей кратности,
чем 2.
Объясним еще другое решение той же задачи на примере варианта I-4.
Задача
2.
Найти все значения параметра a,
при которых число 2
является корнем кратности два многочлена
.
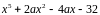Решение.
Заметим, что
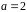является корнем многочлена
.
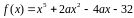Для того, чтобы корень являлся корнем
кратности 2 необходимо и достаточно,
чтобы он являлся корнем производной
кратности 1. Т.е. чтобы он являлся корнем
производной, но при этом не являлся
корнем второй производной.
Ищем
производную:
.
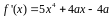Из условия,
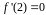получаем
.
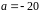Проверяем,
что корень
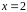ровно кратности 2 (а не выше). Для этого
вычисляем
.
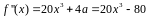не является корнем этого многочлена.
Поэтому кратность корня именно 2.
2005/2006 Учебный год. Вариант 1.
Задача
1.
При каком
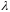пространства
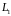и
,
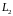натянутые на вектора
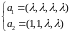и
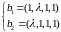
соответственно, имеют ненулевое пересечение?
Решение.
Рассмотрим
.
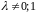В этом случае
и
двумерны и они пересекаются по нулю
тогда и только тогда, когда их объединение
четырехмерно, т.е. система векторов
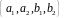линейно независима.
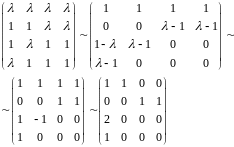
Т.е.
.
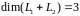Поэтому пересечение ненулевое.
Рассмотрим
.
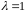Тогда
.
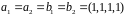Поэтому пересечение снова ненулевое.
Рассмотрим
.
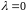Тогда
;
.
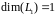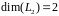А
.
Поэтому
.
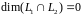Ответ:
при
.
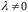Задача 2. Найти жорданову форму матрицы
.
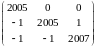Решение.
Найдем собственные числа из условия
.
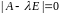Получаем:
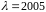кратности 1;
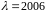кратности 2. Вычислим ранг матрицы
.
.
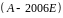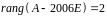Поэтому жорданова форма получается:
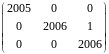
2005/2006 Учебный год. Вариант 2.
Задача
1.
Система
ненулевых векторов
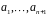имеет ранг
.
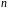Докажите, что она имеет
как
минимум два различных базиса.
Решение.
Заметим, что система
линейно зависима, а значит существует
нетривиальная линейная комбинация
.
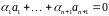Поскольку система состоит из ненулевых
векторов, значит среди
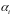есть минимум два ненулевых числа. Без
потери общности можно считать, что это
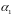и
.
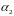Таким образом, вектор
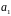выражается через
.
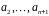Поскольку ранг системы n,
получаем что
– базис системы. Аналогично, вектор
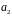выражается через остальные и поэтому
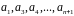– тоже базис системы. Что и требовалось
доказать.
Задача 2. Найти жорданову форму матрицы
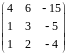
Решение.
Собственные числа этой матрицы:
кратности 3. Вычислим ранг матрицы
.
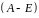Поскольку
,
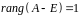получаем, что жорданова форма
.