Санкт-Петербургский Государственный Политехнический университет

Автор

Рыжаков Игорь Юрьевич

Неопределенный и определенный

интеграл

Методичка

Оглавление

Стр.

§1. Неопределённый интеграл

1. Первообразная функция …………………………………………………….. 3

2. Неопределённый интеграл …………………………………………………. 3

3. Теоремы, облегчающие отыскание неопределённых интегралов ……….. 5

4. Метод подстановки ………………………………………………………….. 7

5. Интегрирование рациональных функций …………………………………. 9

6. Интегрирование тригонометрических функций ………………………….. 12

7. Интегрирование дифференциального бинома ……………………………. 14

§2. Определенный интеграл

1. Площадь плоской фигуры …………………………………………………. 16

2. Точные грани ограниченной функции …………………………………… 17

3. Положительная и отрицательная части функции ……………………….. 19

4. Интегральные суммы ……………………………………………………… 20

5. Геометрический смысл интегральных сумм неотрицательной функции . 21

6. Свойства интегральных сумм …………………………………………….. 22

7. Интегрируемые функции …………………………………………………. 23

8. Определенный интеграл ………………………………………………….. 27

9. Свойства определенного интеграла, выражаемые равенствами ………. 28

10. Свойства определенного интеграла, выражаемые неравенствами ……. 30

11. Теоремы о среднем для определенного интеграла …………………….. 31

12. Определенный интеграл с переменным верхним пределом …………... 33

13. Способы вычисления определенных интегралов ……………………… 34

§3. Несобственные интегралы

1. Несобственный интеграл по [a,b) ………………………………………. 36

2. Несобственный интеграл по (a,b] ……………………………………… 41

3. Несобственный интеграл по (a,b) ……………………………………… 44

4. Замена переменной в несобственном интеграле ……………………… 46

5. Главное значение несобственного интеграла …………………………. 49

6. Несобственный интеграл от функции, имеющей особые точки

внутри промежутка интегрирования ………………………………….. 51

§1. Неопределённый интеграл

1. 1. Первообразная функция

Пусть на некотором промежутке Х = , где а<b, ограниченном или неограни- ченном, определены две функции и F, причём F дифференцируема на X.

Определение. Функцию F назовём первообразной функцией (или, короче, перво- образной) для функции на промежутке X, если (если , то ; если , то ).

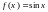Пример 1. Пусть Х= , , . Так как на , то есть первообразная для на . Функция является первообразной для на : .

Теорема 1. ( Об общей форме первообразных) Пусть F и Ф – две функции, диффе- ренцируемые на X , причём F есть первообразная для на X: . Для того, чтобы  также была первообразной для на X, необходимо и достаточно, чтобы Ф можно было представить в виде суммы функции F и некоторой константы С, : .

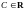Необходимость. Пусть  – первообразная функции на Х: . Положим . Тогда . В силу критерия постоянства функции на промежутке (глава 2, п.3.1) на X, где , т.е., 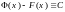на X. Отсюда: .

Достаточность очевидна: если , то .

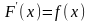Следствие. Пусть F есть первообразная для на X. Тогда совокупность , где С принимает всевозможные вещественные значения, есть множество всех первообразных функции на X.

Справедливость утверждения следствия очевидна ввиду теоремы 1. Поясним, что выражение F(x)+C есть сумма двух функций: функции F(x) и функции, тождественно на Х равной С.