
- •230105 (2203) Программное обеспечение вычислительной техники и автоматизированных систем
- •Содержание
- •Тема 1.2 симплекс-метод.
- •Тема 1.3 прямая и двойственная задачи лп. Двойственный симплекс-метод.
- •Тема 1.4 транспортная задача.
- •Раздел 2. Нелинейное программирование.
- •Тема 2.1 нелинейное программирование.
- •Тема 2.2 градиентные методы.
- •Раздел 3. Сетевое программирование.
- •Тема 3.1 алгоритмы на сетях.
- •Тема 3.2 максимальный поток.
- •Раздел 4. Динамическое программирование.
- •Тема 4.1 модели динамического программирования.
- •Распределение капитальных вложений
- •Динамическая задача управления запасами
- •Раздел 5. Теория игр.
- •Тема 5.1 основные понятия теории игр.
- •Формализация игры. Матрица игры
- •Нижняя и верхняя цена игры
- •1. Цена игры I равна цене игры g;
- •Смешанные стратегии
- •Решение игр вида 2хn и mх2
- •1. Антагонистические игры
- •Задача принятия решений в условиях неопределенности
- •Принятие решений в условиях частичной неопределенности
Динамическая задача управления запасами
Задача управления запасами – это задача о поддержании баланса производства и сбыта продукции предприятия, минимизирующего расходы предприятия на производство и хранение продукции.
Предположим, что предприятие, производящее партиями некоторую продукцию, получило заказы на n месяцев. Размеры заказов значительно меняются от месяца к месяцу, поэтому иногда лучше выполнять заказы сразу нескольких месяцев, а затем хранить готовую продукцию, пока она не потребуется, чем выполнять заказ именно в тот месяц, когда этот заказ должен быть отправлен. Поэтому необходимо составить план производства на эти n месяцев с учетом затрат на производство и хранение изделий.
Примем следующие обозначения:
-
Номер месяца (j=1,2,…,n)
Число изделий, производимых в j-ом месяце

Величина запаса к началу j-го месяца

Число изделий, которые должны быть отгружены в j-ом месяце

Затраты на хранение и производство изделий в j-ом месяце
Тогда,
задача состоит в том, чтобы найти план
производства
 компоненты которого удовлетворяют
условиям материального баланса:
компоненты которого удовлетворяют
условиям материального баланса:
 ,
где
,
где
и минимизируют суммарные затраты за весь планируемый период:

причем
по смыслу задачи
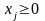 ,
,
 ,
при
,
при
Т.к.
объем произведенной продукции
на этапе j
может быть настолько велик, что запас
 может удовлетворить спрос всех последующих
этапов и при этом не имеет смысла иметь
величину запаса
больше суммарного спроса на всех
последующих этапах, то переменная
должна удовлетворять ограничениям:
может удовлетворить спрос всех последующих
этапов и при этом не имеет смысла иметь
величину запаса
больше суммарного спроса на всех
последующих этапах, то переменная
должна удовлетворять ограничениям:

Полученную задачу можно решить методом динамического программирования, для чего необходимо определить параметр состояния и функцию состояния :
-
Наличный запас продукции в конце k-го месяца (
 )
)Минимальные затраты за первые месяцев:

Тогда,
минимальные затраты за один первый
месяц ( ):
):

Следовательно, минимальные затраты при :
 ,
где
,
где

Если при этом функция затрат на хранение и производство изделий в j-ом месяце имеет вид:
 ,
где
,
где
-
 ,
при
,
при
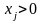 и
и
 ,
при
,
при


Затраты на оформление заказа (переналадку оборудования) в j-ом месяце
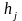
Затраты на хранение единицы продукции, переходящей из j‑го месяца в месяц j+1

Затраты на производство (закупку) единиц продукции в j‑ом месяце
то минимальные затраты за один первый месяц ( ):

если ввести обозначение:
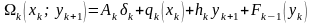
то следовательно, минимальные затраты при :
 ,
где
,
где
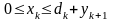
Допустим,
что предприятие заключило договора на
поставку своей продукции на три месяца.
Исходные данные приведены в таблице 9.
При этом исходный запас товара на складе
составляет две единицы, т.е
 .
.
Таблица 9. |
|||
Период k |
1 |
2 |
3 |
Спрос ( ) |
3 |
2 |
3 |
Затраты на оформление заказа ( ) |
4 |
2 |
3 |
Затраты на хранение единицы запаса ( ) |
1 |
1 |
1 |
Предполагается, что затраты на приобретение продукции составляют 5 руб. за каждую единицу для первых трех единиц и 7 руб. за каждую дополнительную единицу, т.е.

Положим , тогда:

Тогда,
т.к. параметр состояния
 может принимать значения на отрезке:
может принимать значения на отрезке:

т.е.
 ,
при этом каждому значению параметра
состояния отвечает определенная область
изменения переменной
:
,
при этом каждому значению параметра
состояния отвечает определенная область
изменения переменной
:

Однако
на первом этапе объем производства не
может быть меньше одной единицы, т.к.
спрос
 ,
а исходный запас
,
при этом из балансового уравнения
следует, что объем производства связан
с параметром состояния
соотношением:
,
а исходный запас
,
при этом из балансового уравнения
следует, что объем производства связан
с параметром состояния
соотношением:

т.е.
каждому значению
 отвечает единственное значение
,
поэтому:
отвечает единственное значение
,
поэтому:
 ,
тогда:
,
тогда:
|
|
|
Значения
функции состояния
 приведены в таблице 10.:
приведены в таблице 10.:
Таблица 10. |
||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
|
9 |
15 |
21 |
29 |
37 |
45 |
|
1 |
2 |
3 |
4 |
5 |
6 |
Положим
 ,
тогда:
,
тогда:
 ,
где:
,
где:

Здесь минимум берется по переменной , которая может изменяться в пределах:

где
верхняя граница зависит от параметра
состояния
 ,
который принимает значения на отрезке:
,
который принимает значения на отрезке:

т.е.
 ,
при этом из балансового уравнения
следует, что остаток товара на начало
второго месяца
связан с объемом производства
и с параметром состояния
,
при этом из балансового уравнения
следует, что остаток товара на начало
второго месяца
связан с объемом производства
и с параметром состояния
 соотношением:
соотношением:

Тогда:
( |
|
|
|
Наименьшие
из полученных значений
 ,
есть
,
есть
 ,
т.е.:
,
т.е.:

причем минимум достигается при и , т.е.:
 и
и

эти значения указываем в результирующей таблице 11.
Аналогично:
( |
|
|
|
( |
|
|
|
( |
|
|
|
Таким образом:
Таблица 11. |
|||||
|
0 |
1 |
2 |
3 |
|
|
21 |
27 |
34 |
41 |
|
|
0 |
2 |
3 |
3 |
3 |
Теперь
положим, что
 ,
тогда:
,
тогда:
 ,
где:
,
где:

Если
оставлять продукцию к концу третьего
периода не нужно, тогда параметр состояния
принимает единственное значение
 ,
следовательно, переменная
может изменяться в пределах:
,
следовательно, переменная
может изменяться в пределах:

а
из балансового уравнения следует, что
остаток товара на начало третьего месяца
 связан с объемом производства соотношением:
связан с объемом производства соотношением:

Тогда:
( |
|
|
|
Следовательно, получаем:

причем минимум достигается при , т.е.:

Таким образом, получили минимальные общие затраты на производство и хранение продукции и последнюю компоненту оптимального решения:

Для нахождения остальных компонент оптимального решения, необходимо воспользоваться обычными правилами динамического программирования.
Тогда т.к.
 ,
то
,
то
 ,
откуда
,
следовательно, из таблицы 11.:
,
откуда
,
следовательно, из таблицы 11.:
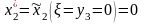 или
или

Аналогично
т.к.
 ,
то
,
то
 или
или
 ,
откуда
или
,
следовательно, из таблицы 10.:
,
откуда
или
,
следовательно, из таблицы 10.:
 или
или

Следовательно, получен оптимальный план производства, который имеет два варианта:
|
|
при этом, каждый вариант оптимального плана производства обеспечивает минимальные общие затраты на производство и хранение продукции в размере 39 денежных единиц.
Элементы модели динамического программирования. Задача распределения капиталовложений
Совет директоров фирмы изучает предложения по наращиванию производственных мощностей на трех принадлежащих фирме предприятиях. Для расширения всех трех предприятий фирма выделяет средства в объеме 5 млн. долл. Каждое предприятие представляет на рассмотрение проекты, которые характеризуются величинами (в миллионах долларов) суммарных затрат (с) и доходов (R), связанных с реализацией каждого из проектов. Соответствующие данные приведены в табл.. 9.1, в которую включены также проекты с нулевыми затратами. Это позволяет учесть возможность отказа от расширения какого-либо предприятия. Цель фирмы состоит в получении максимального дохода от инвестиций в объеме 5 млн. долл
Таблица 9.1

Прямой и, по-видимому, чрезмерно упрощенный способ решения сформулированной задачи заключается в использовании процедуры полного перебора. Задача имеет 3x4x2=24 возможных решения, причем некоторые из них не являются допустимыми, так как предполагают ассигнование свыше 5 млн. долл. В процессе полного перебора вычисляются суммарные затраты, ассоциированные с каждым из 24 возможных решений. Если величина затрат не превышает объема авансированных средств, следует вычислить соответствующий суммарный доход. Оптимальным будет допустимое решение, _обеспечивающее максимум суммарного дохода. Например, затраты на реализацию проектов 2, 3 и 1 для предприятий 1, 2 и 3 составляют 4 млн. долл. (<5), а суммарный доход равен 14 млн. долл. С другой стороны, набор проектов 3, 4 и 2 не является допустимым, так как объем затрат в этом случае равен 7 млн. долл.
Отметим следующие недостатки процедуры полного перебора.
Каждая комбинация проектов определяет некоторое решение задачи в целом, откуда следует, что перебор всех возможных комбинаций в задачах средней и большой размерности может быть связан с чрезмерно большим объемом вычислении.
Отсутствует априорная информация о решениях, которые не являются допустимыми, что снижает эффективность вычислительной схемы полного перебора.
Информация, полученная в результате анализа некоторых комбинаций проектов, в дальнейшем не используется для выявления и исключения неоптимальных комбинаций.
Применение методов ДП позволяет устранить все перечисленные недостатки. Ниже будет рассмотрена сетевая модель, отвечающая условиям сформулированной задачи, и показано, что нахождение самого длинного пути (максимального дохода) между крайними узлами сети приводит к получению оптимального решения исходной задачи. Вычисления на сетях характерны для ДП. Можно ожидать, что исследование сетевой модели позволит лучше уяснить специфику рекуррентной вычислительной схемы ДП.
Сетевая модель
Для построения сети следует определить этапы решения задачи. В рассмотренном примере каждому из предприятий ставится в соответствие некоторый этап, поскольку требуется выбрать оптимальный проект для каждого предприятия. Известно, что этапы связаны между собой посредством ограничения на суммарный объем капиталовложений. При построении модели необходимо учесть эту связь таким образом, чтобы получить возможность по отдельности решать подзадачи, соответствующие каждому этапу, не нарушая при этом условия допустимости. Введем следующие определения:
х1=объем капиталовложений, распределенных на этапе 1; ха=объем капиталовложений, распределенных на этапах 1 и 2; х3=объем капиталовложений, распределенных на этапах 1, 2, 3.
Далее будет показано, как можно использовать эти определения для разбиения исходной задачи на подзадачи и построения сетевой модели.
Заметим, что конкретные значения хг и х% заранее не известны, однако мы знаем, что эти значения лежат в интервале между 0 и 5. Так как затраты на реализацию каждого из проектов выражаются целыми числами, значения хг и х2 могут быть равны 0, 1, 2, 3, 4 и 5. С другой стороны, значение переменной х3, которая выражает объем капиталовложений, распределенных на всех трех этапах, равно 5.
Рис. 9.1 служит иллюстрацией сетевой модели для рассматриваемой задачи. Каждому возможному значению хь х2 и х3 поставлен в соответствие узел, ассоциированный с одним из этапов /=1, /=2 и /=3. Начальный этап /=0 введен в рассмотрение для удобства вычислений. Длины дуг, соединяющих узлы на некотором этапе с узлами на последующем этапе, численно равны доходам от реализации наилучшего допустимого проекта. Рассмотрим дуги, соединяющие узел U на этапе/=0 с узлами 0, 1, 2, 3, 4, 5 на этапе /= 1. Дуга (О, 0) (соединяющая узлы 0 на этапе /=0 и 0 на этапе /= 1) соответствует случаю, когда средства на этапе 1 не выделяются. Допустимым

здесь является проект 1 с Л?1=0, и дуге (0, 0) приписывается длина Ri (О, 0)=0. С другой стороны, для дуги (0, 1) допустимыми оказываются проекты 1 и 2, что предопределяет выбор проекта 2 с более высоким уровнем дохода /=5; дуге (0, I) приписывается длина 5. По тем же самым причинам дуге (0, 2) приписывается длина 6, поскольку здесь все три проекта являются допустимыми, а проекту 3 соответствует самый высокий уровень дохода /=6. Значения i=3, 4 и 5 соответствуют «избыточным» вариантам, для которых в лучшем случае =6.
Если внимательно изучить построенную сеть, то нетрудно" заметить, что некоторые дуги можно отбросить как заведомо неоптимальные. Например, можно исключить дугу (0, 1) между этапами /=1 и /=2, так как ассигнование =l млн. долл. на этапе 2 не приносит никакого дохода, поскольку эта сумма не является достаточной для реализации проекта 2. Исключение неоптимальных дуг значительно уменьшает объем необходимых вычислений. Однако чтобы сделать изложение материала более доходчивым, мы не будем рассматривать процедуры такого рода. Тем не менее, если у вас появился интерес к проблеме идентификации неоптимальных дуг, рекомендуем обратиться к следующему упражнению.
Упражнение 9.1.1. Выявите все заведомо неоптимальные дуги сети, изображенной на рис. 9.1.
Ответ. Все перечисленные ниже дуги заведомо не являются оптимальными, так как соответствуют вариантам с элементами неокупаемых затрат. Дуги между этапами /—0 и /=1: (0, 3), (0, 4) и (0, 5). Дуги между этапами /—1 и /=2: (0, 1), (0, 5), (1, 2), (2, 3), (3, 4), (4, 5). Дуги между этапами /=2 и /=3: (0, 5), (1, 5), (2, 5) и (3, 5).
После того как сеть построена, найдем самый длинный путь от узла 0 на этапе /=0 до узла 5 на этапе /=3. Метод решения этой задачи аналогичен методу нахождения кратчайшего маршрута. Представляется целесообразным описать метод поиска самого длинного пути подробно, так как он тесно связан с вычислительной схемой динамического программирования.
Обозначим через fj(Xj) величину самого длинного пути, ведущего в узел xj на этапе /. Поскольку /—О — исходный этап, /0(0)=0. Далее вычисления производятся поэтапно.
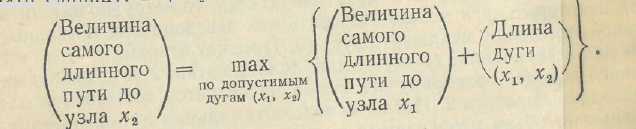
Ниже приводятся результаты вычислений по данной формуле. (Советуем обратиться к рис. 9.1 и проследить за ходом вычислений.)
f2(1)=max{0+0; 5+0}=5,
f2(2)=max{0+8; 5+0; 6+0}=8,
f2(3)=max
{0+9; 5+8; 6+0; 6+0} = 13, ,

fa(4)max (0+12; 5+9; 6+8; 6+0; 6+0} = 14,
f2(5)=max J0+12; 5+12; 6+9; 6+8; 6+0; 6+0} = 17. Полученные результаты представлены на рис. 9.2, б, на котором показаны дуги, соответствующие вычисленным значениям f2. Как и ранее, числа в круглых скобках обозначают номера проектов, ассоциированных с конкретными дугами.
В результате вычислений находим (см. рис. 9.1) f3(5)=max {0+3;5+3;8+3;13+3;14+3;17+0}=17.
Всего имеется три различных решения, которые приводятся в следующей таблице:

Отметим, что всем трем решениям соответствует один и тот же уровень дохода, а именно 17млн. долл.






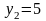






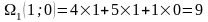



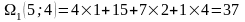





 )
)





 *
*
 *
*
 )
)







 *
*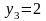
 )
)

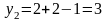






 *
*

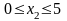 )
)



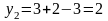


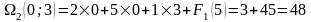


 *
*




 )
)










 *
*
