
- •1. Практична робота № 1
- •Тема: Прості обчислення з використанням програми Mathcad
- •Вказівки до виконання роботи:
- •Практична робота №2, 3
- •Побудова функції, заданої в аналітичному виді.
- •Варіанти індивідуальних завдань.
- •Завдання №2.
- •Завдання №3
- •Практична робота № 5, 6 Тема: Розв’язання системи лінійних та нелінійних рівнянь.
- •Теоретичні відомості.
- •Варіанти завдань №1.
- •Тема : Рішення нелінійних рівнянь у програмі Mathcad.
- •Варіанти завдань №2.
- •Варіанти завданнь №3.
- •Практична робота № 7
- •Завдання №1.
- •Тема1: Рішення задачі одновимірної оптимізації.
- •Варіанти завдання 1.
- •Тема2: Рішення задачі багатовимірної оптимізації.
- •Ознакомтесь з короткими теоретичними відомостями по побудові об'ємних графіків. Побудова об'ємних графіків поверхонь
- •Форматування тривимірних графіків
- •Варіанти завдання 2.
- •Контрольні питання:
Практичні роботи
з дисципліни
«Інформатика»
напрям підготовки 6.050503 Машинобудування
2 семестр
Зміст
1. Практична робота № 1
Тема: Прості обчислення з використанням програми Mathcad 3
2. Практична робота №2, 3
Тема: Організація циклічних обчислень за допомогою ранжованої змінної 5
3. Практична робота №4
Тема: Побудова двомірних графіків в координатних осях X-Y 13
4. Практична робота № 5, 6
Тема: Розв’язання системи лінійних та нелінійних рівнянь 18
5. Практична робота № 7
Тема: Розв’язання задачі оптимізації в середовищі Mathcad 24
Практична робота № 1
Тема: Прості обчислення з використанням програми Mathcad
Мета роботи
Освоїти основні прийоми роботи в програмі MATHCAD, навчитися використовувати набірні панелі для обчислень і обробки векторів і матриць.
Вказівки до виконання роботи:
Завантажити програму Mathcad за допомогою ярлика.
Виконати Завдання 1 – Завдання 6, використовуючи теоретичні вказівки.
Документ оформити текстовими коментарями, що пояснюють: номер практичної роботи, тему, мету і послідовність виконання роботи.
Зберегти документ у файлі під ім'ям Практична робота №1_Прізвище в особистій теці.
Варіанти Завдання 1.
Обчислити значення формули, заздалегідь визначивши змінні довільними значеннями.
Привласнення реалізувати за допомогою кнопки : = (Привласнити).
1.
![]() 11.
11.
![]()
2.
![]() 12.
12.

3.
 13.
13.
![]()
4.
![]() 14.
14.

5.![]() 15.
15.
![]()
6.
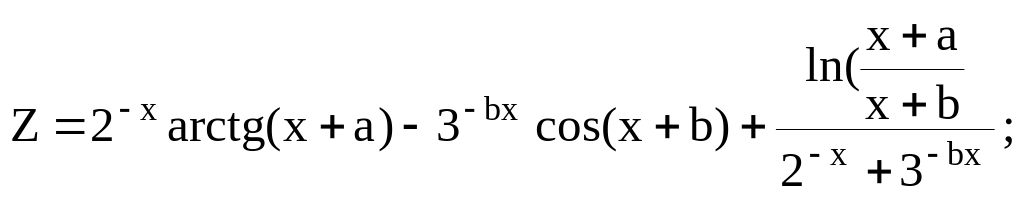 16.
16.
![]()
7.
![]() 17.
17.

8.
![]() 18.
18.
![]()
9.
![]() 19.
19.
![]()
10.
![]() 20.
20.
![]()
Завдання 2.
а). Обчислити скалярний добуток двох векторів, заданих самостійно.
би). Створити дві матриці і обчислити їх добуток.
Завдання 3.
Створити довільну матрицю А.
Визначити чи має матриця А зворотну, і якщо має, то обчислити її.
Завдання 4.
а).Створити довільний вектор В. Вичисліть суму першого і останнього елементів вектора.
би). Створити матрицю А. Вичисліть суму першого елементу першого рядка і останнього елементу передостаннього стовпця.
Завдання 5.
а).Створити довільний вектор В. Вичисліть суму всіх елементів вектора.
би). Створити матрицю А. Вичисліть суму елементів першого стовпця матриці. Обчислити суму елементів другого рядка матриці.
Завдання 6.
Обчислити суму елементів другого стовпця матриці А:
 .
.
Обчислити суму елементів 3-го рядка матриці А.
Переставити рядки матриці А так, щоб елементи 3-го стовпця розташовувалися в зростаючому порядку.
Обчислити суму елементів, розташованих на перетині стовпців 3,4 і рядків 4,6 матриць А.
Визначити суму максимального і мінімального елементів матриці А.
Визначити середнє значення елементів 5-го стовпця матриці А.
Знайти суму двох матриць С і D, де С – матриця, рядки якої є першими п'ять рядків матриці А; D – одинична матриця.
Визначити кількість рядків матриці, які не містять нульових елементів.
![]()

Контрольні питання:
Для чого використовується панель Математика?
Які засоби створення і обробки векторів і матриць ви знаєте?
Яке призначення індексованою змінною? Як вона створюється?
Які стандартні функції для обробки векторів і матриць ви знаєте?
Практична робота №2, 3
Тема: Організація циклічних обчислень за допомогою ранжируваної змінної.
Мета роботи
Освоїти прийоми роботи з ранжованою змінною.
Вказівки до виконання роботи:
У завданнях 1 і 4 при створенні векторів опишіть ранжовану зміну і, значення якої використовуватиметься як номер елементу вектора, тобто вона повинна набувати цілих значень. А для створення значення відповідного елементу вектора підберіть вираз, який повинен залежати від і і набувати необхідного значення.
У 2-му завданні використовуйте дві ранжовані змінні для створення елементів матриці, значення яких проаналізуйте і підберіть, якщо потрібний, необхідний вираз.
У 3-му завданні при необхідності використовуйте дві ранжовані змінні. Підберіть для них значення, проаналізувавши закономірності зміни значень індексів вибираних елементів матриці.
Варіанти завдань:
№ варіанту
|
Завдання
|
1 |
4,5; 5; 5,5; 6; 6,5; 7; 7,5.
Значення функції зберегти у векторі F.
|
2 |
0,5; 1,5; 2,5; 3,5; 4,5.
.
Значення функції зберегти у векторі F. |
3 |
1; 1,5; 2; 2,5; 3; 3,5.
.
Значення функції зберегти у векторі F.
|
4 |
0,5i; 1,5i; 2,5i; 3,5i; 4,5i; де i – номер елементу.
.
Значення функції зберегти у векторі F.
|
5 |
0,5+i; 1,5+i; 2,5+i; 3,5+i; 4,5+i.
.
Значення функції зберегти у векторі F.
|
6 |
0; 1,5; 3; 4,5; 6.
.
Значення функції зберегти у векторі F.
|
7 |
6,5; 7,5; 8,5; 9,5; 10,5.
.
Значення функції зберегти у векторі F.
|
8 |
4; 9; 16; 25; 36.
.
Значення функції зберегти у векторі F.
|
9 |
2; 5; 10; 17; 26.
.
Значення функції зберегти у векторі F.
|
10 |
0,5-i; 1,5-i; 2,5-i; 3,5-i; 4,5-i, де i – номер елементу.
.
Значення функції зберегти у векторі F.
|
11 |
0,5; 1,5; 2,5; 3,5; 4,5.
.
Значення функції зберегти у векторі F.
|
12 |
4; 7; 12; 19.
.
Значення функції зберегти у векторі F.
|
13 |
0,5; 3,5; 6,5; 9,5; 12,5.
.
.
|
14 |
1; 1,5; 2; 2,5; 3; 3,5.
.
.
Значення функції зберегти у векторі F.
|
15 |
0,5+i; 1,5+i; 2,5+i; 3,5+i; 4,5+i. (і – номер елементу)
.
.
Значення функції зберегти у векторі F.
|
16 |
i; 1,5+i; 3+i; 4,5+i;,5+i. (і – номер елементу)
.
.
Значення функції зберегти у векторі F.
|
17 |
0,5+i; 1,5+i; 2,5+i; 3,5+i; 4,5+i. (і – номер елементу)
.
.
Значення функції зберегти у векторі F. |
18 |
0,5i; 1,5i; 2,5i; 3,5i; 4,5i. (і – номер елементу)
.
.
Значення функції зберегти у векторі F. |
19 |
0,5+i; 1,5+i; 2,5+i; 3,5+i; 4,5+i.
.
.
Значення функції зберегти у векторі F.
|
20 |
0,5+i; 1,5+i; 2,5+i; 3,5+i; 4,5+i.
.
.
Значення функції зберегти у векторі F.
|
Контрольні питання:
Що таке ранжована змінна?
Для чого використовується ранжована змінна?
Як описується ранжована змінна?
Які основні прийоми обробки векторів і матриць за допомогою ранжованих змінних?
Практична робота №4
Тема: Побудова двомірних графіків в координатних осях X-Y
Завдання практичної роботи:
Ознайомтесь з теоретичними відомостями лекції №10:
побудова двомірних графіків в системі MathCAD
форматування графіків.
Виконайте три індивідуальні завдання. (Варіанти індивідуальних завдань), наведеного нижче.
Короткі теоретичні відомості.
Для створення графіків в системі Mathсad є графічний процесор, який дозволяє будувати найрізноманітніші графіки (у декартовій системі, в полярній системі координат, тривимірні графіки і так далі).
Кожна точка в декартовій системі характеризується своїми координатами X і Y =y(x), де X абсциса точки, а Y ордината. Точки з'єднуються один з одним різноманітними лініями (суцільною, пунктирною і так далі ).
Функція може бути задана як в аналітичному виді (в виді формули) так і в табличному (в виді числових значень)

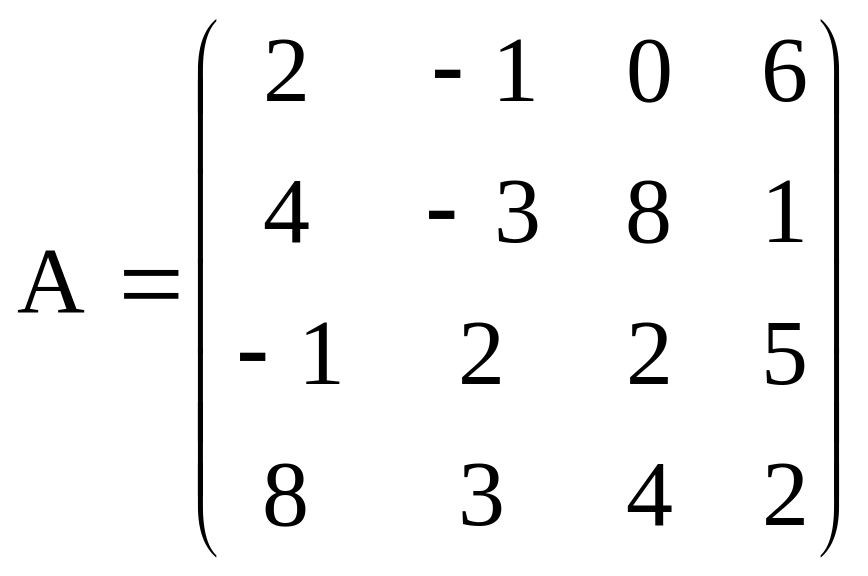 .
. .
. .
. .
. .
. .
.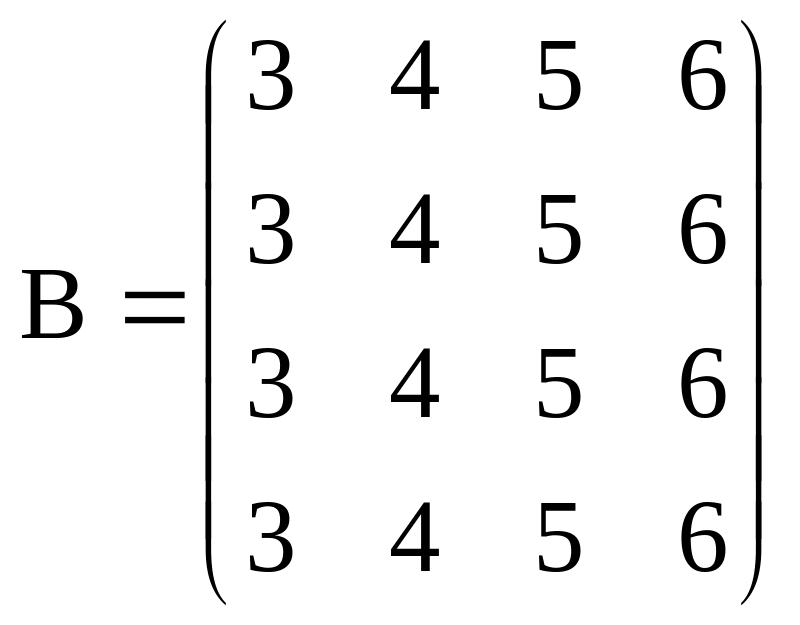 .
. .
. .
.