9.3 Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.

Рассмотрим задачу упрощения уравнения квадрики с использованием ортогональным преобразованием системы координат. Отметим, что при ортогональной замене координат сохраняются метрические характеристики.

Опишем алгоритм приведения квадрики к простейшему виду ортогональным преобразованием.

1. Приводим квадратичную форму к главным осям ортогональным преобразованием . В результате получим уравнение квадрики , где , k – ранг матрицы A, а - ее ненулевые собственные числа.

2. Сдвигом начала координат при и 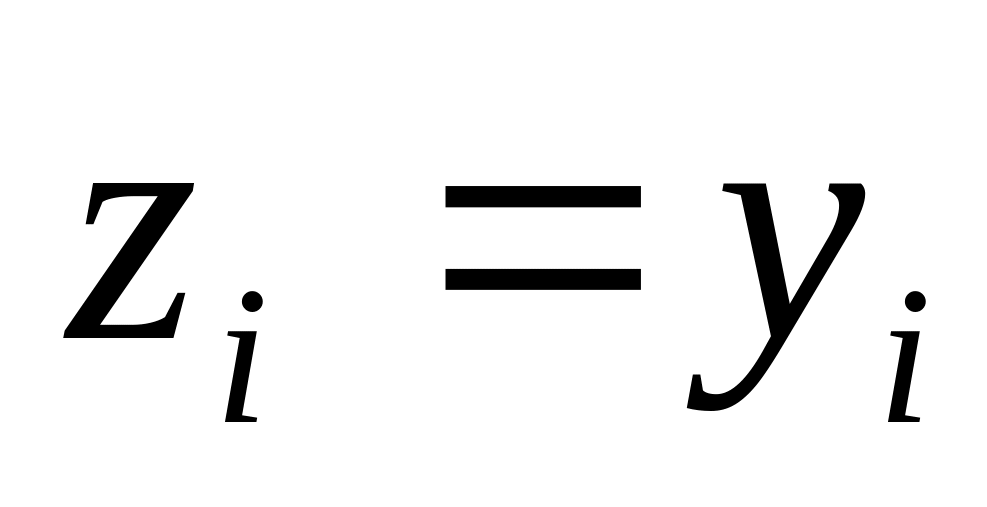при i>k приведем квадрику к виду , где . Если при i>k, то конец, а иначе перейдем на следующий шаг.

3. Положим . Система векторов - ортонормированная. Дополним ее до ортонормированного базиса всего пространства. Пусть T – матрица перехода к новому базису. Сделаем замену переменных . Очевидно, сделанная замена является ортогональной. В новой системе координат уравнение квадрики .

Оформим доказанное выше в виде теоремы.

Теорема 9.36. Ортогональным преобразованием, сдвигом начала координат и умножением на ненулевое число уравнение квадрики приводится к одному из следующих четырех видов , , , .

Обозначим через сумму всех главных миноров k-го порядка матрицы A. Величина является коэффициентом характеристического многочлена при .

Пусть квадрика ортогональным преобразованием x=h+Ty приводится к виду , где , , . Поскольку T ортогональная матрица, то , и, значит, , где k=1,…,n. Кроме того, , и, следовательно, . Тем самым установлен следующий факт.

Свойство 9.26 При ортогональном преобразовании не меняются следующие величины , где k=1,…,n, и , которые называются ортогональными инвариантами квадрики.

К сожалению, ортогональные инварианты не всегда позволяют установить простейший тип квадрики.

Свойство 9.27. Пусть и , тогда не меняется при ортогональном преобразовании.

Доказательство. При ортогональном преобразовании (без сдвига) величины не меняются. Пусть квадратичная форма приводится к главным осям ортогональной заменой координат . Пусть - ортогональное преобразование квадрики. Поскольку , то для доказательства утверждения достаточно рассмотреть случай, когда - диагональная матрица и преобразование заключается в сдвиге на вектор h начала координат. Если , то . В этой матрице единственный минор k порядка, не содержащий нулевых строк, определитель которого не зависит от сдвига. Следовательно, утверждение в данном случае доказано. Пусть , тогда . В этой матрице единственный минор k порядка, не содержащий нулевых строк, определитель которого не зависит от сдвига. Следовательно, утверждение и в данном случае доказано.

Величины называются полуинвариантами ортогонального преобразования.

Набор инвариантов и полуинвариантов квадрики позволяет однозначно установить простейшее уравнение квадрики.

9.4Ортогональная классификация кривых второго порядка

Теорема 9.37. Любая кривая второго порядка ортогонально эквивалентна одному из 9 классов кривых, приведенных в таблице. Приведенные кривые ортогонально не эквивалентны между собой.

Название кривой	Каноническое уравнение кривой
Эллипс
Мнимый эллипс
Гипербола
Пара пересекающихся мнимых прямых
Пара пересекающихся прямых	,
Парабола
Пара параллельных прямых
Пара параллельных мнимых прямых
Пара совпавших параллельных прямых

Доказательство. очевидно