Федеральное государственное бюджетное образовательное учреждение высшего

профессионального образования

САНКТ- ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ

ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ ФАКУЛЬТЕТ

Кафедра «Строительные конструкции и материалы»

Курсовой проект по дисциплине: “ Основы теории надежности ”

Вариант №4

Выполнили: студент гр. 6018/10 Анцулевич Н.А.___________

студент гр. 6018/10 Островский П.Ю.___________

Руководитель: асс. каф. СКиМ Ренев И.А.___________

Санкт-Петербург

2012

1. Расчет показателей надежности резервированных невосстанавливаемых систем

Основным способом повышения надежности и снижения техногенного риска является структурное резервирование, которое реализуется путем введения в систему дополнительных элементов, узлов, блоков.

1.1 Постоянно включенный резерв

Структурная схема системы с постоянно включенным резервом изображена на рис. 1.1.1. Элемент с номером 0 является основным, а элементы с номерами 1,2,..., m — резервными. Общее число элементов в системе n=m+1, где m — кратность резервирования — отношение числа резервных элементов к числу основных.

В данном случае отказ системы наступает при отказе элемента с максималь­ным временем работы, т. е.

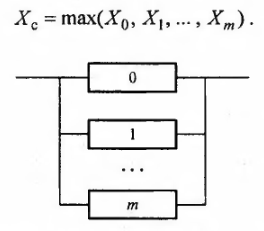
Рис. 1.1.1. Резервированная система с постоянно включенным резервом

Вероятность отказа системы равна произведению веро­ятностей отказов ее элементов:

где - веро­ятность отказа элемента системы.

Если основная система и все резервные одинаковы и имеют вероятность безотказной работы P(t),тогда:

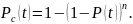
Вероятность безотказной работы системы для случая равнонадежных систем и постоян­ной интенсивности отказов элементов = =...= = определяется по формуле:

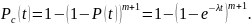
Интенсивность отказов резервированной системы с посто­янно включенным резервом:

Из выражения интенсивности отказов видно, что и с ростом t увеличивается. Пре­дельное значение равно . Зависимость интенсивности отказов от времени приведена на рис. 1.1.2.

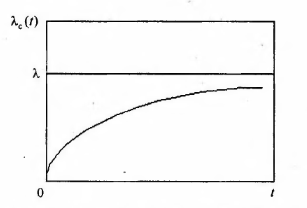
Рис. 1.1.2. Зависимость интенсивности отказа резервированной системы от времени

Среднее время безотказной работы системы:

Так как среднее время безотказной работы нерезервированной системы то

Из формулы видно, что с ростом кратности резервирования среднее время безотказной работы системы растет медленно.

1.2 Резервирование с дробной кратностью

Существуют технические системы, часто называемые мажоритарными, с дробной кратностью резервирования , где m — число резервных элементов, n —общее число элементов.

Мажоритарная система будет работоспособной в течение времени t (собы­тие А) при отказе не более чем m элементов. Пусть — событие, состоя­щее в отказе любых i (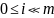 ) элементов за время t. Тогда

Событие произойдет, если откажут любые i элементов, а остальные n-i элементов останутся работоспособными. Вероятность этого события выража­ется формулой Бернулли:

Вероятность безотказной работы мажоритарной системы при условии, что все элементы имеют одинаковую надежность:

При m=0 получаем основное соединение элементов, для которого . При m=n-1 — резервное соединение элементов, для которого . При m=1 получаем систему, отказ которой наступает при отказе двух любых ее элементов. В этом случае .

Рекуррентное соотношение, выражающее вероятность безотказной работы мажоритарной системы через вероятности аналогичной системы меньшей размерности:

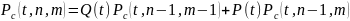
Интенсивность отказа мажоритарной системы:

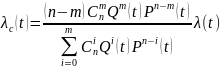
Вычислим, во сколько раз интенсивность отказов системы больше интенсивности отказов одного элемента:

Рассмотрим случай наличия резерва ( ). Тогда в начальный момент времени t=0 получим , а при имеет место равенство:

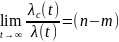
Таким образом, наличие резерва приводит к изменению отношения интенсивности отказов системы к интенсивности отказов элемента от нуля до постоянной величины, равной количеству основных элементов системы (n-m).