Формула Байеса (теорема гипотез)
Пусть известен результат опыта, а именно
то, что произошло событие
.
Этот факт может изменить априорные (то
есть известные до опыта) вероятности
гипотез. Например, в предыдущем примере
извлечение из урны белого шара говорит
о том, что этой урной не могла быть
третья, в которой нет белых шаров, то
есть
.
Для переоценки вероятностей гипотез
при известном результате опыта
используется формула Байеса:
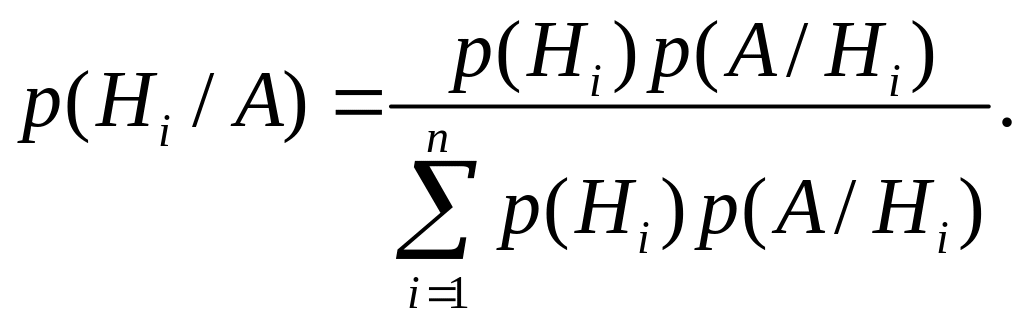
Действительно, из (2.7) получим, что
откуда следует справедливость формулы
(3.2).
Пример. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0.6 и 0.7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.
Решение. Пусть событие – одно попадание при двух выстрелах, а гипотезы:
– первый попал, а второй промахнулся,
– первый промахнулся, а второй попал,
– оба попали,
– оба промахнулись.
Вероятности гипотез:
Тогда
,
.
Следовательно, полная вероятность
.
Применяя формулу Байеса, получим:
Схема повторения испытаний. Формула Бернулли
Рассмотрим серию из
испытаний, в каждом из которых событие
появляется с одной и той же вероятностью
,
причем результат каждого испытания не
зависит от результатов остальных.
Подобная постановка задачи называется
схемой повторения испытаний. Найдем
вероятность того, что в такой серии
событие
произойдет ровно
раз (неважно, в какой последовательности).
Интересующее нас событие представляет
собой сумму равновероятных несовместных
событий, заключающихся в том, что
произошло в некоторых к испытаниях
и не произошло в остальных
испытаниях. Число таких событий равно
числу сочетаний из
по
,
то есть
,
а вероятность каждого из них:
,
где
– вероятность того, что в данном опыте
не произошло. Применяя теорему сложения
для несовместных событий, получим
формулу Бернулли:
Формула справедлива для испытаний Бернулли, т.е. испытаний, удовлетворяющих следующим условиям:
испытания независимые;
в каждом испытании рассматриваются 2 противоположных события: успех и неудача;
вероятность успеха во всех испытаниях одинакова.
Пример. Для получения приза нужно собрать 5 изделий с особым знаком на этикетке. Найти вероятность того, что придется купить 10 изделий, если этикетки с этим знаком имеют 5% изделий.
Решение. Из постановки задачи следует,
что последнее купленное изделие имеет
особый знак. Следовательно, из предыдущих
девяти эти знаки имели 4 изделия. Найдем
вероятность этого по формуле Бернулли:
Тогда
.
Приближение Пуассона для схемы Бернулли
Если вероятность наступления события в каждом испытании постоянна, то вероятность того, что в независимых испытаниях оно состоится раз, при любом числе испытаний определяется формулой Бернулли. Но если число испытаний велико, то вычисления по формуле становятся очень громоздкими.
Например, если вероятность поражения мишени при одном выстреле равна 0.4, то вероятность того, что при 600 выстрелах мишень будет поражена 250 раз, согласно формуле Бернулли:
.
Формально ответ получен. Но нахождение численного значения его даже с помощью таблиц логарифмов связано с серьезными затруднениями. Поэтому, когда число испытаниях велико целесообразно применять другие несложные методы вычисления. Такими формулами являются формулы Муавра-Лапласа и Пуассона.
Локальная теорема Муавра-Лапласа. Если
вероятность
наступления события
в каждом испытании постоянна и отлична
от нуля и единицы, а число испытания
достаточно велико, то вероятность
того, что в
независимых испытаниях событие
наступит
раз, приближенно равна:
,
где функция
определяется равенством:
,
,
.
Формула называется формулой Муавра-Лапласа. Для упрощения расчетов, связанных с применением формулы , составлена таблица значений функции . Пользуясь этой таблицей, необходимо учитывать свойства этой функции:
а) функция
является четной:
.
Поэтому в таблице приведены значения
только для положительных
;
б) функция – монотонно убывающая функция при положительных ;
в) если
,
то можно считать, что
.
Если при большом числе испытаний
вероятность появления
в одном опыте мала, а произведение
сохраняет постоянное значение для
разных серий опытов (то есть среднее
число появлений события А в разных
сериях испытаний остается неизменным),
тогда справедлива формула Пуассона
позволяет найти вероятность к появлений события А для массовых ( велико) и редких ( мало) событий.