
- •080100.62 «Экономика»
- •Пояснительная записка
- •Методические рекомендации по выполнению заданий контрольной работы
- •Тема 1.
- •Алгебра событий
- •Классическое определение вероятности
- •Относительная частота. Статистическое определение вероятности
- •Основные формулы комбинаторики
- •Рекомендации к решению и оформлению задач по данной теме
- •Тема 2.
- •Теорема сложения вероятностей
- •Теорема умножения вероятностей
- •Вероятность появления хотя бы одного события
- •Геометрическая вероятность
- •Рекомендации к решению и оформлению задач по данной теме
- •Тема 3.
- •Формула полной вероятности
- •Формула Байеса (теорема гипотез)
- •Приближение Пуассона для схемы Бернулли
- •Рекомендации к решению и оформлению задач по данной теме
- •Тема 4.
- •Дискретные случайные величины
- •Распределения дискретной случайной величины
- •Тема 5.
- •Экспоненциальное распределение
- •Тема 6.
- •Математическое ожидание.
- •1. Биномиальное распределение.
- •2. Закон Пуассона.
- •3. Равномерное распределение.
- •4. Нормальное распределение.
- •Тема 7.
- •Задания контрольной работы по дисциплине «Теория вероятностей и математическая статистика» Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Вариант № 9
- •Вариант № 10
- •Литература
Вариант № 7
По линии связи передается цифровой текст. В силу характера передаваемой информации и свойств языка, с которого эта информация кодируется цифрами, вероятности
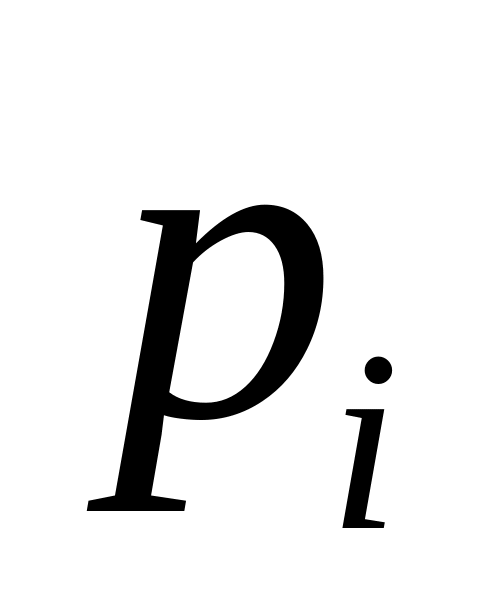 появления в принимаемом тексте отдельных
цифр
появления в принимаемом тексте отдельных
цифр
 различны. Искажения отдельных цифр в
канале связи под действием помех
являются независимыми событиями. Их
вероятности
различны. Искажения отдельных цифр в
канале связи под действием помех
являются независимыми событиями. Их
вероятности
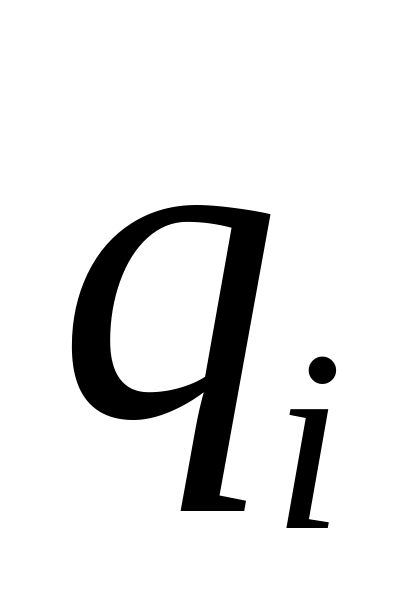 неодинаковы. Найти вероятность
неискаженного приема «слова» из
цифр.
неодинаковы. Найти вероятность
неискаженного приема «слова» из
цифр.В ящике находится 10 карточек с различными номерами. Из ящика по очереди наугад вынимается с возвращением 3 карточки. Какова вероятность, что у них будут разные номера?
В барабане револьвера 7 гнёзд и вставлено 5 патронов. Дважды барабан наугад прокручивается, и каждый раз нажимается курок. Какова вероятность, что выстрела не будет?
Пусть вероятность того, что денежный автомат при опускании одной монеты сработает правильно, равна 0,95. Оценить вероятность того, что при 2 500 опусканиях монет количество случаев правильной работы автомата отклонится (по абсолютной величине) от вероятности 0,95 не более чем на 0,02.
Вероятность попадания в цель при одном выстреле из орудия равна 0,4. Производится шесть выстрелов. Составить закон распределения числа попаданий. Найти математическое ожидание и дисперсию случайной величины.
Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2; второй – 0,3; третий – 0,4. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент услышит радиста хотя бы один раз.
У рыбака имеется три излюбленных места для ловли рыбы, которые он посещает с равной вероятностью каждое. Если он закидывает удочку на первом месте, то клюет с вероятностью ; на втором месте – с вероятностью ; на третьем – с вероятностью . Известно, что рыбак выйдя на рыбалку, три раза закинул удочку и рыба клюнула три раза. Найти вероятность того, что он удил рыбу на первом месте.
Пусть вероятность нарушения герметичности банки консервов равна 0,0005. Найти вероятность того, что среди 2 000 банок две окажутся с нарушением герметичности.
Вероятность попадания в цель
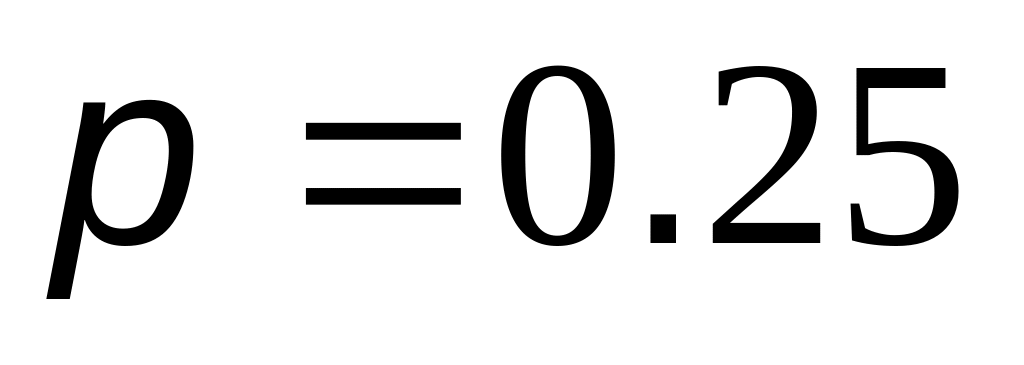 .
Сбрасывается одиночно 8 бомб. Найти
вероятность того, что будет не менее
одного попадания.
.
Сбрасывается одиночно 8 бомб. Найти
вероятность того, что будет не менее
одного попадания.Что вероятнее: выиграть в шахматы по крайней мере три партии из четырех или пять из восьми без ничьих (у равносильного противника)?
Вариант № 8
Группа студентов состоит из отличников, хорошо успевающих и слабо успевающих. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность события ={студент получит хорошую или отличную оценку}.
В студенческой лотерее на 100 билетов приходится 5 денежных и 5 вещевых выигрышей. Студент приобрёл 2 билета. Какова вероятность, что он выиграл и вещь и деньги?
Для оповещения об аварии установлено два сигнализатора, работающих независимо. Первый срабатывает на аварию с вероятностью 0.9, а второй – с вероятностью 0.8. Найти вероятность того, что при аварии сработает хотя бы один сигнализатор.
Сколько следует проверить деталей, чтобы с вероятностью, не меньшей 0,98, можно было ожидать, что абсолютная величина отклонения количества годных деталей от вероятности детали быть годной, равной 0,95, не превысит 0,01 (применить неравенство Чебышева)?
Вероятность попадания в цель при одном выстреле из орудия равна 0,4. Производится шесть выстрелов. Составить закон распределения числа промахов. Найти математическое ожидание и дисперсию случайной величины.
В механизм входят три одинаковые детали. Работа механизма нарушается, если при его сборке будут поставлены все три детали размера, больше обозначенного на чертеже. У сборщика пять деталей их 12 большего размера. Найти вероятность того, что механизм будет работать ненормально, если сборщик берет деталь наугад.
Пассажир может обратиться за получением балета в одну из трех касс. Вероятности обращения в каждую кассу зависят от их местоположения и равны соответственно
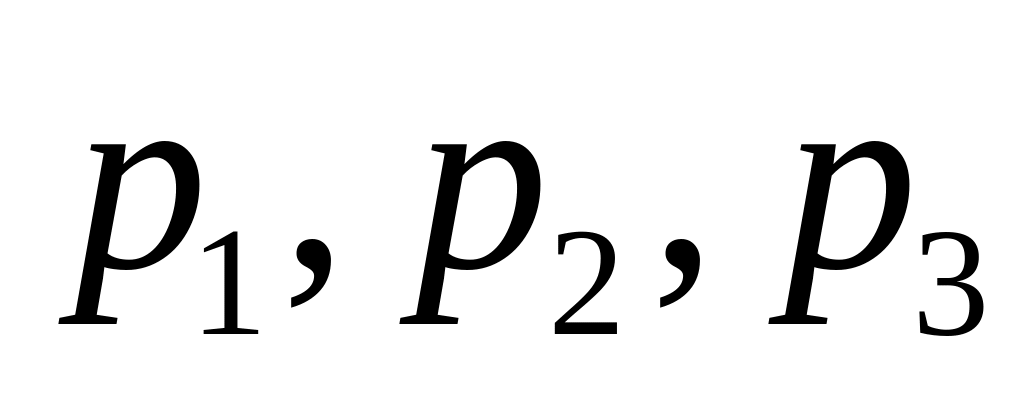 .
Вероятность того, что к моменту прихода
пассажира имеющиеся в кассе билеты
будут распроданы, равна для первой
кассы
.
Вероятность того, что к моменту прихода
пассажира имеющиеся в кассе билеты
будут распроданы, равна для первой
кассы
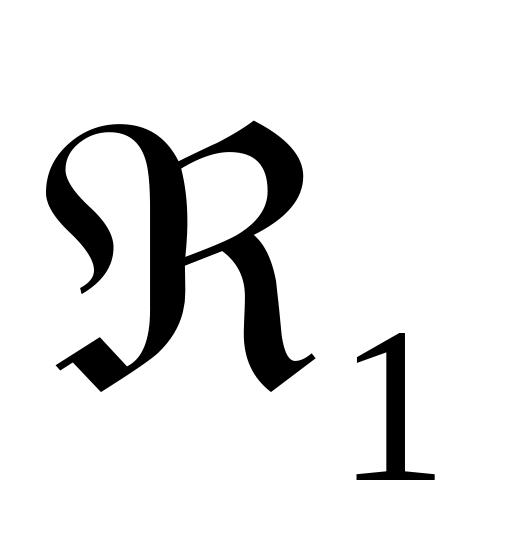 ,
для второй –
,
для второй –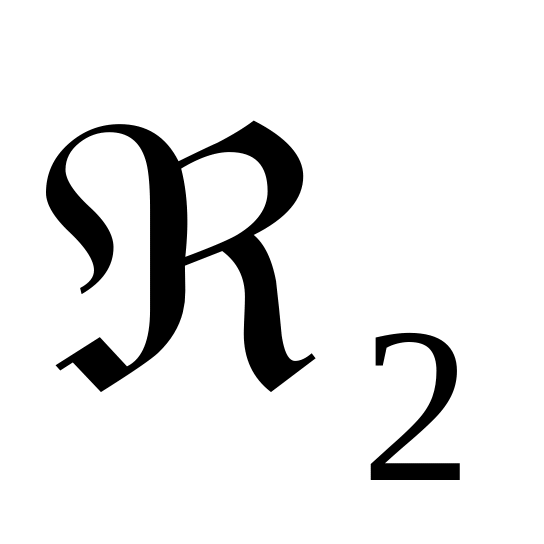 ,
для третьей –
,
для третьей –
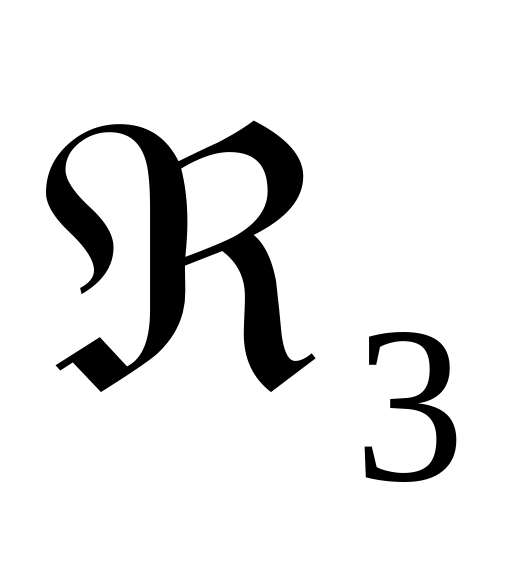 .
Пассажир направился за билетом в одну
из касс и купил билет. Найти вероятность
того, что это была первая касса.
.
Пассажир направился за билетом в одну
из касс и купил билет. Найти вероятность
того, что это была первая касса.Вероятность неточной сборки прибора равна 0,2. Найти вероятность того, что среди 500 приборов окажется от 410 до 430 (включительно) точных.
Человек, принадлежащий к определенной группе населения с вероятностью 0,2 оказывается брюнетом, с вероятностью 0,3 – шатеном, с вероятностью 0,4 – блондином и с вероятностью 0,1 – рыжим. Выбирается наугад группа из 6 человек. Найти вероятность того, что а) в составе группы равное число блондинов и шатенов; б) в составе группы нет ни одного рыжего.
Вероятность попадания в цель . Сбрасывается одиночно 8 бомб. Найти вероятность того, что будет не менее 7 попаданий.
