Вариант № 5

1. В трех урнах имеются белые и черные шары. В первой урне – 8 белых и один черный шар, во второй – 6 белых и 4 черных, в третьей – 9 белых и один черный. Из наугад выбранной урны случайным образом вынимается шар. Найти вероятность того, что он белый.

2. Среди 17 студентов группы, из которых восемь девушек, разыгрывается семь билетов, причем каждый может выиграть только один билет. Найти вероятность того, что среди обладателей билетов окажутся четыре девушки. Решить, пользуясь лишь определением вероятности.

3. Из урны, содержащей белых и черных шаров, последовательно вынимают два шара, но после первого вынимания шар возвращают в урну, и шары в урне перемешивают. Найти вероятность того, что оба шара окажутся белыми.

4. Количество воды, необходимое предприятию в течение суток для технических нужд, является случайной величиной, математическое ожидание которой равно 85 м³, а среднее квадратическое отклонение – 15 м³. Почему нельзя применить неравенство Чебышева для оценки вероятности того, что в ближайшие сутки расход воды составит от 60 м³ до 100 м³? Как нужно изменить правую границу, чтобы применение неравенства Чебышева стало возможным? Решить задачу при соответствующем изменении правой границы.

5. В круг радиуса наудачу бросается точка. Найти функцию распределения и плотность распределения расстояния этой точки от центра круга. Найти математическое ожидание и дисперсию.

6. При приеме партии изделий подвергается проверке половина изделий. Условие приемки – наличие брака в выборке менее 2%. Найти вероятность того, что партия из 100 изделий, содержащая 5% брака, не будет принята.

7. При обследовании больного имеется подозрение на одно из двух заболеваний и . Их вероятности в данных условиях: 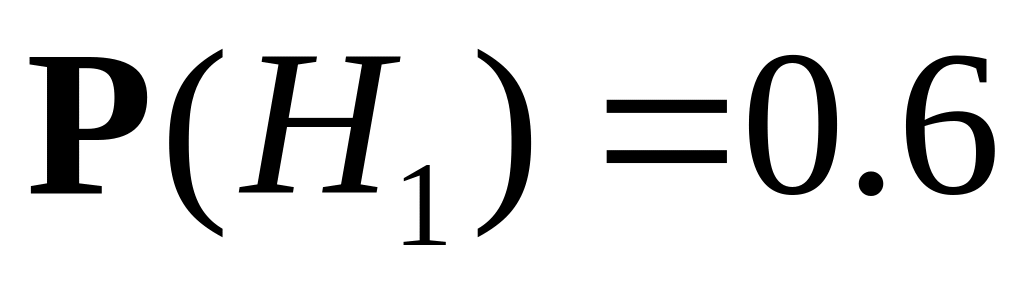, . Для уточнения диагноза назначается анализ, результатом которого является положительная или отрицательная реакция. В случае болезни вероятность положительной реакции равна 0.9, отрицательной – 0.1; в случае положительная и отрицательная реакции равновероятны. Анализ произвели дважды, и оба раза реакция оказалась отрицательной (событие ). Требуется найти вероятность каждого заболевания после проделанных анализов.

8. Вероятность рождения мальчика равна 0,515. Найти вероятность того, что среди 1 000 новорожденных будет 480 девочек.

9. Пусть вероятность того, что компьютер потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из шести компьютеров хотя бы один потребует ремонта.

10. При передаче сообщения вероятность искажения одного знака равна 0.1. Каковы вероятности того, что сообщение из 10 знаков содержит не более 3-х искажений.

Вариант № 6

1. Группа студентов состоит из отличников, хорошо успевающих и слабо успевающих. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад три студента. Найти вероятность того, что они получат отметки: отлично, хорошо, удовлетворительно (в любом порядке).

2. На девяти карточках написаны цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8. Две из них вынимаются наугад и укладываются на стол в порядке появления, затем читается полученное число, например 07 (семь), 14 (четырнадцать) и т.п. Найти вероятность того, что число будет четным.

3. Студент пришёл на экзамен, зная лишь 20 вопросов из 25-ти. Преподаватель наугад дал 2 вопроса. Какова вероятность, что студент получил вопросы, которые он выучил?

4. Вероятность изготовления детали с дефектами равна 0,8. Почему нельзя применить неравенство Чебышева для оценки вероятности того, что доля дефектных деталей среди 4 000 изготовленных будет находиться в границах от 0,78 до 0,83 включительно? Решить задачу при соответствующем изменении левой границы.

5. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,5, вторым –0,4. Составить закон распределения числа попаданий в мишень. Найти математическое ожидание и дисперсию случайной величины.

6. Деталь проходит три операции обработки. Вероятность того, что она окажется бракованной после первой операции, равна 0,02; после второй – 0,03; после третьей – 0,02. Найти вероятность того, что деталь будет небракованной после трех операций, предполагая, что появление брака на отдельных операциях независимые события.

7. У рыбака имеется три излюбленных места для ловли рыбы, которые он посещает с равной вероятностью каждое. Если он закидывает удочку на первом месте, то клюет с вероятностью ; на втором месте – с вероятностью ; на третьем – с вероятностью . Известно, что рыбак выйдя на рыбалку, три раза закинул удочку и рыба клюнула только один раз. Найти вероятность того, что он удил рыбу на первом месте.

8. Пусть вероятность нарушения герметичности банки консервов равна 0,0005. Найти вероятность того, что среди 2 000 банок не больше двух окажутся с нарушением герметичности.

9. Прибор имеет шесть ламп, вероятность каждой из которых перегореть при данном повышении напряжения в цепи равна 0.3. При перегорании трех или менее ламп прибор из строя не выходит. при сгорании четырех ламп вероятность выхода прибора из строя равна 0.3, при сгорании пяти ламп – 0.7, при сгорании шести ламп – 1. Определить вероятность выхода прибора из строя при повышении напряжения.

10. Что вероятнее выиграть у равносильного противника: 1) три партии из четырех или пять из восьми; 2) не менее трех партий из четырех или не менее пяти партий из восьми?