Задания контрольной работы по дисциплине «Теория вероятностей и математическая статистика» Вариант № 1

1. Группа студентов состоит из отличников, хорошо успевающих и слабо успевающих. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки, слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад три студента. Найти вероятность того, что они все получат отметки: хорошо.

2. При передаче сообщения вероятность искажения одного знака равна 0.1. Каковы вероятности того, что сообщение из 10 знаков не будет искажено.

3. На пяти карточках написаны цифры: 1, 2, 3, 4, 5. Две из них, одна за другой, вынимаются. Найти вероятность того, что число на второй карточке будет больше, чем на первой.

4. Вероятность опоздания пассажира на поезд равна 0,007. Оценить вероятность того, что из 20 000 будет от 100 до 180 (включительно) опоздавших.

5. Дана плотность вероятности: . Найти постоянную . Найти математическое ожидание и дисперсию случайной величины.

6. Имеется пять винтовок, из которых три с оптическим прицелом. Вероятность попадания в цель при одном выстреле из винтовки с оптическим прицелом равна 0,95, без оптического прицела – 0,8. Найти вероятность попадания в цель, если стрелок сделает выстрел из наудачу взятой винтовки.

7. В тесто объемом 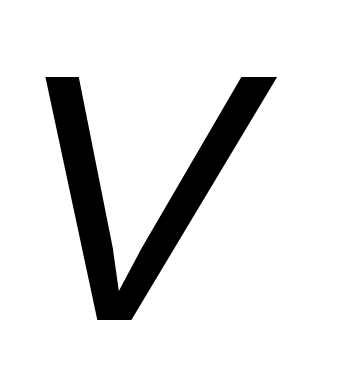бросают 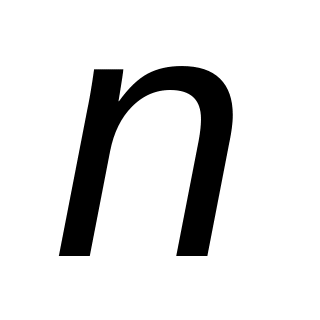изюминок. Тесто перемешивают и разрезают на отдельные булочки объемом 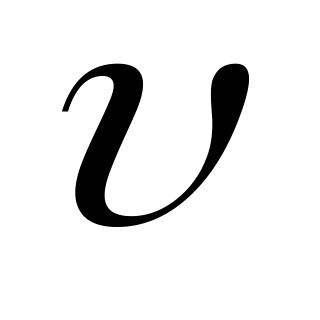. Найти вероятность того, что в булочке будет хотя бы одна изюминка, если , .

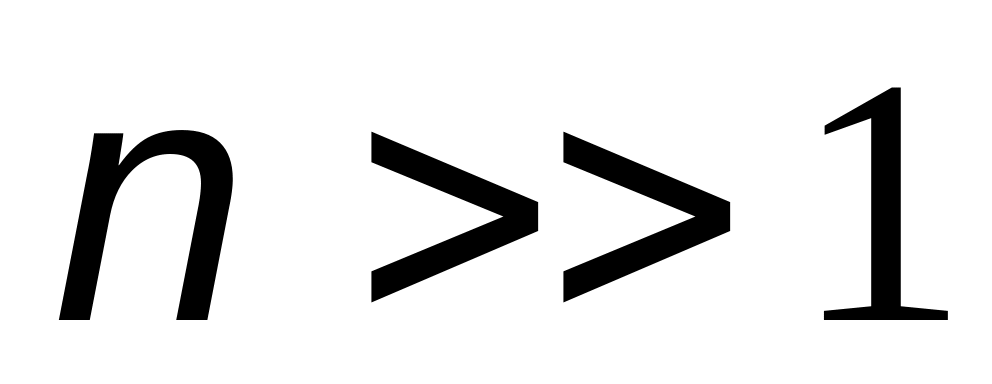8. Пусть вероятность нарушения герметичности банки консервов равна 0,0005. Найти вероятность того, что среди 2 000 банок хотя бы одна окажется с нарушением герметичности.

9. Вероятность того, что наудачу взятая деталь для сборки компьютера, равна 0,1. Найти вероятность того, что среди взятых наудачу пяти деталей не более двух окажутся нестандартными.

10. Вероятность выигрыша по одному билету лотереи равна 1/7. Какова вероятность того, что лицо, имеющее шесть билетов не выиграет по двум билетам.

Вариант № 2

1. Группа студентов состоит из отличников, хорошо успевающих и слабо успевающих. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность того, что студент получит хорошую оценку.

2. Из ящика, содержащего три билета с номерами 1, 2, 3 вынимают по одному все билеты. Предполагается, что все последовательности номеров билетов имеют одинаковые вероятности. Найти вероятность того, что хотя бы у одного билета порядковый номер совпадает с собственным.

3. Два игрока по очереди бросают игральную кость, каждый по одному разу. Выигравшим считается тот, кто получит большее число очков. Найти вероятность выигрыша первого игрока.

4. Вероятность того, что покупателю потребуется мужская обувь 42-го размера, равна 0,25. Оценить вероятность того, что отклонение доли покупателей, которым необходима обувь 42-го размера, от вероятности 0,25 не превзойдет по абсолютной величине 0,06, если ожидается 2500 покупателей.

5. Имеется пять различных ключей, из которых только один подходит к замку. Составить закон распределения числа опробований при открывании замка, если испробованный ключ в последующих попытках открыть замок участвует. Найти математическое ожидание и дисперсию случайной величины.

6. Имеется пять винтовок, из которых три с оптическим прицелом. Вероятность попадания в цель при одном выстреле из винтовки с оптическим прицелом равна 0,95, без оптического прицела – 0,8. Найти вероятность промаха, если стрелок сделает выстрел из наудачу взятой винтовки.

7. В тесто объемом бросают изюминок. Тесто перемешивают и разрезают на отдельные булочки объемом . Найти вероятность того, что в булочке будет 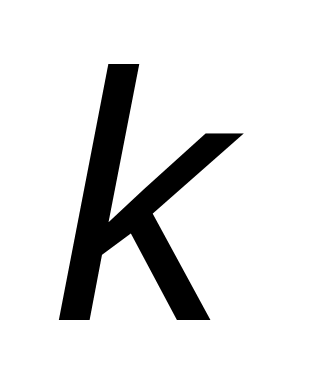изюминок, если , .

8. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из 750 покупателей не более 120 потребуют обувь этого размера.

9. Вероятность выигрыша по одному билету лотереи равна 1/7. Какова вероятность того, что лицо, имеющее шесть билетов не выиграет ни по одному билету.

10. Пусть вероятность того, что компьютер потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из шести компьютеров не более одного потребует ремонта.