Экспоненциальное распределение

Примером вероятностной модели, в которой появляется экспоненциальное распределение, является пуассоновский поток событий. Экспоненциально распределенным в этом случае оказывается время ожидания  очередного события.

Плотность экспоненциального распределения имеет вид:

Здесь имеет смысл интенсивности потока (среднее число событий в единицу времени). Важным частным примером экспоненциальной случайной величины является длина свободного пробега ионизирующей частицы в однородном веществе. В этом случае - макроскопическое сечение взаимодействия (вероятность взаимодействия частицы на единице длины пути).

В отличие от нормального распределения, показательный закон определяется только одним параметром . В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно. Понятно, что оценить один параметр проще, чем несколько.

Найдем функцию распределения показательного закона:

Следовательно,

Теперь можно найти вероятность попадания показательно распределенной случайной величины в интервал :

Пример. Пусть время безотказной работы элемента распределено по показательному закону с плотностью распределения при . Найти вероятность того, что элемент проработает безотказно в течение 10 часов.

Решение. Так как ,

Нормальное распределение.

7. Нормальное распределение – самое распространенное в приложениях. Нормальное распределение, как правило, имеют случайные величины, складывающиеся из большого числа слабо связанных малых случайных величин.

Плотность нормального распределения имеет колоколообразный вид:

,

где - положение максимума колокола, - точки перегиба.

Замечание. Таким образом, нормальное распределение определяется двумя параметрами: и .

1. График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Примерный вид кривой Гаусса изображен на рис.1.

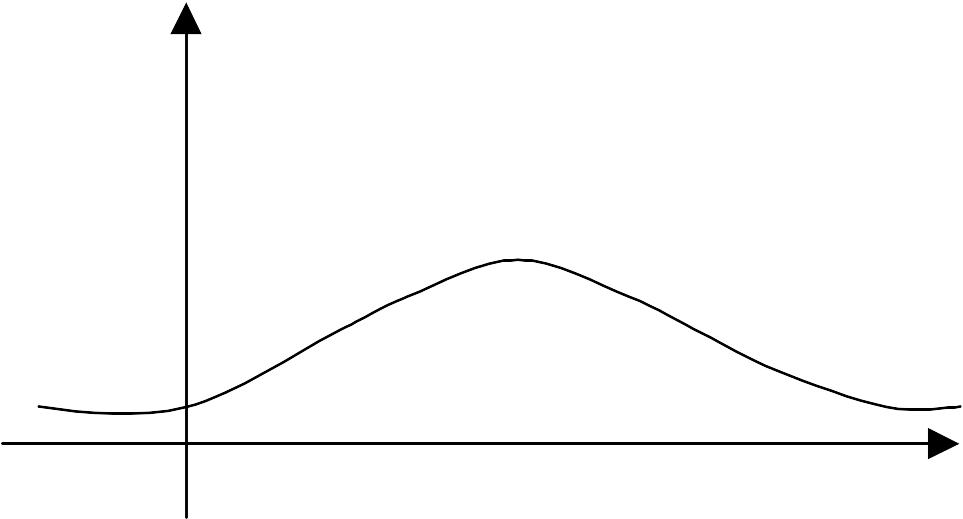
Рис.1.

Найдем вид функции распределения для нормального закона:

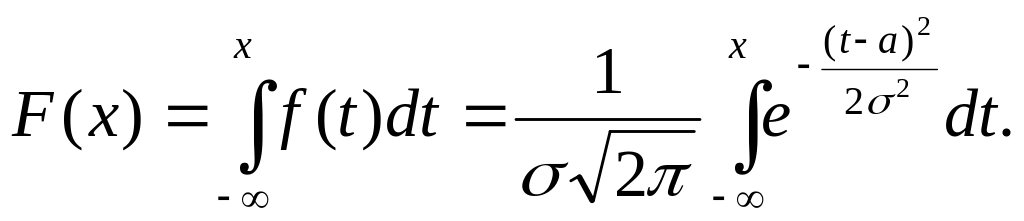
Перед нами так называемый «неберущийся» интеграл, который невозможно выразить через элементарные функции. Поэтому для вычисления значений F(x) приходится пользоваться таблицами. Они составлены для случая, когда , а .

Определение 6.2. Нормальное распределение с параметрами , называется нормированным, а его функция распределения

называется функцией Лапласа.

Замечание. Функцию распределения для произвольных параметров можно выразить через функцию Лапласа, если сделать замену: , тогда .

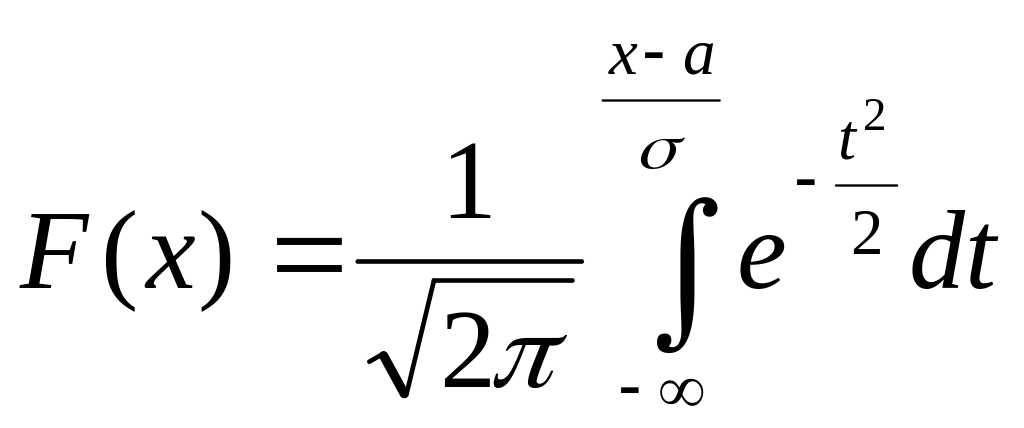Найдем вероятность попадания нормально распределенной случайной величины на заданный интервал:

Пример. Случайная величина имеет нормальное распределение с параметрами . Найти вероятность того, что она примет значение из интервала (4, 8).

Решение.

Правило «трех сигм».

Найдем вероятность того, что нормально распределенная случайная величина примет значение из интервала

Следовательно, вероятность того, что значение случайной величины окажется вне этого интервала, равна 0,0027, то есть составляет 0,27% и может считаться пренебрежимо малой. Таким образом, на практике можно считать, что все возможные значения нормально распределенной случайной величины лежат в интервале

Полученный результат позволяет сформулировать правило «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от не превосходит 3σ.