3.4.Собственные числа и собственные векторы матрицы

Приведем основные определения и теоремы, необходимые для решения практических задач вычисления собственных чисел и собственных векторов матриц.

Определение 3.5. Собственным числом (или собственным значением) квадратной матрицы A называется число λ такое, что система уравнений

Ax = λx (3.35)

имеет ненулевое решение x. Это решение называется собственным вектором матрицы A, соответствующим собственному значению λ.

Собственный вектор определяется с точностью до постоянного множителя, — если x удовлетворяет (3.35), то и cx также является решением (3.35).

Преобразуем систему (3.35) к виду (A – λE)x = 0, где E — единичная матрица. Так как система линейных однородных уравнений имеет ненулевые решения лишь тогда, когда определитель матрицы равен нулю, получим уравнение для определения собственных значений

det(A – λE) = 0, (3.36)

которое называется характеристическим или вековым уравнением.

Если раскрыть определитель, то получим в левой части (3.36) многочлен n-й степени, корнями которого являются собственные значения матрицы A. На практике, при больших порядках n матрицы, задача раскрытия определителя (3.36) является сложной. Как известно из алгебры, многочлен n-й степени имеет n корней (действительных или комплексных), если кратные корни учитывать столько раз, какова их кратность.

Пример 3.9. Найти собственные значения и собственные векторы матрицы

.

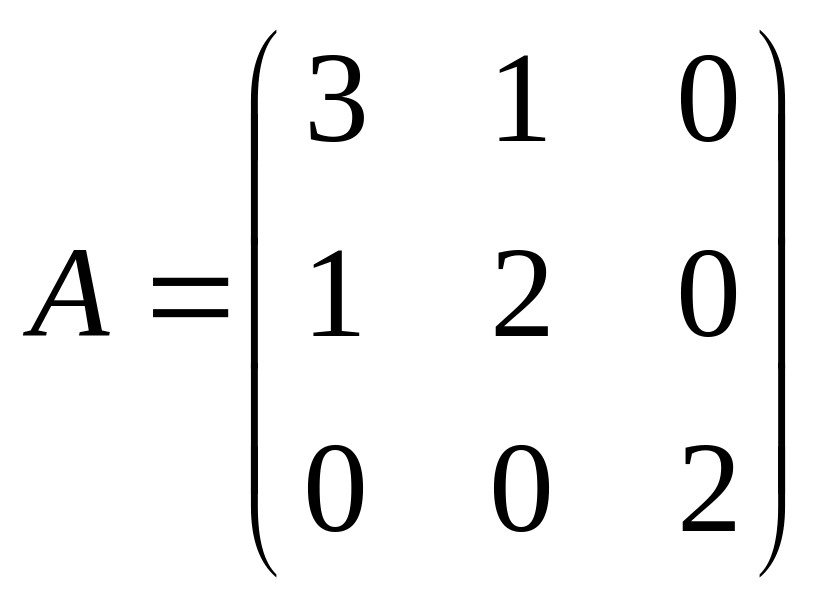Решение. Составим характеристическое уравнение и решим его:

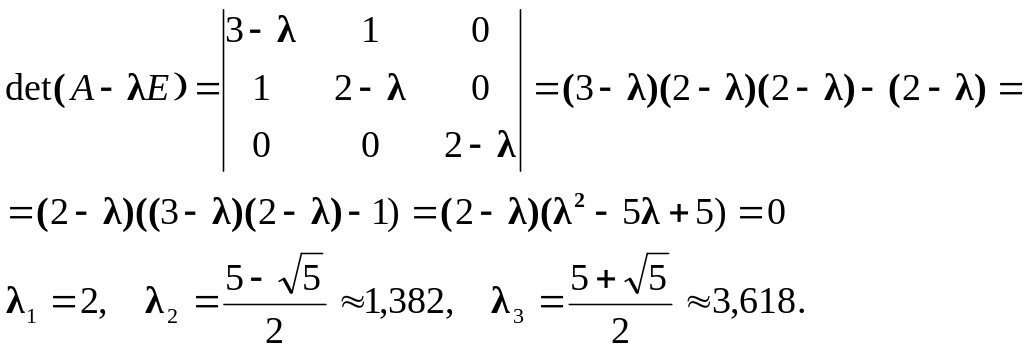
Найдем собственные векторы, решая системы уравнений.

Отсюда следует, что x₃ — произвольное число. Выберем x₃ = 1, тогда получим собственный вектор x¹ = (0, 0, 1)^T, соответствующий собственному значению λ₁ = 2.

Первое и второе уравнения оказались одинаковыми, мы получили одно уравнение с двумя неизвестными. Пусть x₂ = 1, тогда x₁ = –0,618 и второй собственный вектор равен x² = (–0,618; 1; 0)^T.

Аналогично предыдущему, пусть x₁ = 1, тогда x₂ = 0,618 и третий собственный вектор равен x³ = (1; 0,618; 0)^T.

Нормируем найденные векторы, т.е. разделим каждый вектор на его длину:

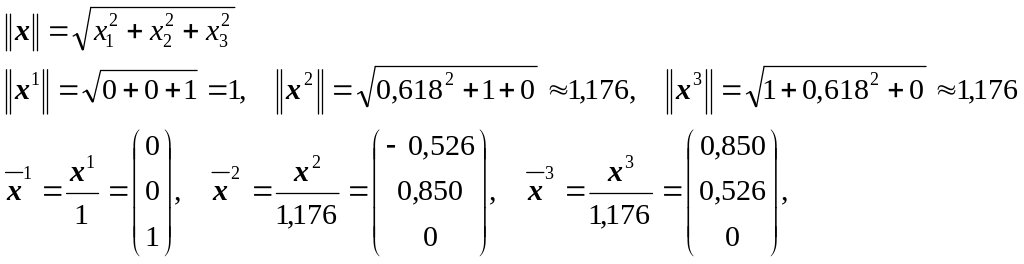
Правильность вычислений можно проверить в программе Mathcad с помощью функций eigenvals(A) и eigenvecs(A):

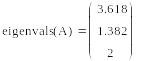
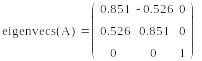
Как видим, результаты ручного расчета практически совпадают со значениями, полученными в программе Mathcad.

Проверьте самостоятельно, что найденные собственные векторы взаимно ортогональны, т.е. при i ≠ k равно нулю скалярное произведение .

Вычислить собственные значения матрицы в общем случае труднее, чем найти при известных собственных значениях соответствующие собственные векторы. В некоторых частных случаях собственные значения вычисляются легко. Например, если матрица диагональная или треугольная, то определитель равен произведению диагональных элементов и поэтому собственные значения равны диагональным элементам. Нетрудно вычислить собственные значения для трехдиагональной матрицы, а также для почти треугольной матрицы.

Для диагональной матрицы собственному значению λ_i = a_ii отвечает единичный собственный вектор xⁱ = (0, …, 1, …,0)^T, у которого i-я компонента равна 1, а остальные компоненты равны 0.

Теорема 3.5. Собственные значения симметричной матрицы с действительными элементами действительны, а собственные векторы, соответствующие различным собственным значениям, взаимно ортогональны.

Теорема 3.6. Если λ_min и λ_max — наименьшее и наибольшее собственные значения действительной симметричной матрицы A, то для любого вектора x справедливо неравенство

λ_min(x, x) ≤ (Ax, x) ≤ λ_max(x, x) (3.37)

Определение 3.6. Действительная симметричная матрица A называется положительно определенной, если для любого вектора x ≠ 0 выполняется условие

(Ax, x) > 0 (3.38)

Теорема 3.7. Действительная симметричная матрица A является положительно определенной тогда и только тогда, когда все её собственные значения положительны.

Теорема 3.8 (критерий Сильвестра). Для того чтобы действительная симметричная матрица A = [a_ij] была положительно определенной необходимо и достаточно, чтобы все главные диагональные миноры её определителя были положительны:

(3.39)

Теорема 3.9 (теорема Перрона). Если все элементы квадратной матрицы положительны, то её наибольшее по модулю собственное значение положительно и не является кратным, а соответствующий собственный вектор имеет положительные координаты.

Рассмотрим итерационный метод определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы A, который запишем в виде следующего алгоритма [7]:

Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами.

1. Зададим начальное приближение x⁰ к собственному вектору; k = 0;

2. Вычисляем следующие приближения x^k+1 формулам

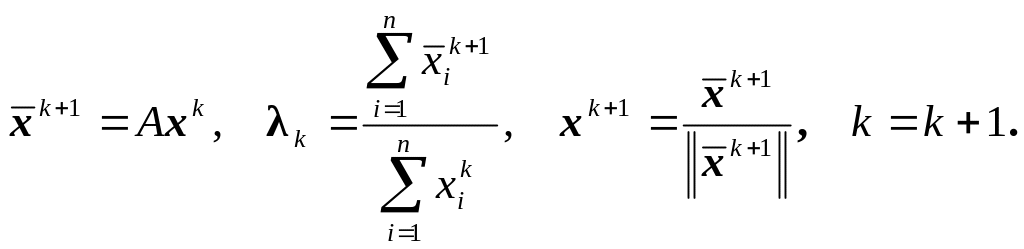(3.40)

3. Если |λ_k+1 – λ_k| ≥ ε, переходим к пункту 2, иначе — к 4;

4. Конец.

Критерием для остановки итераций является условие |λ_k+1 – λ_k| < ε, где ε — заданная погрешность.

В (3.40) можно вычислить сначала k-ю степень матрицы A и умножить её на вектор x⁰ (см. пример 3.10), а в формуле для λ_k можно брать отношение ненулевой координаты вектора x^k+1 к соответствующей координате вектора x^k, которая тоже не должна быть равной нулю. Так как заранее не известно, какие координаты собственного вектора не равны нулю, то лучше брать отношение сумм координат.

Пример 3.10. Найти наибольшее по модулю собственное значение и соответствующий собственный вектор матрицы A из примера 3.9.

Решение. Проведем расчеты в программе Mathcad. Вычислим x¹⁰ = A¹⁰∙x⁰ и x¹¹ = A¹¹∙x⁰ и найдем собственное значение как отношение сумм координат векторов x¹¹ и x¹⁰, а затем нормируем x¹¹:

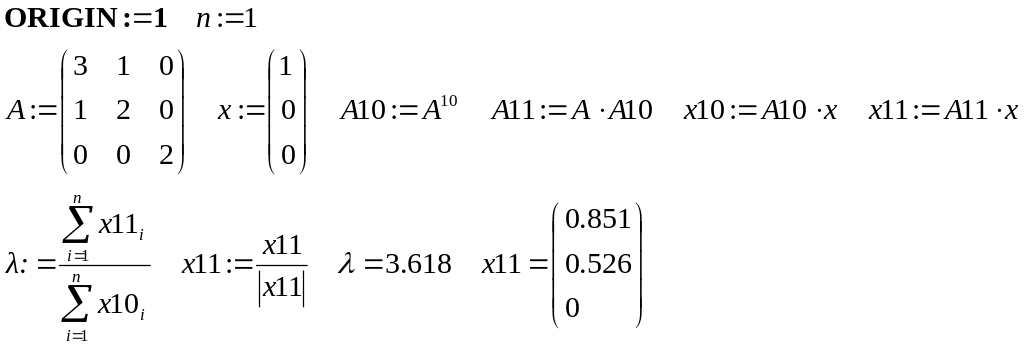
Полученные результаты практически совпадают с решением предыдущего примера 3.9.

Составим на C++ программу вычисления наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы A по формулам (3.40):

#include <iostream.h>

#include <except.h>

#include <math.h>

int EigenMax(long double **a, long double *eig_val,long double *x0,

long double *x1, long double eps, const int n, int k_max);

int main(){

long double **a, *x0, *x1, eigv, eps; int i,j,n,k_max;

cout <<"\n input n = " ; cin >> n;

cout <<"\n input k_max = " ; cin >> k_max;

cout <<"\n input eps = " ; cin >> eps;

try {

a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n];

x0= new long double[n]; x1= new long double[n];

}

catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);}

cout <<"\n input matrix a \n";

for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j];

for (i=0; i<n; i++){cout << "\n";for (j=0; j<n; j++)cout <<" "<< a[i][j];}

cout <<"\n input vector x0\n";

for (i=0; i<n; i++)cin >> x0[i];

for (i=0; i<n; i++)cout << "\n x0[" << i <<"] =" << x0[i];

eigv = 0;

EigenMax(a, &eigv, x0, x1,eps, n, k_max);

cout << "\n Max Eigen Value = " << eigv;

cout << "\n Eigen Vector: " ;

for (i=0; i<n; i++)cout << "\n x1[" << i <<"] =" << x1[i];

cin >> i; // for pause

for(i = 0; i < n; i++) delete[] a[i];

delete a;

delete[] x0;

delete[] x1;

return 0;

}//end main

int EigenMax(long double **a, long double *eig_val,long double *x0,

long double *x1, long double eps, const int n, int k_max){

int i, j, k; long double xerr, xnrm, eig0, s, s0, s1;

k = 0;

do { eig0 = *eig_val;

for (i = 0; i < n; i++){

s = 0; for (j = 0; j < n; j++)s += a[i][j]*x0[j]; x1[i] = s;}

s0 = 0; s1 = 0;

for (i = 0; i < n; i++){s0 += x0[i]; s1 += x1[i];}

*eig_val = s1/s0; xerr = fabs(*eig_val - eig0);

xnrm = 0;

for (i = 0; i <= n-1; i++) xnrm += x1[i]*x1[i];

xnrm = sqrt(xnrm);

for (i = 0; i < n; i++){x1[i] = x1[i]/xnrm; x0[i] = x1[i]; }

k = k + 1; if (k > k_max)break;

}while (xerr > eps);

return 0;

}// end EigenMax

Найдем с помощью этой программы наибольшее собственное значение матрицы из примера 3.10:

Input n = 3

Input k_max = 1000

Input eps = 0.000001

Input matrix a

3 1 0 1 2 0 0 0 2

3 1 0

1 2 0

0 0 2

Input vector x0

3

2

1

Max Eigen Value = 3.61795

Eigen Vector:

x1[0] =0.850651

x1[1] =0.525731

x1[2] =3.81633e–05

Результаты с заданной точностью совпадают со значениями, найденными в примерах 3.9, 3.10.