
- •3.Вычислительные методы линейной алгебры
- •3.1.Нормы векторов и матриц
- •3.2.Решение систем линейных алгебраических уравнений
- •3.2.1.Метод Гаусса для решения систем линейных уравнений
- •3.2.2.Итерационный метод
- •3.2.3.Метод Зейделя
- •3.2.4.Погрешность решения и обусловленность системы уравнений
- •3.3.Вычисление определителя и обратной матрицы
- •3.4.Собственные числа и собственные векторы матрицы
- •3.4.1.Метод скалярных произведений
- •3.4.2.Вычисление всех собственных значений положительно определенной симметричной матрицы
3.Вычислительные методы линейной алгебры
Вычислительные методы линейной алгебры изучают численные методы решения следующих задач:
1) Решить систему линейных алгебраических уравнений (СЛАУ).
2) Вычислить определитель квадратной матрицы A.
3) Для данной квадратной матрицы A найти обратную A–1.
4) Определить собственные значения и собственные векторы квадратной матрицы A.
3.1.Нормы векторов и матриц
Приведем определения норм векторов и матриц [1]. Пусть задан вектор x = (x1, x2, …, xn)T. Наиболее часто для векторов используются следующие нормы:
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
![]() (3.3)
(3.3)
Норма (3.3) порождена скалярным произведением векторов
![]() .
.
Для скалярного произведения справедливы следующие соотношения:
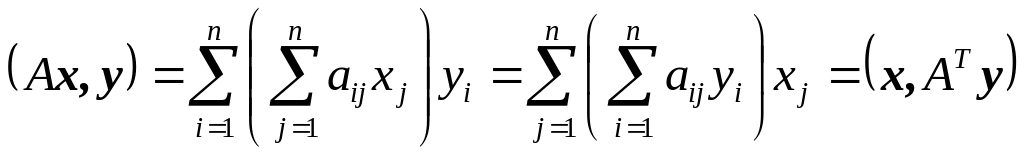 .
.
Если A симметричная матрица, то (Ax, y) = (x, Ay).
Определение 3.1. Нормой матрицы A называется число
![]() .
(3.4)
.
(3.4)
Согласованные с нормами векторов (3.1) — (3.3) нормы матриц определяются формулами
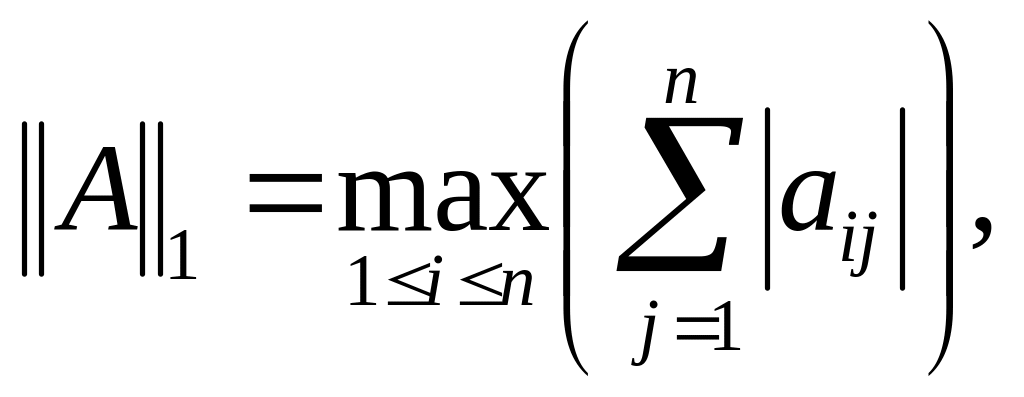 (3.5)
(3.5)
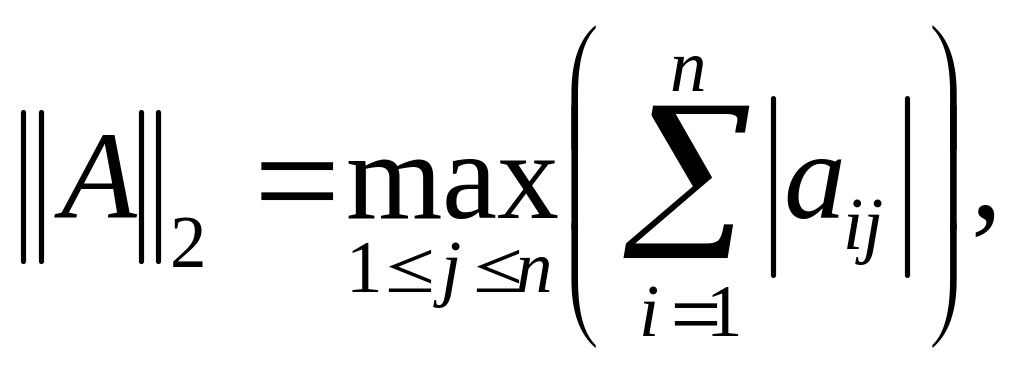 (3.6)
(3.6)
![]() (3.7)
(3.7)
Здесь
![]() — собственные значения матрицы ATA,
которая является симметричной. Чтобы
обосновать формулу (3.7)
рассмотрим определение нормы матрицы
(3.4):
— собственные значения матрицы ATA,
которая является симметричной. Чтобы
обосновать формулу (3.7)
рассмотрим определение нормы матрицы
(3.4):
![]()
Можно доказать [1], что для симметричной матрицы B верно соотношение
![]() ,
(3.8)
,
(3.8)
где λi — собственные значения матрицы B. Отсюда следует формула (3.7).
Пример 3.1. Вычислить нормы ||x||1, ||x||2, ||x||3 вектора x = (1, 2, – 3)T.
Решение. Пользуясь определениями норм (3.1) — (3.3), вычислим
![]()
![]()
![]()
Пример 3.2. Вычислить нормы ||A||1, ||A||2, ||A||3 матрицы
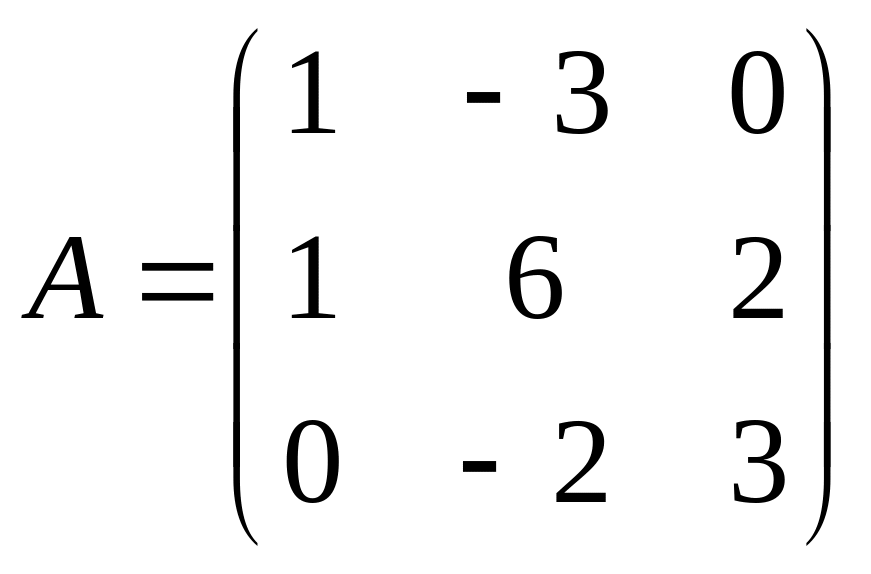
Решение. По формулам (3.5), (3.6) находим нормы матриц
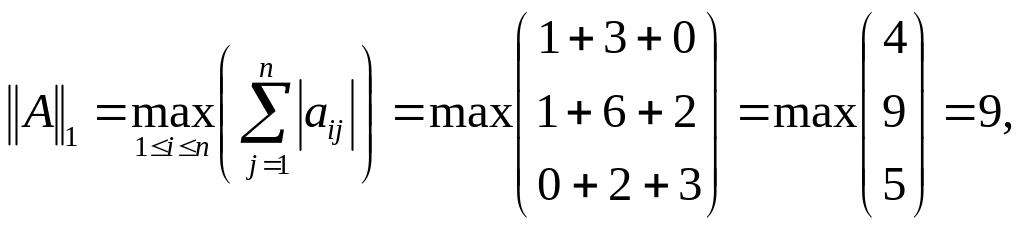
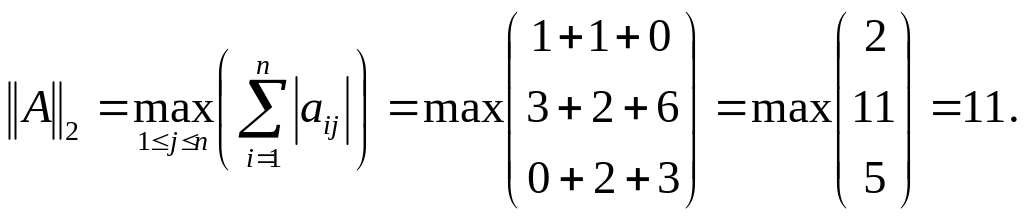
Чтобы вычислить норму матрицы по формуле (3.7) необходимо найти собственные значения матрицы, полученной умножением транспонированной матрицы AT на данную матрицу A:
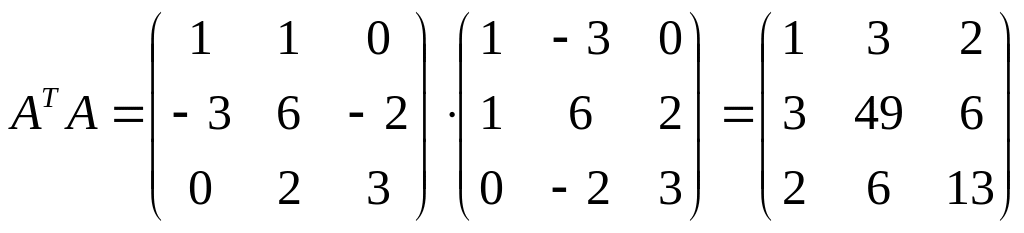 .
.
Не вдаваясь пока в подробности методов вычисления собственных значений матриц, вычислим в программе Mathcad собственные значения матрицы с помощью функции eigenvals:
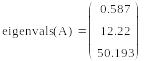
Теперь мы можем вычислить норму матрицы по формуле (3.7):
![]()
Определение 3.2. Две нормы ||x||α и ||x||β называются эквивалентными, если существуют постоянные γ1 и γ2 такие, что при всех x ≠ 0 справедливы соотношения
||x||α/||x||β ≤ γ1, ||x||β /||x||α ≤ γ2.
Нормы ||x||1, ||x||2, ||x||3 эквивалентны между собой, так как выполняются неравенства [1]
||x||1 ≤ ||x||3 ≤ ||x||2 ≤ n||x||1.
Из эквивалентности норм ||x||1, ||x||2, ||x||3 следует, что, если последовательность векторов сходится по одной из этих норм, то она сходится и по остальным нормам.
Ниже мы будем подразумевать под нормой ||x|| одну из указанных норм, а при необходимости конкретизировать, какую именно. При этом будем под нормой матрицы подразумевать норму, согласованную с нормой вектора.
